Cho prôtôn có động năng K_p = 2,5 MeV bắn phá hạt nhân \({}_3^7Li\) đứng yên. Biết m_p = 1,0073u; m_Li = 7,0142u; m_X = 4,0015u; 1u = 931,5 MeV/c². Sau phản ứng xuất hiện hai hạt X giống nhau có cùng động năng và có phương chuyển động hợp với phương chuyển động của prôtôn một góc φ như nhau. Coi phản ứng không kèm theo bức xạ γ . Giá trị của φ là

Phương trình phản ứng hạt nhân: \(p + {}_3^7Li \to {}_2^4X + {}_2^4X\)

Năng lượng toả ra của phản ứng: \(\Delta E = \left( {{m_p} + {m_{Li}} - 2{m_X}} \right){c^2} = 2{K_X} - {K_p} \Rightarrow {K_X} = 9,866MeV\)

Định luật bảo toàn động lượng: \(\overrightarrow {{P_p}}  = \overrightarrow {{P_X}}  + \overrightarrow {{P_X}} \)

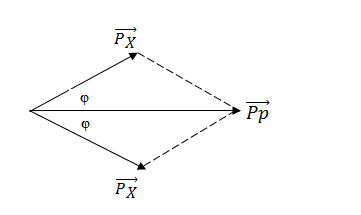
Áp dụng định lí hàm số cos trong tam giác ta được: \(P_X^2 = P_X^2 + P_p^2 - 2{P_X}{P_p}c{\rm{os}}\varphi \)

\( \Rightarrow \cos \varphi  = \frac{{p_p^2}}{{2{p_X}{p_p}}} = \frac{{{p_p}}}{{2{p_X}}} \Rightarrow {P_p} = 2{p_X}\cos \varphi \)  

\(\begin{array}{l} \Rightarrow p_p^2 = 4p_X^2{\cos ^2}\varphi  \Leftrightarrow {m_P}{K_P} = 4{m_X}{K_X}{\cos ^2}\varphi  \Rightarrow {\cos ^2}\varphi  = \dfrac{{{m_P}{K_P}}}{{4{m_X}{K_X}}} = \dfrac{{1.2,5}}{{4.4.9,866}}\\ \Rightarrow \varphi  = 82,{7^o}\end{array}\)