Bắn hạt proton có động năng 4,5 MeV vào hạt nhân \(_3^7Li\) đang đứng yên, gây ra phản ứng hạt nhân \(p + {}_3^7Li \to 2\alpha  + 17,3MeV\). Giả sử phản ứng không kèm theo bức xạ γ , hai hạt α có cùng động năng và bay theo hai hướng tạo với nhau góc β . Coi khối lượng của mỗi hạt tính theo đơn vị u gần đúng bằng số khối của nó. Giá trị của β là:

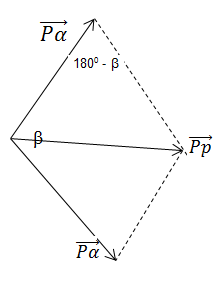
Bảo toàn động lượng: \(\overrightarrow {{P_p}}  = \overrightarrow {{P_\alpha }}  + \overrightarrow {{P_\alpha }} \)

Năng lượng toả ra của phản ứng: \(\Delta E = 2{K_\alpha } - {K_p} \Leftrightarrow 17,3 = 2{K_\alpha } - 4,5 \Rightarrow {K_\alpha } = 10,9MeV\)

Áp dụng định lí hàm số cos trong tam giác:

\(\begin{array}{l}P_p^2 = P_\alpha ^2 + P_\alpha ^2 - 2{P_\alpha }{P_\alpha }c{\rm{os}}\left( {180 - \beta } \right) \Rightarrow P_p^2 = 2P_\alpha ^2\left( {1 - c{\rm{os}}\left( {180 - \beta } \right)} \right)\\ \Rightarrow {m_p}{K_p} = 2{m_\alpha }{K_\alpha }\left( {1 - c{\rm{os}}\left( {180 - \beta } \right)} \right) \Rightarrow c{\rm{os}}\left( {180 - \beta } \right) = 1 - \dfrac{{{m_p}{K_p}}}{{2{m_\alpha }{K_\alpha }}} = 1 - \dfrac{{1.4,5}}{{2.4.10,9}} = \dfrac{{827}}{{872}}\\ \Rightarrow 180 - \beta  = 18,{5^0} \Rightarrow \beta  = 161,{5^0}\end{array}\)