Một vật dao động điều hoà có đồ thị như hình vẽ.
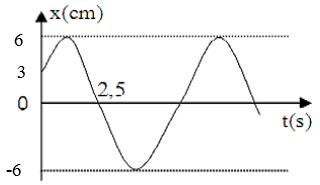
Phương trình dao động của vật là:
Từ đồ thị ta có:
+ Biên độ dao động : $A{\rm{ }} = {\rm{ }}4cm$
+ Thời gian khi vật đi từ vị trí \(\dfrac{A}{2}\) theo chiều dương đến vị trí cân bằng lần đầu tiên là:
\(\begin{array}{l}\Delta t = \dfrac{T}{6} + \dfrac{T}{4} = \dfrac{{5T}}{{12}} = 2,5s\\ \to T = 6s\\ \to \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{6} = \dfrac{\pi }{3}rad/s\end{array}\)
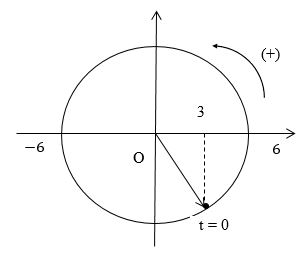
+ Ban đầu vật ở vị trí \(x = 3cm\) theo chiều dương
\(\left\{ \begin{array}{l}{x_0} = Acos\varphi = 3cm\\v = - A\omega \sin \varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}cos\varphi = \dfrac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{3}\)
=> Pha ban đầu của vật là \(\varphi = - \dfrac{\pi }{3}rad\)
=>Phương trình dao động của vật là: $x{\rm{ }} = 6cos(\dfrac{\pi }{3}t - \dfrac{\pi }{3})cm$
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 10 N/m và vật nhỏ có khối lượng 100 g dao động điều hòa trên quỹ đạo dài 8 cm. Tại thời điểm t = 0, vật đi qua vị trí có li độ -2 cm theo chiều dương. Phương trình dao động của vật là
Tần số góc của con lắc là:
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{10}}{{0,1}}} = 10\,\,\left( {rad/s} \right)\)
Chiều dài quỹ đạo dao động của con lắc là:
\(L = 2A \Rightarrow A = \frac{L}{2} = \frac{8}{2} = 4\,\,\left( {cm} \right)\)
Li độ và vận tốc của vật ở thời điểm t = 0 là:
\(\left\{ \begin{array}{l}x = 4\cos \varphi = - 2\\v = - 40\sin \varphi > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cos \varphi = - \frac{1}{2}\\\sin \varphi < 0\end{array} \right. \Rightarrow \varphi = - \frac{{2\pi }}{3}\,\,\left( {rad} \right)\)
Phương trình dao động của vật là: \(x = 4\cos \left( {10t - \frac{{2\pi }}{3}} \right)\,\,\left( {cm} \right)\)
Một vật nhỏ dao động theo phương trình \(x = Acos\left( {\omega t + \varphi } \right)\). Tại thời điểm ban đầu, vật đi qua vị trí có li độ \(x > 0\), hướng ra xa vị trí cân bằng. Giá trị của \(\varphi \) thỏa mãn:
Tại \(t = 0\) , ta có \(x > 0\) và hướng ra xa vị trí cân bằng => \(v > 0\)
\( \leftrightarrow \left\{ \begin{array}{l}{x_{t = 0}} = Ac{\rm{os}}\varphi {\rm{ > 0}}\\v = - A\omega \sin \varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}cos\varphi > 0\\\sin \varphi < 0\end{array} \right. \to - \dfrac{\pi }{2} < \varphi < 0\)
Một vật dao động điều hòa có đồ thị li độ theo thời gian như hình vẽ:
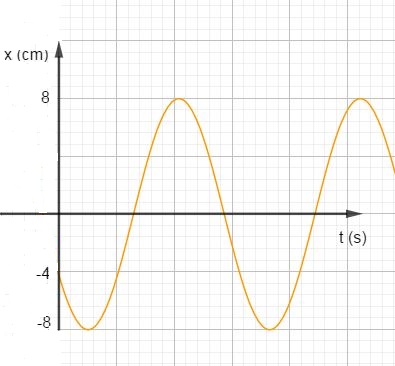
Pha ban đầu của dao động bằng:
Từ đồ thị ta có, biên độ: \(A = 8cm\)
Ta có: tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi {\rm{ = - 4cm}}\\v = - A\omega \sin \varphi < 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = - \dfrac{4}{8} = - \dfrac{1}{2}\\\sin \varphi > 0\end{array} \right. \to \varphi = \dfrac{{2\pi }}{3}\)
Một chất điểm dao động điều hòa với biên độ \(8cm\). Tại thời điểm ban đầu vật đang ở vị trí cân bằng và chuyển động theo chiều dương với độ lớn vận tốc \(16\pi cm/{s}\). Phương trình dao động điều hòa của vật là:
Ta có:
+ Biên độ dao động: \(A = 8cm\)
+ Khi vật qua VTCB, vận tốc của vật cực đại: \({v_{max}} = \omega A \to \omega = \dfrac{{{v_{max}}}}{A} = \dfrac{{16\pi }}{8} = 2\pi \left( {rad/s} \right)\)
+ Mặt khác, tại thời điểm ban đầu, vật đang ở VTCB và chuyển động theo chiều dương
\(t = 0:\left\{ \begin{array}{l}x = Acos\varphi = 0\\v = - A\omega \sin \varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}cos\varphi = 0\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{2}\)
=> Phương trình dao động của vật: \(x = 8cos\left( {2\pi t - \dfrac{\pi }{2}} \right)cm\)
Một vật dao động điều hòa có đồ thị li độ dao động theo thời gian như hình vẽ:
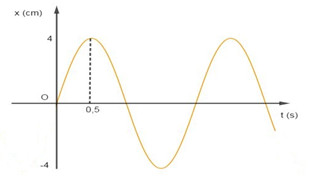
Phương trình dao động của vật là:
+ Từ đồ thị dao động, ta có:
Biên độ dao động: \(A = 4cm\)
+ Thời gian vật đi từ VTCB đến biên dương: \(\Delta t = \dfrac{T}{4} = 0,5s\)
\( \to T = 0,5.4 = 2s\)
\( \to \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{2} = \pi \left( {rad/s} \right)\)
+ Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 0\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = 0\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{2}\)
\( \to x = 4c{\rm{os}}\left( {\pi t - \dfrac{\pi }{2}} \right)cm\)
Một vật dao động điều hòa với biên độ \(4cm\). Tại thời điểm ban đầu, vật đang ở vị trí li độ \(x = 2cm\) chuyển động theo chiều dương đến biên dương và đến vị trí cân bằng lần thứ nhất hết \(2,5s\). Phương trình dao động của vật là:
Ta có:
+ Biên độ: \(A{\rm{ }} = {\rm{ }}4cm\)
+ Góc quét được khi vật đi từ vị trí \(2cm\) => biên dương => VTCB là:
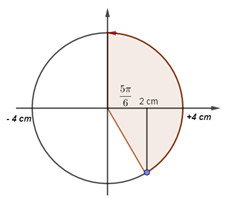
\(\begin{array}{l}\Delta \varphi = \omega \Delta t = \dfrac{{5\pi }}{6}\\ \to \omega .2,5 = \dfrac{{5\pi }}{6} \to \omega = \dfrac{\pi }{3}\left( {rad/s} \right)\end{array}\)
+ Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 2\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = \dfrac{2}{4} = \dfrac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{3}\)
\( \Rightarrow x = 4c{\rm{os}}\left( {\dfrac{\pi }{3}t - \dfrac{\pi }{3}} \right)cm\)
Một vật dao động điều hòa với biên độ \(4cm\) và chu kì \(2s\), chọn gốc thời gian là lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là
Ta có:
+ Tần số góc của dao động: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{2} = \pi \left( {rad/s} \right)\)
+ Biên độ dao động: \(A = 4cm\)
+ Tại \(t = 0\): \(\left\{ \begin{array}{l}{x_0} = 0\\v > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}cos\varphi = 0\\\sin \varphi < 0\end{array} \right. \Rightarrow \varphi = - \dfrac{\pi }{2}\)
Phương trình dao động của vật: \(x = 4cos\left( {\pi t - \dfrac{\pi }{2}} \right)cm\)
Một vật dao động điều hòa với phương trình \(x = 10\cos \left( {4\pi t + \dfrac{\pi }{2}} \right)\left( {cm} \right)\). Gốc thời gian được chọn vào lúc vật:
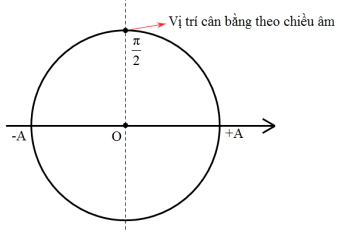
Từ phương trình: \(x = 10\cos \left( {4\pi t + \dfrac{\pi }{2}} \right)\left( {cm} \right)\)\( \Rightarrow \varphi = \dfrac{\pi }{2}rad\)
Biểu diễn trên VTLG ta có:
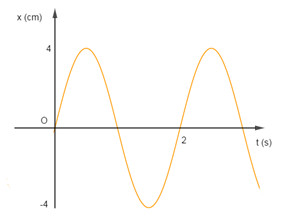
Một vật dao động điều hòa có đồ thị x-t như hình vẽ:
Phương trình dao động của vật là:
Từ đồ thị, ta có:
+ Biên độ dao động: \(A = 4cm\)
+ Chu kì dao động: \(T = 2s\)
=> Tần số góc: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{2} = \pi ra{\rm{d}}/s\)
+ Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 0\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = 0\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{2}\)
=> \(x{\rm{ }} = {\rm{ }}4cos\left( {\pi t - \dfrac{\pi }{2}} \right)\)
Một vật dao động điều hòa có chu dao động \(T = 2s\), vận tốc cực đại mà vật đạt được có giá trị \({v_{max}} = 6\pi \left( {cm/s} \right)\). Biết tại thời điểm ban đầu, vận tốc của vật bằng 0 và đang đi theo chiều âm. Phương trình dao động của vật là:
Ta có:
+ \(T{\rm{ }} = {\rm{ }}2s \to \omega = \dfrac{{2\pi }}{T} = \pi ra{\rm{d}}/s\)
+ Vận tốc cực đại: \({v_{max}} = A\omega = 6\pi cm/s \to A = \dfrac{{6\pi }}{\omega } = \dfrac{{6\pi }}{\pi } = 6cm\)
Tại t = 0: \({\rm{v = - A}}\omega {\rm{sin}}\varphi = 0 \to \sin \varphi = 0 \to \left( \begin{array}{l}\varphi = 0\\\varphi = \pi \end{array} \right.\)
Lại có, vật đang đi theo chiều âm\( \to \varphi = 0\)
\( \Rightarrow x = 6c{\rm{os}}\left( {\pi t} \right)cm\)
Phương trình nào dưới đây không biểu thị cho dao động điều hòa?
A, B, C – là phương trình của dao động điều hòa
D – không là phương trình dao động điều hòa vì: dao động điều hòa là dao động trong đó li độ của vật biến đổi theo hàm sin (hay cosin)
Phương trình nào sau đây biểu thị cho dao động điều hòa?
A, C, D – không biểu thị cho dao động điều hòa
B – biểu thị cho dao động điều hòa vì:
\(\begin{array}{l}x = 2\cos \left( {2\pi t + \dfrac{\pi }{2}} \right) + 2\sin \left( {2\pi t + \dfrac{\pi }{2}} \right)\\ = 2\left( {cos\left( {2\pi t + \dfrac{\pi }{2}} \right) + \sin \left( {2\pi t + \dfrac{\pi }{2}} \right)} \right)\\ = 2\left( {\sqrt 2 \sin \left( {2\pi t + \dfrac{\pi }{2} + \dfrac{\pi }{4}} \right)} \right)cm\end{array}\)
Trong các phương trình sau phương trình nào không biểu thị cho dao động điều hòa ?
B - không biểu thị cho dao động điều hòa vì biên độ dao động là hằng số chứ không phải là hàm của thời gian
Một vật dao động điều hòa với tần số $5 Hz$ và biên độ $8 cm$. Chọn gốc thời gian lúc vật qua vị trí cân bằng theo chiều âm. Phương trình dao động của là:
Ta có:
+ Biên độ dao động: \(A{\rm{ }} = {\rm{ }}8cm\)
+ Tần số góc: \(\omega = 2\pi f = 2\pi .5 = 10\pi rad/s\)
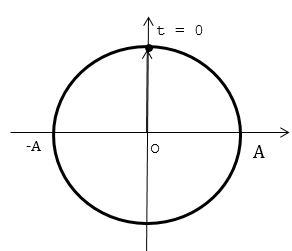
+ Gốc thời gian là lúc vật qua VTCB theo chiều âm:\(\varphi = \dfrac{\pi }{2}(rad)\)
$ \to x = 8cos\left( {10\pi t + \dfrac{\pi }{2}} \right)cm$
Một vật dao động điều hoà có phương trình $x = 4cos\left( {20\pi t - \dfrac{\pi }{6}} \right)cm$. Tần số và pha ban đầu của dao động lần lượt là:
Từ phương trình dao động: \(x = 4cos\left( {20\pi t - \dfrac{\pi }{6}} \right)cm\), ta có:
+ Tần số góc: \(\omega = 20\pi \left( {rad/s} \right) \to f = \dfrac{\omega }{{2\pi }} = \dfrac{{20\pi }}{{2\pi }} = 10Hz\)
+ Pha ban đầu của dao động: \(\varphi = - \dfrac{\pi }{6}\left( {rad} \right)\)
Gốc thời gian được chọn vào lúc nào nếu phương trình dao động điều hòa có dạng \(x = A\cos \left( {\omega t + {\pi \over 2}} \right)cm\)?
Phương trình dao động là: \(x = A\cos \left( {\omega t + {\pi \over 2}} \right)cm\)
Pha ban đầu là $π/2$.
Biểu diễn trên đường tròn lượng giác ta có:
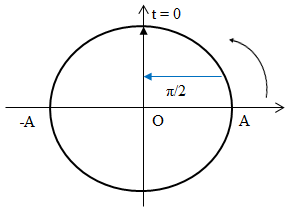 => Gốc thời gian được chọn là lúc chất điểm đi qua VTCB theo chiều âm quy ước.
=> Gốc thời gian được chọn là lúc chất điểm đi qua VTCB theo chiều âm quy ước.
Một vật dao động điều hòa với chu kỳ \(2\,\,s\). Chọn gốc tọa độ ở vị trí cân bằng, gốc thời gian là lúc vật có ly độ \(-2\sqrt{2}\,\,cm\) và đang chuyển động ra xa vị trí cân bằng với tốc độ \(2\pi \sqrt{2}\,\,cm/s\). Phương trình dao động của vật là
Tần số góc của dao động là:
\(\omega =\dfrac{2\pi }{T}=\dfrac{2\pi }{2}=\pi \,\,\left( rad/s \right)\)
Áp dụng công thức độc lập với thời gian, ta có:
\({{x}^{2}}+\dfrac{{{v}^{2}}}{{{\omega }^{2}}}={{A}^{2}}\Rightarrow {{\left( -2\sqrt{2} \right)}^{2}}+\frac{{{\left( 2\pi \sqrt{2} \right)}^{2}}}{{{\pi }^{2}}}={{A}^{2}}\Rightarrow A=4\,\,\left( cm \right)\)
Ở thời điểm đầu vật có li độ \(-2\sqrt{2}\,\,cm\) và đang chuyển động ra xa vị trí cân bằng, ta có vòng tròn lượng giác:
Từ vòng tròn lượng giác ta thấy pha ban đầu của dao động là: \(\dfrac{3\pi }{4}\,\,\left( rad \right)\)
Phương trình dao động của vật là: \(x=4\cos \left( \pi t+\dfrac{3\pi }{4} \right)\,\,\left( cm \right)\)
Một chất điểm dao động điều hòa dọc theo trục $Ox$, xung quanh VTCB $O$ với biên độ $4 cm$ và tần số $10 Hz$. Tại thời điểm ban đầu chất điểm có li độ $4 cm$. Phương trình dao động của chất điểm là:
Ta có:
+ Biên độ dao động: \(A{\rm{ }} = {\rm{ }}4cm\)
+ Tần số góc: \(\omega = 2\pi f = 2\pi .10 = 20\pi \left( {rad/s} \right)\)
+ Lúc \(t = 0\) vật ở biên dương, ta suy ra: \(\varphi = 0\left( {rad} \right)\)
=> Phương trình dao động của vật: \(x = 4cos\left( {20\pi t} \right)cm\)
Một vật dao động điều hòa với chu kì $T{\rm{ }} = {\rm{ }}1s$. Tại thời điểm $t{\rm{ }} = {\rm{ }}0$, vật đi qua vị trí có li độ \(x = - 5\sqrt 2 cm\) với vận tốc \(v = - 10\pi \sqrt 2 cm/s\). Phương trình dao động của vật là:
\(T = 1s \Rightarrow \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{1} = 2\pi (rad)\)
Ta sử dụng phương trình độc lập theo thời gian của x và v để tìm biên độ dao động
\(A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{{\left( { - 5\sqrt 2 } \right)}^2} + \dfrac{{{{\left( { - 10\pi \sqrt 2 } \right)}^2}}}{{{{\left( {2\pi } \right)}^2}}}} = 10cm\)
Tai thời điểm ban đầu vật ở vị trí \(x = - 5\sqrt 2cm \) và có vận tốc âm nên khi biểu diễn trên đường tròn ta được pha ban đầu: \(\varphi = \dfrac{{3\pi }}{4}rad\)
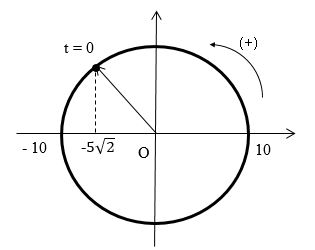
Khi đó ta có phương trình dao động là: \(x = A\cos (\omega t + \varphi ) = 10\cos (2\pi t + \dfrac{{3\pi }}{4})cm\)

