Một vật dao động điều hòa với biên độ $A{\rm{ }} = {\rm{ }}8cm$ và \(\omega = \pi \left( {rad/s} \right)\). Tại thời điểm ban đầu vật qua vị trí có li độ ${x_0} = {\rm{ }}4cm$ theo chiều dương. Phương trình dao động của vật là:
Ta có:
+ Biên độ dao động:$A{\rm{ }} = 8cm$
+ Tần số góc của dao động: \(\omega = \pi \left( {rad/s} \right)\)
+ Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 4\\v = - {\rm{A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}cos\varphi = \dfrac{{{x_0}}}{A} = \dfrac{4}{8} = \dfrac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{3}\)
$ = > x = 8cos(\pi t - \dfrac{\pi }{3})\left( {cm} \right)$
Một vật nhỏ dao động điều hòa dọc theo trục Ox với biên độ $5cm$, chu kỳ $2s$. Tại thời điểm $t = 0$, vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là
Ta có:
$\begin{gathered}A = 5cm \hfill \\T = 2{\text{s}} \to \omega = \frac{{2\pi }}{T} = \pi ra{\text{d}}/s \hfill \\\end{gathered} $
Tại t=0 $\left\{ \begin{gathered}x = 0 \hfill \\ v > 0 \hfill \\\end{gathered} \right. \leftrightarrow \left\{ \begin{gathered}{\text{cos}}\varphi = 0 \hfill \\\sin \varphi < 0 \hfill \\\end{gathered} \right. \to \varphi = - \frac{\pi }{2}$
$ \to x = Ac{\text{os(}}\omega {\text{t + }}\varphi {\text{) = 5cos(}}\pi {\text{t - }}\frac{\pi }{2})cm$
Một chất điểm chuyển động tròn đều trong mặt phẳng thẳng đứng, có bán kính quỹ đạo là $8cm$, bắt đầu từ vị trí thấp nhất của đường tròn theo chiều ngược chiều kim đồng hồ với tốc độ không đổi là $16π cm/s$. Hình chiếu của chất điểm lên trục Ox nằm ngang, đi qua tâm O của đường tròn, nằm trong mặt phẳng quỹ đạo có chiều từ trái qua phải là
Ta có:
\(\begin{array}{l}A = 8cm\\v = \omega R = \omega A = 16\pi \to \omega = \dfrac{{16\pi }}{8} = 2\pi \end{array}\)
Mặt khác, tại thời điểm ban đầu, chất điểm đi qua tâm \(O{\rm{ }} = > {\rm{ }}x = 0\), nằm trong mặt phẳng có quỹ đạo có chiều từ trái qua phải $=> v > 0$
\(\begin{array}{l} \to \varphi = - \dfrac{\pi }{2}\\ \to x = 8c{\rm{os(2}}\pi {\rm{t - }}\dfrac{\pi }{2})cm\end{array}\)
Một chất điểm dao động điều hoà với phương trình dạng \(x = cos\left( {2\pi t + \frac{\pi }{6}} \right)\left( {cm,{\text{ }}s} \right)\). Lấy ${\pi ^2} = 10$, biểu thức gia tốc tức thời của chất điểm là:
Ta có: $a = - {\omega ^2}Acos(\omega t + \varphi ) = {\omega ^2}Acos(\omega t + \varphi + \pi )$
x = cos(2πt + π/6) (cm, s) $ \to a = - {(2\pi )^2}.1cos(2\pi t + \frac{\pi }{6}) = - 40cos(2\pi t + \frac{\pi }{6})$
Phương trình dao động điều hòa có dạng \(x = Acos\omega t\). Gốc thời gian được chọn là:
Từ phương trình dao động, ta có:
Gốc thời gian $t = 0$:
$x = Ac{\text{os0 = A}}$
Phương trình dao động của một vật có dạng $x = A\sin (\omega t + \frac{\pi }{4})$.Chọn kết luận đúng?
Ta có: $x = A\sin \left( {\omega t + \dfrac{\pi }{4}} \right) = Ac{\text{os}}\left( {\omega t + \dfrac{\pi }{4} - \dfrac{\pi }{2}} \right) = Ac{\text{os}}\left( {\omega t - \dfrac{\pi }{4}} \right)$
- Biên độ dao động của vật là $A$
- Pha ban đầu: \(\varphi = - \dfrac{\pi }{4}\)
Một vật nhỏ dao động theo phương trình $x = Acos(ωt + φ) (cm)$. Tại thời điểm ban đầu, vật đi qua vị trí có li độ $x < 0$, hướng ra xa vị trí cân bằng. Giá trị của $φ$ thỏa mãn:
Tại $t = 0$, ta có $x < 0$ và hướng ra xa vị trí cân bằng $=> v < 0$
$ \leftrightarrow \left\{ \begin{array}{l}
Ac{\rm{os}}\varphi {\rm{ < 0}}\\
v = - A\omega \sin \varphi < 0
\end{array} \right. \to \left\{ \begin{array}{l}
c{\rm{os}}\varphi {\rm{ < 0}}\\
\sin \varphi > 0
\end{array} \right. \to \frac{\pi }{2} < \varphi < \pi $
Một vật dao động điều hòa với biên độ $A = 8 cm$. Tại thời điểm $t = 0$, vật có li độ $x = -4 cm$ và đang đi theo chiều âm của trục $Ox$. Pha ban đầu của dao động bằng:
Ta có: tại t = 0:
\(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi {\rm{ = - 4}}\\v = - A\omega \sin \varphi < 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = - \dfrac{4}{8} = - \dfrac{1}{2}\\\sin \varphi > 0\end{array} \right. \to \varphi = \dfrac{{2\pi }}{3}\)
Cho một chất điểm dao động điều hòa với tần số $1Hz$, thời điểm đầu vật qua vị trí $x = 5cm$ theo chiều dương với tốc độ \(v = 10\pi cm/s\). Viết phương trình dao động.
Ta có:
Tốc độ góc: $\omega = 2\pi f = 2\pi .1 = 2\pi (ra{\rm{d}}/s)$
Biên độ dao động:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {5^2} + {\left( {\frac{{10\pi }}{{2\pi }}} \right)^2} \to A = 5\sqrt 2 cm\)
Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 5\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{5}{{5\sqrt 2 }}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{4}\)
=> \(x = 5\sqrt 2 {\rm{cos}}\left( {2\pi t - \frac{\pi }{4}} \right)cm = 5\sqrt 2 \sin \left( {2\pi t - \frac{\pi }{4} + \frac{\pi }{2}} \right) = 5\sqrt 2 \sin \left( {2\pi t + \frac{\pi }{4}} \right)cm\)
Một vật dao động điều hoà dọc theo trục $Ox$ nằm ngang, gốc $O$ và mốc thế năng ở vị trí cân bằng. Thời gian vật đi từ VTCB đến $A$ hết $0,5s$ và đi hết quãng đường $4cm$ Chọn \(t=0\) lúc vật qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là:
Ta có: Thời gian vật đi từ VTCB đến $A$ là :
\(\frac{T}{4} = 0,5 \to T = 2{\rm{s}} \to \omega = \frac{{2\pi }}{T} = \pi ra{\rm{d}}/s\)
Biên độ A = 4cm
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 0\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = 0\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{2}\)
\( \to x = 4c{\rm{os}}\left( {\pi t - \frac{\pi }{2}} \right)cm\)
Một vật dao động điều hoà có đồ thị như hình vẽ.
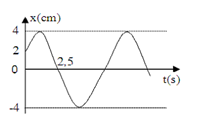
Phương trình dao động của vật là:
Từ đồ thị, ta có: \(A{\text{ }} = {\text{ }}4cm\)
Thời gian vật đi từ \(t = 0{\text{ }}\left( {x = \frac{A}{2}} \right)\) đến \(t = 2,5s{\text{ }}\left( {x = 0} \right)\) là:
\(\Delta t = 2,5{\rm{s}} = \frac{T}{6} + \frac{T}{4} = \frac{{5T}}{{12}} \to T = 6{\rm{s}} \to \omega = \frac{{2\pi }}{T} = \frac{\pi }{3}ra{\rm{d}}/s\)
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 2\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = \frac{2}{4} = \frac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{3}\)
\( \Rightarrow x = 4c{\rm{os}}\left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)cm\)
Vật nặng dao động điều hòa với \(\omega = 10\sqrt 5 rad/s\). Chọn gốc tọa độ trùng với vị trí cân bằng của vật. Biết rằng tại thời điểm ban đầu vật đi qua li độ $x = 2cm$ với vận tốc \(v = 20\sqrt {15} cm/s\). Phương trình dao động của vật là:
Ta có: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {2^2} + \frac{{{{\left( {20\sqrt {15} } \right)}^2}}}{{{{\left( {10\sqrt 5 } \right)}^2}}} = 16 \to A = 4cm\)
Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 2\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{2}{4} = \frac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{3}\)
\( \Rightarrow x = 4c{\rm{os}}\left( {10\sqrt 5 t - \frac{\pi }{3}} \right)cm\)
Một vật dao động điều hòa với biên độ $A = 8cm$ và $ω = π rad/s$. Tại thời điểm ban đầu vật qua vị trí có li độ \({x_0} = {\text{ }}4cm\) theo chiều âm. Phương trình dao động của vật là:
Ta có A =8cm, ω = π rad/s
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 4\\{\rm{v = - A}}\omega {\rm{sin}}\varphi < 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{{{x_0}}}{A} = \frac{4}{8} = \frac{1}{2}\\\sin \varphi > 0\end{array} \right. \to \varphi = \frac{\pi }{3}\)
=> x =8cos(πt +π/3)(cm)
Một vật dao động điều hòa trên quỹ đạo dài $8cm$ với chu kì $T=2s$. Chọn gốc thời gian là lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là :
Ta có: $L=2A = 8cm => A = 4cm$
Tần số góc: $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{2} = \pi ra{\rm{d}}/s$
Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 0\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = 0\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{2}\)
=> $x{\rm{ }} = {\rm{ }}4cos\left( {\pi t - \frac{\pi }{2}} \right)$
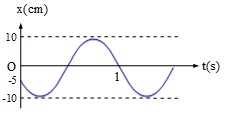
Một chất điểm dao động điều hòa có đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ như hình vẽ. Phương trình dao động của vật là:
Từ đồ thị, ta có: A = 10cm
Thời gian vật đi từ t = 0 (x= -A/2) đến t = 1s (x = 0) tương đương các vị trí (-A/2 => -A =>A => 0) là:
\(\Delta t = 1{\rm{s}} = \frac{T}{6} + \frac{{3T}}{4} = \frac{{11T}}{{12}} \to T = \frac{{12}}{{11}}{\rm{s}} \to \omega = \frac{{2\pi }}{T} = \frac{{11\pi }}{6}ra{\rm{d}}/s\)
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = - 5\\{\rm{v = - A}}\omega {\rm{sin}}\varphi < 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = \frac{{ - 2}}{{10}} = \frac{{ - 1}}{2}\\\sin \varphi > 0\end{array} \right. \to \varphi = \frac{{2\pi }}{3}\)
\( \Rightarrow x{\rm{ }} = {\rm{ }}10cos\left( {\frac{{11\pi }}{6}t + \frac{{2\pi }}{3}} \right)cm\)
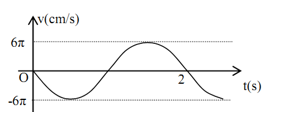
Đồ thị vận tốc của một vật cho ở hình bên, phương trình nào dưới đây là phương trình dao động của vật:
Từ đồ thị, ta có: $T{\rm{ }} = {\rm{ }}2s \to \omega = \frac{{2\pi }}{T} = \pi ra{\rm{d}}/s$
$A\omega = 6\pi cm/s \to A = \frac{{6\pi }}{\omega } = \frac{{6\pi }}{\pi } = 6cm$
Tại t = 0: \({\rm{v = - A}}\omega {\rm{sin}}\varphi = 0 \to \sin \varphi = 0 \to \left[ \begin{array}{l}\varphi = 0\\\varphi = \pi \end{array} \right.\)
và đang đi theo chiều âm\( \to \varphi = 0\)
\( \Rightarrow x = 6c{\rm{os}}\left( {\pi t} \right)cm\)
Chọn phương trình biểu thị cho dao động điều hòa:
A - loại do biên độ A không phải là hàm theo thời gian
B và D - loại vì pha ban đầu φ không phải là hàm theo thời gian
Trong các phương trình sau phương trình nào không biểu thị cho dao động điều hòa ?
B- không biểu thị cho dao động điều hòa vì biên độ dao động không phải là hàm của thời gian
Trong các phương trình sau phương trình nào không biểu thị cho dao động điều hòa ?
B- không biểu thị cho dao động điều hòa vì biên độ dao động không phải là hàm của thời gian

