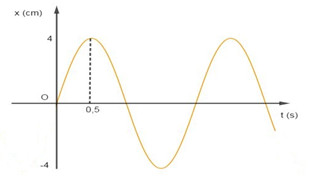
Một vật dao động điều hoà dọc theo trục $Ox$ nằm ngang, gốc $O$ và mốc thế năng ở vị trí cân bằng. Thời gian vật đi từ VTCB đến $A$ hết $0,5s$ và đi hết quãng đường $4cm$ Chọn \(t=0\) lúc vật qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là:

\(x = 6cos\left( {\dfrac{\pi }{3}t - \dfrac{\pi }{3}} \right)cm\)

\(x = 6cos\left( {\dfrac{\pi }{3}t + \dfrac{\pi }{6}} \right)cm\)

\(x = 6cos\left( {\pi t - \dfrac{\pi }{6}} \right)cm\)

\(x = 6cos\left( {\dfrac{{2\pi }}{3}t - \dfrac{{5\pi }}{6}} \right)cm\)

\(\dfrac{\pi }{2} < \varphi < \pi \)

\( - \dfrac{\pi }{2} < \varphi < 0\)

\( - \pi < \varphi <  - \dfrac{\pi }{2}\)  

\(0 < \varphi < \dfrac{\pi }{2}\)

\( - \dfrac{\pi }{3}\)

\(\dfrac{\pi }{3}\)

\( - \dfrac{{2\pi }}{3}\)

\(\dfrac{{2\pi }}{3}\)

\({\rm{x}} = 16c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{2}} \right)(cm)\)

\({\rm{x}} = 16c{\rm{os}}\left( {2\pi t + \dfrac{\pi }{2}} \right)(cm)\)

\({\rm{x}} = 8c{\rm{os}}\left( {2\pi t + \dfrac{\pi }{2}} \right)(cm)\)

\({\rm{x}} = 8c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{2}} \right)(cm)\)

\(x = 2c{\rm{os}}\left( {\pi t - \dfrac{\pi }{2}} \right)cm\)

\(x = 4c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{2}} \right)cm\)

\(x = 2c{\rm{os}}\left( {\pi t + \dfrac{\pi }{2}} \right)cm\)

\(x = 4c{\rm{os}}\left( {\pi t - \dfrac{\pi }{2}} \right)cm\)

\(x = 4c{\rm{os}}\left( {\dfrac{\pi }{3}t - \dfrac{\pi }{3}} \right)cm\)

\(x = 4c{\rm{os}}\left( {\dfrac{\pi }{3}t + \dfrac{\pi }{6}} \right)cm\)

\(x = 4c{\rm{os}}\left( {\pi t - \dfrac{\pi }{6}} \right)cm\)

\(x = 4c{\rm{os}}\left( {\dfrac{{2\pi }}{3}t - \dfrac{{5\pi }}{6}} \right)cm\)