Câu hỏi:
2 năm trước
Một vật dao động điều hòa với biên độ \(4cm\). Tại thời điểm ban đầu, vật đang ở vị trí li độ \(x = 2cm\) chuyển động theo chiều dương đến biên dương và đến vị trí cân bằng lần thứ nhất hết \(2,5s\). Phương trình dao động của vật là:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có:
+ Biên độ: \(A{\rm{ }} = {\rm{ }}4cm\)
+ Góc quét được khi vật đi từ vị trí \(2cm\) => biên dương => VTCB là:
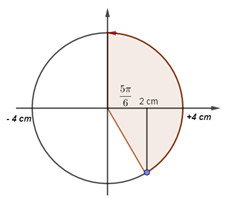
\(\begin{array}{l}\Delta \varphi = \omega \Delta t = \dfrac{{5\pi }}{6}\\ \to \omega .2,5 = \dfrac{{5\pi }}{6} \to \omega = \dfrac{\pi }{3}\left( {rad/s} \right)\end{array}\)
+ Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 2\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi = \dfrac{2}{4} = \dfrac{1}{2}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \dfrac{\pi }{3}\)
\( \Rightarrow x = 4c{\rm{os}}\left( {\dfrac{\pi }{3}t - \dfrac{\pi }{3}} \right)cm\)
Hướng dẫn giải:
- Xác định biên độ A
- Vận dụng vòng tròn lượng giác và biểu thức: \(\Delta \varphi = \omega \Delta t\)
- Xác định pha ban đầu: Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi \\{\rm{v = - A}}\omega {\rm{sin}}\varphi \end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\dfrac{{{x_0}}}{A}\\\sin \varphi = - \dfrac{v}{{A\omega }}\end{array} \right. \to \varphi = ?\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
