Một vật dao động điều hòa với phương trình là \(x = 4cos\left( {2\pi t} \right)cm\). Thời gian ngắn nhất để vật đi qua vị trí cân bằng kể từ thời điểm ban đầu là:
Ta thấy tại thời điểm ban đầu vật xuất phát từ vị trí biên dương ứng dụng vòng tròn lượng giác ta có:
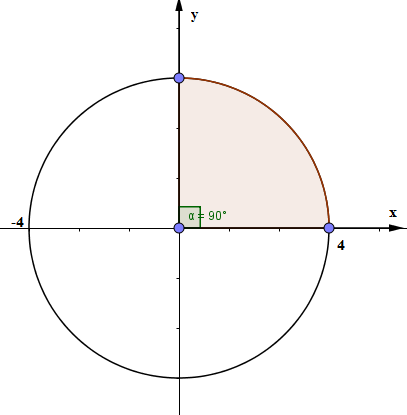
Từ đường tròn lượng giác ta thấy thời gian ngắn nhất khi vật đi từ vị trí biên dương đến vị trí cân bằng quét được 1 góc \(\dfrac{\pi }{2}\) vậy áp dụng mối liên hệ gữa góc quét \(\alpha \) và khoảng thời gian \(\Delta t\) thì ta có:
\(\alpha = \dfrac{\pi }{2} = > \Delta t = \dfrac{\alpha }{\omega } = \dfrac{{\dfrac{\pi }{2}.T}}{{2\pi }} = \dfrac{T}{4}\)
Mà \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1s = > \Delta t = \dfrac{1}{4}s\)
Vật dao động điều hòa theo phương trình \(x = Acos\left( {\pi t - \frac{\pi }{6}} \right)cm\). Thời điểm vật đi qua vị trí cân bằng là:
Khi ở vị trí cân bằng, vật có li độ: \(x = 0\)
\(\begin{array}{l}Acos\left( {\pi t - \frac{\pi }{6}} \right) = 0\\ \leftrightarrow cos\left( {\pi t - \frac{\pi }{6}} \right) = 0\\ \to \pi t - \frac{\pi }{6} = \frac{\pi }{2} + k\pi \\ \to t = \frac{2}{3} + k\end{array}\)
Một vật dao động điều hòa với T. Hãy xác định thời gian ngắn nhất để vật đi từ vị trí cân bằng đến \(\frac{{A\sqrt 2 }}{2}\)?
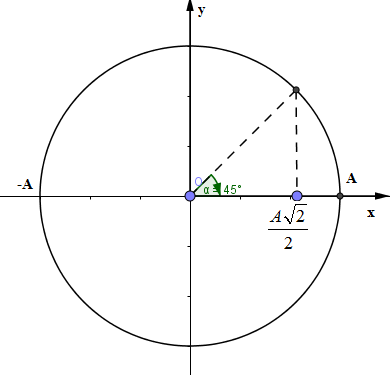
Từ đường tròn lượng giác ta thấy thời gian ngắn nhất vật đi từ vị trí cân bằng đến vị trí \(\frac{A}{2}\) thì quét được 1 góc \(\frac{\pi }{4}\)vậy áp dụng mối liên hệ gữa góc quét \(\alpha \) và khoảng thời gian \(\Delta t\) thì ta có:
\(\alpha = \frac{\pi }{4} = > \Delta t = \frac{\alpha }{\omega } = \frac{{\frac{\pi }{4}.T}}{{2\pi }} = \frac{T}{8}\)
Một vật dao động điều hòa với phương trình \(x = 5cos\left( {4\pi t - \frac{\pi }{2}} \right)cm\). Xác định thời gian ngắn nhất để vật đi từ vị trí \(2,5cm\) đến \( - 2,5cm\)?
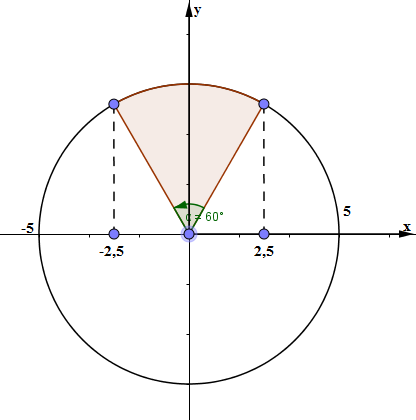
Từ đường tròn lượng giác ta thấy thời gian ngắn nhất khi vật đi từ vị trí 2,5 cm đến vị trí -2,5 cm quét được 1 góc \(\frac{\pi }{3}\) vậy áp dụng mối liên hệ gữa góc quét \(\alpha \) và khoảng thời gian \(\Delta t\) thì ta có:
\(\alpha = \frac{\pi }{3} = > \Delta t = \frac{\alpha }{\omega } = \frac{{\frac{\pi }{3}.T}}{{2\pi }} = \frac{T}{6}\)
Mà \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = \frac{1}{2}s = > \Delta t = \frac{{\frac{1}{2}}}{6} = \frac{1}{{12}}s\)
Một vật dao động điều hòa từ A đến B với chu kỳ T, vị trí cân bằng O. Trung điểm OA, OB là M, N. Thời gian ngắn nhất để vật đi từ M đến N là \(\frac{1}{{30}}\)s. Hãy xác định chu kỳ dao động của vật.
Ta có
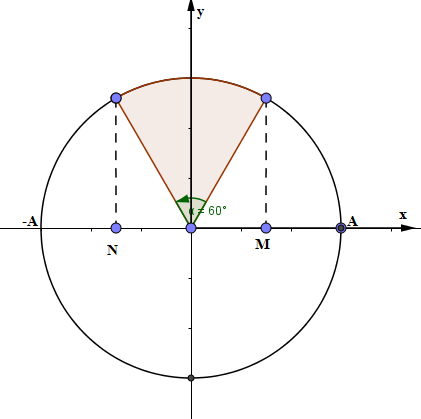
Từ đường tròn lượng giác ta thấy thời gian ngắn nhất khi vật đi từ vị trí M đến vị trí N quét được 1 góc \(\frac{\pi }{3}\) vậy áp dụng mối liên hệ gữa góc quét \(\alpha \) và khoảng thời gian \(\Delta t\) thì ta có:
\(\alpha = \frac{\pi }{3} = > \Delta t = \frac{\alpha }{\omega } = \frac{{\frac{\pi }{3}.T}}{{2\pi }} = \frac{T}{6} = \frac{1}{{30}} = > T = \frac{1}{5}s\)
Một vật dao động điều hoà với phương trình \(x = Acos\left( {\omega t + \dfrac{\pi }{3}} \right)cm\). Biết quãng đường vật đi được trong thời gian 1(s) là 2A và \(\dfrac{2}{3}\)s đầu tiên là $9cm$. Giá trị của $A$ và $\omega$ là:
+ Ta có : Vật đi được quãng đường \(2A\) trong khoảng thời gian \(\dfrac{T}{2}\)
\(\dfrac{T}{2} = 1s = > T = 2s = > \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{2} = \pi \,rad/s\)
Vậy ta có \(\dfrac{2}{3}s = \dfrac{T}{3} = > \alpha = \dfrac{{2\pi }}{3}\)
+ Tại thời điểm ban đầu \(t = 0\), ta có: \(\left\{ \begin{array}{l}{x_0} = Acos\left( {\dfrac{\pi }{3}} \right)\\{v_0} = - A\omega \sin \left( {\dfrac{\pi }{3}} \right)\end{array} \right. \to \left\{ \begin{array}{l}{x_0} = \dfrac{A}{2}\\{v_0} < 0\end{array} \right.\)
Ứng dụng vòng tròn lượng giác ta được:
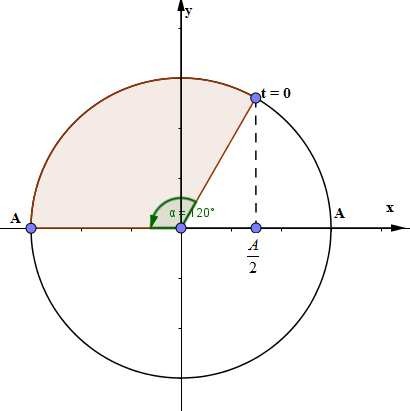
Từ đường tròn lượng giác ta thấy quãng đường vật đi trong \(\dfrac{2}{3}\)s đầu tiên là 9cm tương ứng với $1,5A$ trên đường tròn lượng giác do đó : $1,5 A = 9 => A = 6 cm$
Một vật dao động điều hoà với phương trình \(x = 5cos\left( {10\pi t} \right)cm\). Trong một chu kỳ thời gian vật có vận tốc nhỏ hơn \(25\pi cm/s\) là:
Ta có:
+ Vận tốc cực đại: \({v_{max}} = \omega A = 10\pi .5 = 50\pi \left( {cm/s} \right)\)
Theo đề, bài ta có: \(\left| v \right| = 25\pi \left( {cm/s} \right) = \dfrac{{{v_{max}}}}{2}\), vẽ trên vòng tròn lượng giác, ta được:
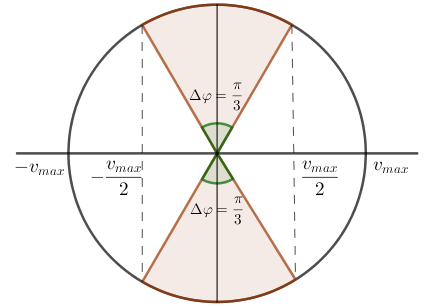
Từ đường tròn lượng giác ta thấy thời gian vật có vận tốc nhỏ hơn \(25\pi cm/s\) khi chuyển động quét được 1 góc \(\alpha = 2.\Delta \varphi = 2.\dfrac{\pi }{3} = \dfrac{{2\pi }}{3}\) vậy áp dụng mối liên hệ gữa góc quét \(\alpha \) và khoảng thời gian \(\Delta t\) thì ta có:
\(\alpha = \omega \Delta t\)
=> Trong một chu kỳ thời gian vật có vận tốc nhỏ hơn \(25\pi cm/s\) là:
\( \Rightarrow \Delta t = \dfrac{\alpha }{\omega } = \dfrac{{\dfrac{{2\pi }}{3}}}{{10\pi }} = \dfrac{1}{{15}}s\)
Vật dao động với phương trình \(x = 5cos\left( {4\pi t + \frac{\pi }{6}} \right)cm\). Tìm thời điểm vật đi qua vị trí biên dương lần thứ \(4\) kể từ thời điểm ban đầu.
Ta có:
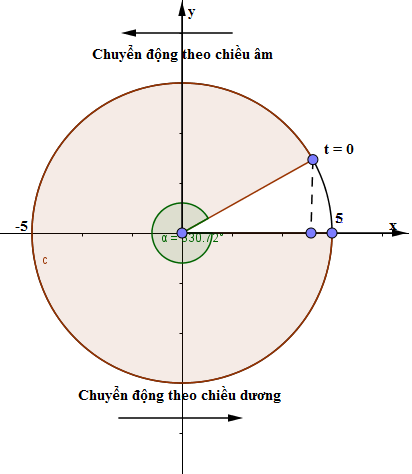
Thời điểm gian vật đi từ vị trí ban đầu đến vị trí biên dương lần thứ nhất vật quét được 1 góc \(\alpha = \frac{{11\pi }}{6}\), vậy áp dụng mối liên hệ gữa góc quét \(\alpha \) và khoảng thời gian \(\Delta t\) thì ta có:
\(\alpha = \frac{{11\pi }}{6} = > \Delta t = \frac{\alpha }{\omega } = \frac{{\frac{{11\pi }}{6}.T}}{{2\pi }} = \frac{{11T}}{{12}}\)
Mặt khác ta thấy từ đường tròn lượng giác trong 1 chu kỳ vật đi qua vị trí biên dương 1 lần do đó
Thời điểm vật đi qua vị trí vị trí biên dương lần thứ 4 kể từ thời điểm ban đầu là: \(t = \frac{{11T}}{{12}} + 3T\)
Với: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = \frac{1}{2} = > t = \frac{{11}}{{12}}.\frac{1}{2} + 3.\frac{1}{2} = 1,96s\)
Vật dao động với phương trình \(x = 5cos\left( {4\pi t + \frac{\pi }{6}} \right)cm\). Tìm thời điểm vật qua vị trí cân bằng lần thứ 4 kể từ thời điểm ban đầu.
Ta có
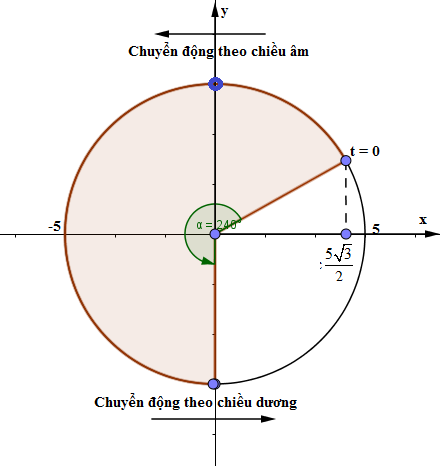
Thời điểm gian vật đi từ vị trí ban đầu đến vị trí cân bằng lần thứ hai vật quét được 1 góc \(\alpha = \frac{{4\pi }}{3}\), vậy áp dụng mối liên hệ gữa góc quét α và khoảng thời gian ∆t thì ta có
\(\alpha = \frac{{4\pi }}{3} = > \Delta t = \frac{\alpha }{\omega } = \frac{{\frac{{4\pi }}{3}.T}}{{2\pi }} = \frac{{2T}}{3}\)
Mặt khác ta thấy từ đường tròn lượng giác trong 1 chu kỳ vật đi qua vị trí cân bằng 2 lần do đó
Thời điểm vật đi qua vị trí vị trí cân bằng lần thứ 4 kể từ thời điểm ban đầu là: \(t = \Delta t + {t_2} = \frac{{2T}}{3} + T = \frac{{5T}}{3}\)
Với \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = \frac{1}{2} = > t = \frac{5}{3}.\frac{1}{2}s = \frac{5}{6}s\)
Một vật dao động được kích thích để dao động điều hòa với vận tốc cực đại bằng \(3m/s\) và gia tốc cực đại bằng \(30\pi m/{s^2}\). Thời điểm ban đầu \(t = 0\) vật có vận tốc \(v = + 1,5m/s\) và thế năng đang giảm. Hỏi sau đó bao lâu vật có gia tốc bằng \(- 15\pi \left( {m/{s^2}} \right)\)
+ Ta có: \(\left\{ \begin{array}{l}{v_{{\rm{max}}}} = \omega A\\{a_{{\rm{max}}}} = {\omega ^2}A\end{array} \right. \to \left\{ \begin{array}{l}\dfrac{{{a_{{\rm{max}}}}}}{{{v_{{\rm{max}}}}}} = \omega = \dfrac{{30\pi }}{3} = 10\pi \\A = \dfrac{{{v_{{\rm{max}}}}}}{\omega } = \dfrac{3}{{10\pi }}m\end{array} \right.\)
\( \to T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{10\pi }} = 0,2s\)
+ Tại \(t{\rm{ }} = {\rm{ }}0\): \(v{\rm{ }} = {\rm{ }} + 1,5m/s\) và thế năng đang giảm
Sử dụng hệ thức độc lập, ta có: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \to {x^2} = {A^2} - \dfrac{{{v^2}}}{{{\omega ^2}}} = {\left( {\dfrac{3}{{10\pi }}} \right)^2} - \dfrac{{{{1,5}^2}}}{{{{\left( {10\pi } \right)}^2}}} \to x = \pm \dfrac{{1,5\sqrt 3 }}{{10\pi }} = \pm \dfrac{{A\sqrt 3 }}{2}\)
Thế năng đang giảm => lấy \(x = - \dfrac{{A\sqrt 3 }}{2}\)
Khi vật có gia tốc \(a = - 15\pi \left( {m/{s^2}} \right) = - {\omega ^2}{x_2} \to {x_2} = - \dfrac{{ - 15\pi }}{{{{\left( {10\pi } \right)}^2}}} = \dfrac{{1,5}}{{10\pi }} = \dfrac{A}{2}\)
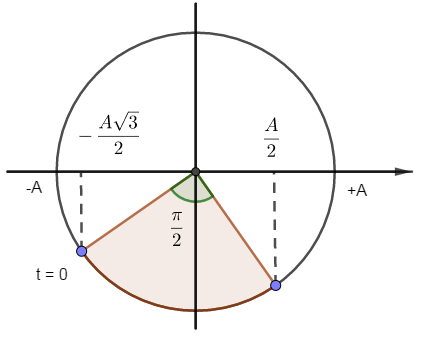
=> Thời gian để vật đi từ \(t = 0\) đến vị trí có \(a = - 15{\pi ^2}\left( {m/{s^2}} \right)\) là: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{\pi }{2}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{T}{4} = \dfrac{{0,2}}{4} = 0,05s\)
Một chất điểm dao động điều hòa theo phương trình \(x = 4c{\rm{os}}\left( {\dfrac{{2\pi }}{3}t} \right)cm\) (x tính bằng cm, t tính bằng giây). Kể từ \(t = 0\), chất điểm đi qua vị trí có li độ \(x = - 2cm\) lần thứ $2019$ tại thời điểm:
Ta có:
+ Chu kỳ: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{\dfrac{{2\pi }}{3}}} = 3s\)
+ \({t_{2019}} = {t_{2018}} + {t_1}\)
Ta có: Trong một chu kỳ, chất điểm đi qua vị trí có li độ \(x = - 2cm\) hai lần
=> \({t_{2018}} = \dfrac{{2018T}}{2} = 1009T\)
Tại \(t = 0\), vật ở li độ: \(x = 4cos0 = 4cm\)
=> \({t_1}\) là khoảng thời gian chất điểm đi từ \(x = A\) (vị trí ban đầu) đến \(x = - 2cm = - \dfrac{A}{2}\)
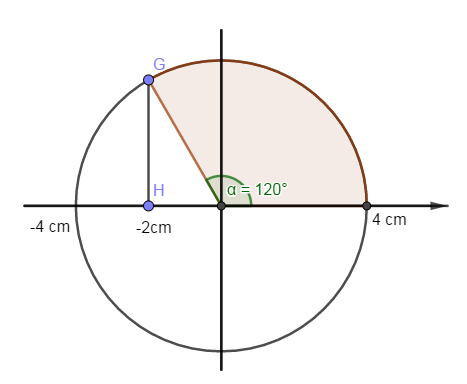
Góc quét: \(\Delta \varphi = {120^0} = \frac{{2\pi }}{3}\)
=> \({t_1} = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{{2\pi }}{3}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{T}{3}\)
\( \to {t_{2019}} = {t_{2018}} + {t_1} = 1009T + \dfrac{T}{3} = \dfrac{{3028T}}{3} = \dfrac{{3028.3}}{3} = 3028{\rm{s}}\)
Một vật dao động điều hòa với phương trình \(x = Acos\left( {\omega t} \right)cm\), chu kì dao động \(T\). Kể từ thời điểm ban đầu thì sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cân bằng lần thứ \(2012\)?
Ta có :
+ \({t_{2012}} = {t_{2010}} + {t_2}\)
Mặt khác, trong 1 chu kì vật đi qua VTCB 2 lần.
\( \to {t_{2010}} = \frac{{2010}}{2}T = 1005T\)
+ Tại t = 0 thì \(\left\{ \begin{array}{l}x = A\\v < 0\end{array} \right.\)
Xác định trên vòng tròn lượng giác, ta được:
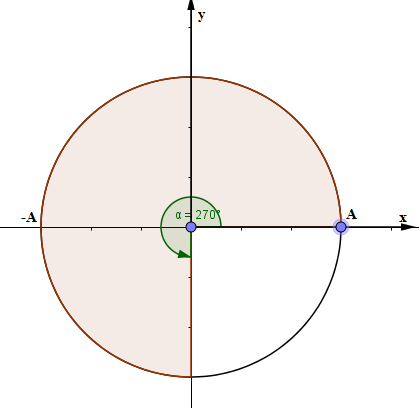
Để vật qua vị trí cân bằng 2 lần => \(\Delta \varphi = \pi + \frac{\pi }{2} = \frac{{3\pi }}{2}\)
\(\begin{array}{l} \to {t_2} = \Delta t = \frac{{\Delta \varphi }}{\omega } = \frac{{\frac{{3\pi }}{2}}}{{\frac{{2\pi }}{T}}} = \frac{{3T}}{4}\\ \to {t_{2012}} = {t_{2010}} + {t_2} = 1005T + \frac{{3T}}{4}\end{array}\)
Một vật dao động điều hòa với phương trình: \(x = 8c{\rm{os}}\left( {2\pi t - \frac{\pi }{6}} \right)cm\). Thời điểm lần thứ \(2018\) kể từ lúc bắt đầu dao động, vật qua vị trí có vận tốc \(v = - 8\pi cm/s\) theo chiều âm là bao nhiêu?
Ta có:
+ Chu kỳ dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1{\rm{s}}\)
+ Tại \(t = 0\) : \(\left\{ \begin{array}{l}x = 8c{\rm{os}}\left( { - \frac{\pi }{6}} \right) = 4\sqrt 3 cm\\v = - 16\pi \sin \left( { - \frac{\pi }{6}} \right) = 8\pi > 0\end{array} \right.\)
+ Tại vị trí có \(v = - 8\pi cm/s\) : \(x = \pm \sqrt {{A^2} - \frac{{{v^2}}}{{{\omega ^2}}}} = \pm \sqrt {{8^2} - \frac{{{{\left( { - 8\pi } \right)}^2}}}{{{{\left( {2\pi } \right)}^2}}}} = \pm 4\sqrt 3 cm\)
Thời điểm lần thứ \(2018\) kể từ lúc bắt đầu dao động, vật qua vị trí có vận tốc \(v = - 8\pi cm/s\) là: \({t_{2018}} = {t_{2016}} + {t_2}\)
+ Ta có, trong một chu kỳ, vật đi qua vị trí có vận tốc \(v = - 8\pi cm/s\) 2 lần
\( \to {t_{2016}} = \frac{{2016}}{2}T = 1008T\)
\({t_2}\) là khoảng thời gian từ lúc bắt đầu đến khi vật đạt vận tốc \(v = - 8\pi cm/s\) lần thứ 2.
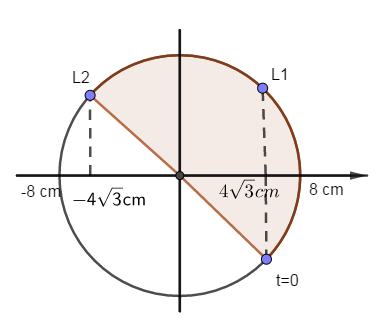
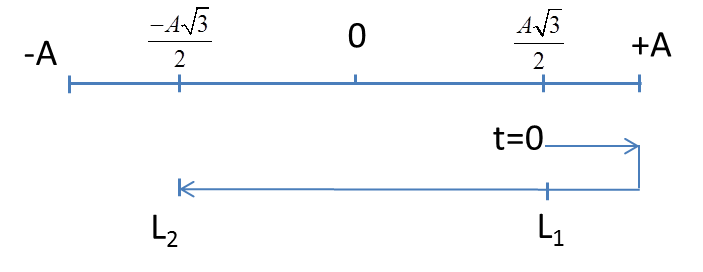
\( \to {t_2} = \frac{{\Delta \varphi }}{\omega } = \frac{\pi }{{\frac{{2\pi }}{T}}} = \frac{T}{2}\)
\( \to {t_{2018}} = {t_{2016}} + {t_2} = 1008T + \frac{T}{2} = 1008,5T = 1008,5{\rm{s}}\)
Một vật dao động điều hòa với phương trình x = Acos(ωt +\(\pi \)/3), chu kì T. Kể từ thời điểm ban đầu thì sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cân bằng theo chiều âm lần thứ 2011?
+ Thời gian vật qua vị trí cân bằng theo chiều âm lần thứ 2011 là: \({t_{2011}} = {t_{2010}} + {t_1}\)
+ Trong 1 chu kì, vật qua vị trí cân bằng theo chiều âm 1 lần
=> \({t_{2010}} = 2010T\)
+ Tại thời điểm ban đầu: \(t = 0\), ta có: \(\left\{ \begin{array}{l}{x_0} = Acos\left( {\frac{\pi }{3}} \right)\\{v_0} = - A\omega \sin \left( {\frac{\pi }{3}} \right)\end{array} \right. \to \left\{ \begin{array}{l}{x_0} = \frac{A}{2}\\{v_0} < 0\end{array} \right.\)
Để vật đi qua vị trí cân bằng theo chiều âm 1 lần thì vật phải đi từ vị trí \(\frac{A}{2}\) về vị trí cân bằng theo chiều âm
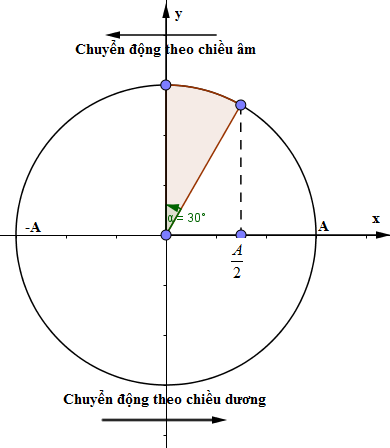
\(\Delta \varphi = \frac{\pi }{6} \to \Delta t = \frac{{\Delta \varphi }}{\omega } = \frac{{\frac{\pi }{6}}}{{\frac{{2\pi }}{T}}} = \frac{T}{{12}}\)
\( \to {t_1} = \frac{T}{{12}}\)
\( \to {t_{2011}} = 2010T + \frac{T}{{12}}\)
Một vật dao động theo phương trình \(x = 3cos\left( {5\pi t - \dfrac{{2\pi }}{3}} \right)cm\). Trong giây đầu tiên vật qua vị trí li độ \(x = 1,5\sqrt 3 cm\) bao nhiêu lần.
Ta có:
+ Chu kỳ dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{5\pi }} = 0,4{\rm{s}}\)
+ Tại $t = 0s$: \(\left\{ \begin{array}{l}x = 3c{\rm{os}}\left( { - \dfrac{{2\pi }}{3}} \right)\\v = - A\omega \sin \left( { - \dfrac{{2\pi }}{3}} \right)\end{array} \right. \to \left\{ \begin{array}{l}{x_0} = - 1,5cm\\{v_0} > 0\end{array} \right.\)
Ta có: \(1{\rm{s}} = 0,8 + 0,2 = 2T + \dfrac{T}{2}\)
+ Trong một chu kỳ, vật đi qua vị trí \(x = 1,5\sqrt 3 cm\) 2 lần
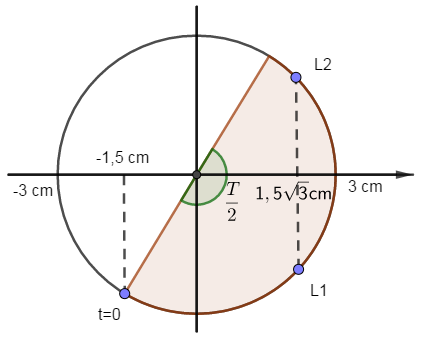
Trong khoảng thời gian \(\dfrac{T}{2}\) vật qua vị trí \(x = 1,5\sqrt 3 cm\) 2 lần kể từ t = 0
=> Trong 1s đầu tiên, vật qua \(x = 1,5\sqrt 3 cm\) số lần là: \(2.2{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}6\) lần
Một chất điểm dao động điều hòa theo phương trình \(x = 3\sin \left( {5\pi t + \dfrac{\pi }{6}} \right)\) (x tính bằng cm, t tính bằng giây). Trong một giây đầu tiên từ thời điểm $t = 0,2s$; chất điểm đi qua vị trí có li độ $x = +1cm$
+ Ta có: \(x = 3sin(5\pi t + \dfrac{\pi }{6}) = 3c{\rm{os}}\left( {5\pi t + \dfrac{\pi }{6} - \dfrac{\pi }{2}} \right) = 3c{\rm{os}}\left( {5\pi t - \dfrac{\pi }{3}} \right)cm\)
+ Chu kỳ dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{5\pi }} = 0,4{\rm{s}}\)
+ Tại $t = 0,2s$: \(\left\{ \begin{array}{l}x = 3c{\rm{os}}\left( {5\pi .0,2 - \dfrac{\pi }{3}} \right)\\v = - A\omega \sin \left( {5\pi .0,2 - \dfrac{\pi }{3}} \right)\end{array} \right. \to \left\{ \begin{array}{l}x = - 1,5cm\\v < 0\end{array} \right.\)
ta có: \(1{\rm{s}} = 0,8 + 0,2 = 2T + \dfrac{T}{2}\)
Trong một chu kỳ, vật đi qua vị trí \( + 1cm\) 2 lần
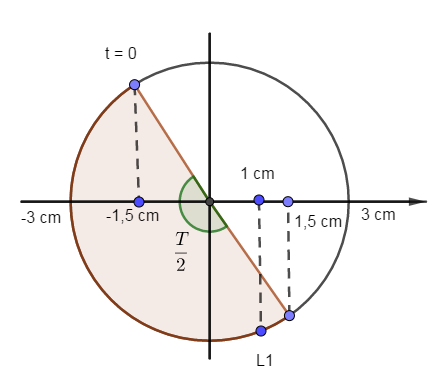
Trong khoảng thời gian \(\dfrac{T}{2}\) vật qua vị trí \( + 1cm\) 1 lần kể từ \(t{\rm{ }} = {\rm{ }}0,2s\)
=> Trong $1s$ đầu tiên kể từ \(t{\rm{ }} = {\rm{ }}0,2s\), vật qua vị trí \( + 1cm\) số lần là: \(2.2{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}5\) lần
Một vật dao động điều hoà với phương trình \(x = 8cos\left( {2\pi t - \dfrac{\pi }{3}} \right)cm\). Tìm số lần vật qua vị trí có độ lớn vận tốc \(8\pi \left( {cm/s} \right)\) trong thời gian \(\dfrac{{35}}{6}s\) tính từ thời điểm gốc.
Ta có:
+ Chu kỳ dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1{\rm{s}}\)
+ Tại $t = 0s$: \(\left\{ \begin{array}{l}x = 8c{\rm{os}}\left( { - \dfrac{\pi }{3}} \right) = 4cm\\v = - A\omega \sin \left( { - \dfrac{\pi }{3}} \right) > 0\end{array} \right.\)
+ Tại vị trí có vật có độ lớn vận tốc \(v = 8\pi \left( {cm/s} \right)\): \(x = \pm \sqrt {{A^2} - \dfrac{{{v^2}}}{{{\omega ^2}}}} = \pm \sqrt {{8^2} - \dfrac{{{{\left( {8\pi } \right)}^2}}}{{{{\left( {2\pi } \right)}^2}}}} = \pm 4\sqrt 3 cm\)
+ Trong một chu kỳ, vật đi qua vị trí có vận tốc độ lớn vận tốc \(v = 8\pi \left( {cm/s} \right)\) $4$ lần
Ta có: \(\dfrac{{{\rm{35}}}}{6}{\rm{s}} = 5s + \dfrac{5}{6}s = 5T + \dfrac{{5T}}{6}\)
Góc quét trong khoảng thời gian \(\dfrac{{5T}}{6}\) từ thời điểm ban đầu: \(\Delta \varphi = \omega \Delta t = \dfrac{{2\pi }}{T}.\dfrac{{5T}}{6} = \dfrac{{5\pi }}{3}\)
Vẽ trên vòng tròn lượng giác ta được:
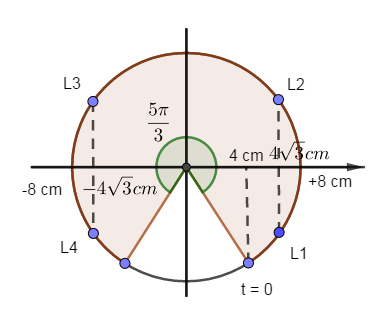
Trong khoảng thời gian \(\dfrac{{5T}}{6}\) vật qua vị trí có vận tốc có độ lớn \(8\pi \left( {cm/s} \right)\) $4$ lần lần kể từ $t = 0$
=> Trong \(\dfrac{{35}}{6}s\) đầu tiên, vật qua vị trí có độ lớn vận tốc \(8\pi cm/s\) số lần là: \(4.5 + 4 = 24\) lần
Một vật dao động điều hoà với phương trình \(x = 4cos\left( {4\pi t + \dfrac{\pi }{6}} \right)cm\). Tìm số lần vật qua vị trí có gia tốc là \(32{\pi ^2}\left( {cm/{s^2}} \right)\) theo chiều âm trong thời gian \(5,75s\) tính từ thời điểm gốc.
Ta có:
Chu kỳ dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\)
Tại $t = 0s$: \(\left\{ \begin{array}{l}x = 4c{\rm{os}}\left( {\dfrac{\pi }{6}} \right) = 2\sqrt 3 cm\\v = - A\omega \sin \left( {\dfrac{\pi }{6}} \right) < 0\end{array} \right.\)
Tại vị trí có \(a = 32{\pi ^2}cm/{s^2} = - {\omega ^2}{x_2} \to {x_2} = - \dfrac{{32{\pi ^2}}}{{{{\left( {4\pi } \right)}^2}}} = - 2cm\)
Trong một chu kỳ, vật đi qua vị trí $-2cm$ theo chiều âm $1$ lần
Ta có: \({\rm{5}}{\rm{,75s}} = 11T + \dfrac{T}{2}\)
Góc quét trong khoảng thời gian \(\dfrac{T}{2}\) kể từ thời điểm ban đầu:
\(\Delta \varphi = \omega .\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{2} = \pi \)
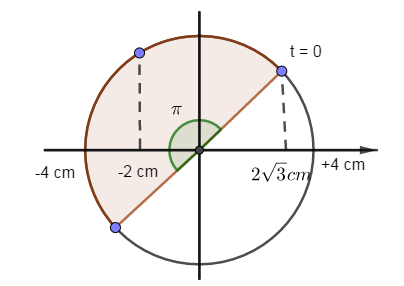
Trong khoảng thời gian \(\dfrac{T}{2}\) vật đi qua vị trí \( - 2cm\) theo chiều âm $1$ lần kể từ $t = 0$
=> Trong \(5,75s\) đầu tiên, vật qua vị trí \( - 2cm\) số lần là: \(11 + 1 = 12\) lần
Một chất điểm đang dao động điều hòa với phương trình \(x = 2cos\left( {2\pi t + \dfrac{\pi }{4}} \right)\;cm\). Tính từ thời điểm ban đầu, chất điểm đi qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) lần thứ \(2020\) vào thời điểm
Chu kì: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1s\)
Ta có: \(x = 2cos\left( {2\pi t + \dfrac{\pi }{4}} \right)\;cm \Rightarrow v = 4\pi .\left( {2\pi t + \dfrac{{3\pi }}{4}} \right)\;cm/s\)
Trong 1 chu kì vật đi qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) hai lần.
Sau \(1009T\) vật đi qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) lần thứ \(2018.\)
Biểu diễn trên VTLG.
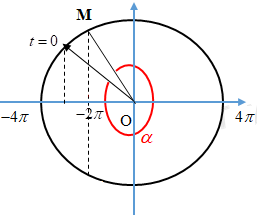
Sau \(1009T\) vật qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) khi góc quét bằng:
\(\alpha = \dfrac{\pi }{4} + \pi + \dfrac{\pi }{2} + \dfrac{\pi }{6} = \dfrac{{23\pi }}{{12}}\)
\( \Rightarrow \Delta t = \alpha .\dfrac{T}{{2\pi }} = \dfrac{{23\pi }}{{12}}.\dfrac{T}{{2\pi }} = \dfrac{{23T}}{{24}}\)
\( \Rightarrow \) Tính từ thời điểm ban đầu, chất điểm đi qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) lần thứ \(2020\) vào thời điểm:
\(t = 1009T + \Delta t = 1009.1 + \dfrac{{23.1}}{{24}} = \dfrac{{24239}}{{24}}\;s\)
Vận tốc của vật dao động điều hoà có phương trình li độ $x = A\cos \left( {\omega t - \dfrac{\pi }{3}} \right)$ có độ lớn cực đại khi:
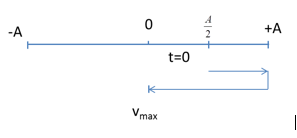
Ta có, vận tốc của vật có độ lớn cực đại khi vật ở VTCB
Tại thời điểm ban đầu t =0 : \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\left( { - \dfrac{\pi }{3}} \right) = \dfrac{A}{2}\\v = - A\omega \sin \left( { - \dfrac{\pi }{3}} \right) > 0\end{array} \right.\)
=> Vận tốc của vật có độ lớn cực đại khi \(t = \dfrac{T}{6} + \dfrac{T}{4} = \dfrac{{5T}}{{12}}\)

