Vật dao động với phương trình \(x = 5cos\left( {4\pi t + \frac{\pi }{6}} \right)cm\). Tìm thời điểm vật qua vị trí cân bằng lần thứ 4 kể từ thời điểm ban đầu.
Trả lời bởi giáo viên
Ta có
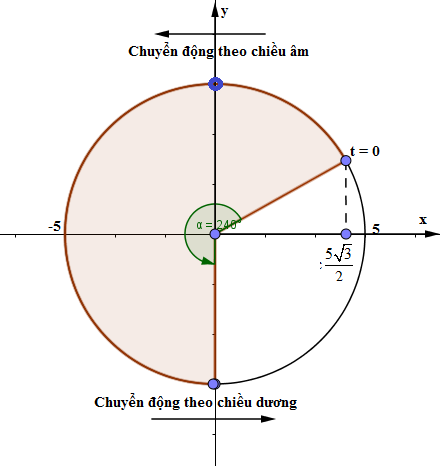
Thời điểm gian vật đi từ vị trí ban đầu đến vị trí cân bằng lần thứ hai vật quét được 1 góc \(\alpha = \frac{{4\pi }}{3}\), vậy áp dụng mối liên hệ gữa góc quét α và khoảng thời gian ∆t thì ta có
\(\alpha = \frac{{4\pi }}{3} = > \Delta t = \frac{\alpha }{\omega } = \frac{{\frac{{4\pi }}{3}.T}}{{2\pi }} = \frac{{2T}}{3}\)
Mặt khác ta thấy từ đường tròn lượng giác trong 1 chu kỳ vật đi qua vị trí cân bằng 2 lần do đó
Thời điểm vật đi qua vị trí vị trí cân bằng lần thứ 4 kể từ thời điểm ban đầu là: \(t = \Delta t + {t_2} = \frac{{2T}}{3} + T = \frac{{5T}}{3}\)
Với \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = \frac{1}{2} = > t = \frac{5}{3}.\frac{1}{2}s = \frac{5}{6}s\)
Hướng dẫn giải:
+ Ứng dụng đường tròn lượng giác và công thức \(\Delta t = \frac{\alpha }{\omega } = \frac{{\alpha .T}}{{2\pi }}\)
+ Sử dụng biểu thức tính chu kì: \(T = \frac{{2\pi }}{\omega }\)

