Một vật dao động điều hoà với phương trình \(x = Acos\left( {\omega t + \dfrac{\pi }{3}} \right)cm\). Biết quãng đường vật đi được trong thời gian 1(s) là 2A và \(\dfrac{2}{3}\)s đầu tiên là $9cm$. Giá trị của $A$ và $\omega$ là:
Trả lời bởi giáo viên
+ Ta có : Vật đi được quãng đường \(2A\) trong khoảng thời gian \(\dfrac{T}{2}\)
\(\dfrac{T}{2} = 1s = > T = 2s = > \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{2} = \pi \,rad/s\)
Vậy ta có \(\dfrac{2}{3}s = \dfrac{T}{3} = > \alpha = \dfrac{{2\pi }}{3}\)
+ Tại thời điểm ban đầu \(t = 0\), ta có: \(\left\{ \begin{array}{l}{x_0} = Acos\left( {\dfrac{\pi }{3}} \right)\\{v_0} = - A\omega \sin \left( {\dfrac{\pi }{3}} \right)\end{array} \right. \to \left\{ \begin{array}{l}{x_0} = \dfrac{A}{2}\\{v_0} < 0\end{array} \right.\)
Ứng dụng vòng tròn lượng giác ta được:
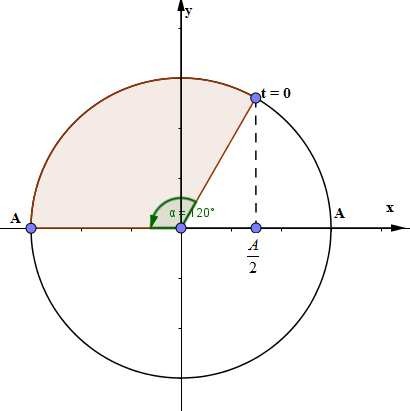
Từ đường tròn lượng giác ta thấy quãng đường vật đi trong \(\dfrac{2}{3}\)s đầu tiên là 9cm tương ứng với $1,5A$ trên đường tròn lượng giác do đó : $1,5 A = 9 => A = 6 cm$
Hướng dẫn giải:
Ứng dụng đường tròn lượng giác và công thức \(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{{\alpha .T}}{{2\pi }}\)

