Một chất điểm đang dao động điều hòa với phương trình \(x = 2cos\left( {2\pi t + \dfrac{\pi }{4}} \right)\;cm\). Tính từ thời điểm ban đầu, chất điểm đi qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) lần thứ \(2020\) vào thời điểm
Trả lời bởi giáo viên
Chu kì: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1s\)
Ta có: \(x = 2cos\left( {2\pi t + \dfrac{\pi }{4}} \right)\;cm \Rightarrow v = 4\pi .\left( {2\pi t + \dfrac{{3\pi }}{4}} \right)\;cm/s\)
Trong 1 chu kì vật đi qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) hai lần.
Sau \(1009T\) vật đi qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) lần thứ \(2018.\)
Biểu diễn trên VTLG.
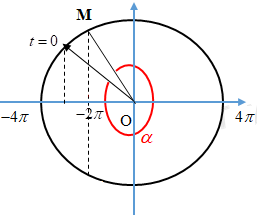
Sau \(1009T\) vật qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) khi góc quét bằng:
\(\alpha = \dfrac{\pi }{4} + \pi + \dfrac{\pi }{2} + \dfrac{\pi }{6} = \dfrac{{23\pi }}{{12}}\)
\( \Rightarrow \Delta t = \alpha .\dfrac{T}{{2\pi }} = \dfrac{{23\pi }}{{12}}.\dfrac{T}{{2\pi }} = \dfrac{{23T}}{{24}}\)
\( \Rightarrow \) Tính từ thời điểm ban đầu, chất điểm đi qua vị trí có vận tốc bằng \( - 2\pi \;cm/s\) lần thứ \(2020\) vào thời điểm:
\(t = 1009T + \Delta t = 1009.1 + \dfrac{{23.1}}{{24}} = \dfrac{{24239}}{{24}}\;s\)
Hướng dẫn giải:
Phương trình của li độ và vận tốc:
\(\left\{ \begin{array}{l}x = Acos\left( {\omega t + \varphi } \right)\;\\v = \omega A.cos\left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\end{array} \right.\)
Sử dụng VTLG cho vận tốc và công thức \(\Delta t = \dfrac{\alpha }{\omega } = \alpha .\dfrac{T}{{2\pi }}\)

