Ôn tập chương 1 - Dao động cơ

Ta có chu kì $T = 2\pi \sqrt {\dfrac{l}{g}}$

$\Rightarrow$ Gia tốc rơi tự do: $g = \dfrac{{4{\pi ^2}l}}{{{T^2}}}$

+ Giá trị trung bình của gia tốc trọng trường: $\overline g  = \dfrac{{4{\pi ^2}\overline l }}{{{{\overline T }^2}}} = \dfrac{{4{\pi ^2}.1}}{{{2^2}}} = 9,87m/{s^2}$

+ Sai số:

$\begin{array}{l}\dfrac{{\Delta g}}{{\overline g }} = \dfrac{{\Delta l}}{{\overline l }} + 2\dfrac{{\Delta T}}{{\overline T }} \Rightarrow \Delta g = \left( {\dfrac{{\Delta l}}{{\overline l }} + 2\dfrac{{\Delta T}}{{\overline T }}} \right)\overline g \\ \Rightarrow \Delta g = \left( {\dfrac{1}{{100}} + 2\dfrac{{0,01}}{2}} \right)9,87 = 0,1974 \approx 0,2m/{s^2}\end{array}$

$\Rightarrow g = \overline g  \pm \Delta g = 9,87 \pm 0,2{\rm{ m/}}{{\rm{s}}^2}$

Chọn C.

Từ đồ thị, ta có gia tốc cực đại là:${a_0} = 25\,\,\left( {cm/{s^2}} \right)$

Chu kì dao động của vật là: $T = 2\,\,\left( s \right) \Rightarrow \omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{2} = \pi \,\,\left( {rad/s} \right)$

Tại thời điểm đầu, gia tốc của vật bằng 0 và đang tăng, pha ban đầu là: $\varphi  =  - \dfrac{\pi }{2}\,\,\left( {rad} \right)$

Phương trình gia tốc của vật là: $a = 25\cos \left( {\pi t - \dfrac{\pi }{2}} \right)\,\,\left( {cm/{s^2}} \right)$

Phương trình li độ của vật là: $x = 2,5\cos \left( {\pi t + \dfrac{\pi }{2}} \right)\,\,\left( {cm} \right)$

Ta có:

+ Tần số góc: $\omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{3,14}} = 2rad/s$

+ Khi chất điểm qua vị trí cân bằng => vận tốc của nó có độ lớn cực đại ${v_{{\rm{max}}}} = \omega A = 2.1 = 2m/s$

Ta có: ${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}$

+ Tại vị trí 1: ${A^2} = x_1^2 + \dfrac{{v_1^2}}{{{\omega ^2}}} \leftrightarrow {A^2} = {3^2} + \dfrac{{40^2}}{{{\omega ^2}}}$ (1)

+ Tại vị trí 2 (vị trí cân bằng): $\left\{ \begin{array}{l}x = 0\\v = \omega A = 50cm/s\end{array} \right.$  (2)

Từ (1) và (2) ta suy ra: $\left\{ \begin{array}{l}\omega  = 10rad/s\\A = 5cm\end{array} \right.$

+ Tại vị trí 3: $\left\{ \begin{array}{l}{x_3} = ?\\{v_3} = 30cm/s\end{array} \right.$

$\begin{array}{l}{A^2} = x_3^2 + \dfrac{{v_3^2}}{{{\omega ^2}}} \leftrightarrow {5^2} = x_3^2 + \dfrac{{{{30}^2}}}{{{{10}^2}}}\\ \to {x_3} =  \pm 4cm\end{array}$ 

Vậy li độ của vật khi có vận tốc ${v_3} = 30cm/s$ là ${x_3} = \pm 4cm$

Ta có phương trình dao động của vật: $x{\rm{ }} = {\rm{ }}6cos(10\pi t + \pi )\left( {cm} \right)$

=> Li độ của vật khi pha dao động bằng $- {60^0}$ là: $x = 6\cos \left( { - {{60}^0}} \right) = 3cm$

Ta có: $T = \dfrac{{\Delta t}}{N} = \dfrac{{60}}{{30}} = 2s$

Phương trình dao động của vật:

$x =  - Asin\left( {\omega t} \right) = A\sin \left( {\omega t + \pi } \right) = Ac{\rm{os}}\left( {\omega t + \pi  - \frac{\pi }{2}} \right) = Ac{\rm{os}}\left( {\omega t + \frac{\pi }{2}} \right)$

Vậy pha ban đầu của dao động: $\varphi  = \frac{\pi }{2}$

Ta có: $a =  - {\omega ^2}x =  - {\left( {2\pi } \right)^2}.3 =  - 120cm/s$

+ Chu kì dao động của vật là: $T = \dfrac{{\Delta t}}{N} = \dfrac{{78,5}}{{50}} = 1,57s$

+ Tần số góc của dao động: $\omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{1,57}} = 4rad/s$

+ Chiều dài quỹ đạo: $L = 2A = 10cm \to A = 5cm$

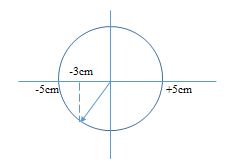
Khi vật qua vị trí có li độ $x =  - 3cm$ theo chiều hướng về vị trí cân bằng thì vận tốc của vật dương (đang chuyển động theo chiều dương)

Áp dụng biểu thức ${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}$

Ta suy ra: $v = \omega \sqrt {{A^2} - {x^2}}  = 4\sqrt {{5^2} - {3^3}}  = 16cm/s = 0,16m/s$ (do vật đang chuyển động theo chiều dương)

+ Gia tốc của vật khi đó: $a =  - {\omega ^2}x =  - {4^2}.\left( { - 3} \right) = 48cm/{s^2} = 0,48m/{s^2}$

Ta có:

$x = asin\omega t + acos\omega t = a\sqrt 2 {\rm{cos}}\left( {\omega t - \frac{\pi }{4}} \right)$

Vậy biên độ dao động của vật là: $a\sqrt 2$

Trong chuyển động dao động điều hòa của một vật thì:

+ Lực, li độ, vận tốc, gia tốc, động năng: thay đổi

Ta có: 

- Li độ: $x=Acos(\omega t + \varphi)$

- Vận tốc: $v=A\omega cos(\omega t + \varphi + \dfrac{\pi}{2})$

- Gia tốc: $a=-{\omega}^2Acos(\omega t + \varphi)$

- Động năng: $W_{đ}=\dfrac{1}{2}mv^2$

+ Biên độ $(A)$, tần số $(f)$, tần số góc $(\omega)$, năng lượng toàn phần $(W)$: không thay đổi

Ta có:

+ Khi vật ở vị trí cân bằng vận tốc đạt giá trị cực đại: ${v_{max}} = \omega A = 62,8cm/s = 0,628m/s$ (1)

+ Khi vật ở vị trí biên, gia tốc có độ lớn cực đại: ${a_{max}} = {\omega ^2}A = 2m/{s^2}$  (2)

Lấy $\dfrac{{{{\left( 1 \right)}^2}}}{{\left( 2 \right)}}$ ta được: $\dfrac{{{\omega ^2}{A^2}}}{{{\omega ^2}A}} = \dfrac{{{{0,628}^2}}}{2} \leftrightarrow A = 0,1972m = 19,72cm \approx 20cm$

Thay vào (1) ta suy ra: $\omega  = \dfrac{{{v_{max}}}}{A} = \dfrac{{0,628}}{{0,1972}} = 3,1846rad/s$

+ Chu kì dao động $T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{3,1846}} = 1,973s \approx 2s$

Ta có chiều dài quỹ đạo của vật dao động điều hòa: $L = 2A = 10cm \to A = 5cm$

Ta có, quãng đường vật đi được trong một chu kì $S = 4A = 16cm \to A = 4cm$

Ta có: $A = \frac{{{l_{max}} - {l_{min}}}}{2} = \frac{{28 - 20}}{2} = 4cm$

Ta có:

+ Li độ, vận tốc, gia tốc biến thiên điều hòa với tần số $f$ , chu kì $T$ và tần số góc $\omega$

+ Động năng, thế năng biến thiên tuần hoàn với tần số $f' = 2f$, chu kì $T' = \frac{T}{2}$ và tần số góc $\omega ' = 2\omega$ 

Ta có cơ năng ${\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2}$

=> Cơ năng tỉ lệ thuận với bình phương biên độ dao động

Hệ thức độc lập A – v – a: ${A^2} = \dfrac{{{v^2}}}{{{\omega ^2}}} + \dfrac{{{a^2}}}{{{\omega ^4}}}$

Ta có: ${x_1} = {A_1}cos\left( {\omega t + \dfrac{\pi }{3}} \right)cm$ và ${x_2} = {A_2}cos\left( {\omega t - \dfrac{\pi }{6}} \right)cm$

Ta suy ra:

+ Cơ năng của dao động 1: ${{\rm{W}}_1} = \dfrac{1}{2}kA_1^2$

Cơ năng của dao động 2: ${{\rm{W}}_2} = \dfrac{1}{2}kA_2^2 = 3{W_1}$

$\to {A_2} = \sqrt 3 {A_1}$

+ Nhận thấy độ lệch pha của hai dao động: $\Delta \varphi  = \dfrac{\pi }{3} - \left( { - \dfrac{\pi }{6}} \right) = \dfrac{\pi }{2}$ => ${x_1},{x_2}$ vuông pha với nhau

Ta suy ra, biên độ dao động tổng hợp: $A = \sqrt {A_1^2 + A_2^2}  = \sqrt {A_1^2 + 3A_1^2}  = 2{A_1}$

=> Cơ năng của dao động tổng hợp: ${\rm{W}} = \dfrac{1}{2}k{A^2} = \dfrac{1}{2}k.{\left( {2{A_1}} \right)^2} = 4.\dfrac{1}{2}kA_1^2 = 4{W_1}$

+ Ta có chu kì dao động của vật là $T = 2s$

=> Trong $2s = 1T$ vật đi được quãng đường $S = 4A = 40cm \to A = 10cm$

+ Tần số góc của dao động : $\omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{2} = \pi \left( {rad/s} \right)$

+ Tại $t = 0:\left\{ \begin{array}{l}x = Acos\varphi  = 0\\v =  - A\sin \varphi  > 0\end{array} \right. \to \varphi  =  - \frac{\pi }{2}$

Vậy phương trình dao động của vật là : $x = 10cos\left( {\pi t - \frac{\pi }{2}} \right)cm$