Câu hỏi:
2 năm trước
Một vật dao động điều hòa trên đoạn thẳng dài \(10cm\) và thực hiện được \(50\) dao động trong thời gian \(78,5\) giây. Tìm vận tốc và gia tốc của vật khi đi qua vị trí có li độ \(x = - 3cm\) theo chiều hướng về vị trí cân bằng.
Trả lời bởi giáo viên
Đáp án đúng: a
+ Chu kì dao động của vật là: \(T = \dfrac{{\Delta t}}{N} = \dfrac{{78,5}}{{50}} = 1,57s\)
+ Tần số góc của dao động: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{1,57}} = 4rad/s\)
+ Chiều dài quỹ đạo: \(L = 2A = 10cm \to A = 5cm\)
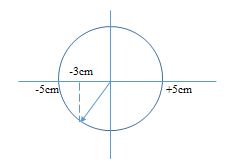
Khi vật qua vị trí có li độ \(x = - 3cm\) theo chiều hướng về vị trí cân bằng thì vận tốc của vật dương (đang chuyển động theo chiều dương)
Áp dụng biểu thức \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
Ta suy ra: \(v = \omega \sqrt {{A^2} - {x^2}} = 4\sqrt {{5^2} - {3^3}} = 16cm/s = 0,16m/s\) (do vật đang chuyển động theo chiều dương)
+ Gia tốc của vật khi đó: \(a = - {\omega ^2}x = - {4^2}.\left( { - 3} \right) = 48cm/{s^2} = 0,48m/{s^2}\)
Hướng dẫn giải:
+ Sử dụng công thức tính chu kì dao đông: \(T = \dfrac{{\Delta t}}{N}\)
+ Sử dụng biểu thức tính tần số góc: \(\omega = \dfrac{{2\pi }}{T}\)
+ Vận dụng biểu thức chiều dài quỹ đạo: \(L = 2A\)
+ Vận dụng hệ thức độc lập A – x – v: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
+ Vận dụng mối liên hệ giữa gia tốc và li độ: \(a = - {\omega ^2}x\)
Câu hỏi khác
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
