Cho đoạn mạch AB theo thứ tự gồm cuộn dây thuần cảm có độ tự cảm \(L\), một đoạn mạch \(X\) và tụ điện có điện dung \(C\) mắc nối tiếp. Gọi \(M\) là điểm nối giữa \(L\) và \(X\), \(N\) là điểm nối giữa \(X\) và \(C\). Đặt vào hai đầu đoạn mạch xoay chiều \(u = {U_0}\cos \omega t\), với ω thỏa mãn điều kiện \(LC{\omega ^2} = 1\). Khi đó điện áp hiệu dụng của đoạn mạch \(AN\) (chứa \(L\) và \(X\)) gấp \(\sqrt 3 \) lần điện áp hiệu dụng của đoạn mạch \(MB\) (chứa \(X\) và \(C\)). Độ lệch pha lớn nhất giữa điện áp của cuộn dây và đoạn mạch \(X\) bằng
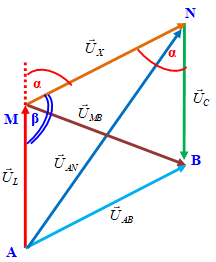
+ \(U_{AN}^2 = 3U_{MB}^2 \to U_L^2 + U_X^2\underbrace { - 2{U_L}{U_X}{\rm{cos}}\beta }_{ - c{\rm{os}}\beta = c{\rm{os}}\alpha } = 3(\underbrace {U_C^2}_{U_L^2} + U_X^2 - 2\underbrace {{U_C}}_{{U_L}}{U_X}{\rm{cos}}\alpha {\rm{)}}\)
=> \(4{U_L}{U_X}{\rm{cos}}\alpha = U_L^2 + U_X^2 \ge 2{U_L}.{U_X}\) (Theo cosi)
=> \({\rm{cos}}\alpha \ge \dfrac{1}{2} \to \)\(\alpha \le \dfrac{\pi }{3}\)
Một đoạn mạch gồm tụ điện mắc nối tiếp với một cuộn dây. Điện áp giữa hai đầu cuộn dây lệch pha \(\dfrac{\pi }{3}\) so với cường độ dòng điện và lệch pha \(\dfrac{\pi }{2}\) so với điện áp hai đầu đoạn mạch. Biết điện áp hiệu dụng giữa hai đầu đoạn mạch bằng \(100V\), khi đó điện áp hiệu dụng trên tụ điện và trên cuộn dây lần lượt là:
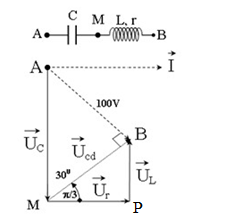
Từ giản đồ, ta có:
+ Xét \(\Delta AMB\) vuông tại B, có:
\(\begin{array}{l}\tan {30^0} = \dfrac{{AB}}{{MB}} = \dfrac{U}{{{U_{cd}}}}\\ \Rightarrow {U_{cd}} = \dfrac{U}{{\tan {{30}^0}}} = \dfrac{{100}}{{\dfrac{1}{{\sqrt 3 }}}} = 100\sqrt 3 V\end{array}\)
\(\begin{array}{l}\sin {30^0} = \dfrac{{AB}}{{AM}} = \dfrac{U}{{{U_C}}}\\ \Rightarrow {U_C} = \dfrac{U}{{\sin {{30}^0}}} = \dfrac{{100}}{{\dfrac{1}{2}}} = 200V\end{array}\)
Mạch điện gồm cuộn dây mắc nối tiếp với tụ điện C. Đặt vào hai đầu đoạn mạch điện áp xoay chiều \(200V - 50Hz\) thì điện áp hai đầu cuộn dây và hai đầu tụ điện có cùng giá trị hiệu dụng nhưng lệch pha nhau góc \({120^0}\). Điện áp hiệu dụng trên tụ là:
Ta có:
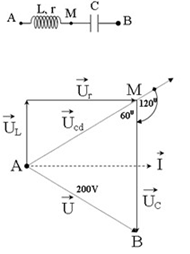
Từ giản đồ véc-tơ,
+ Xét \(\Delta AMB\) có \(AM = MB\) và \(\widehat {AMB} = {60^0}\)
=> \(\Delta AMB\) là tam giác đều
\( \Rightarrow {U_{cd}} = {U_C} = U = 200V\)
Một đoạn mạch xoay chiều AB gồm điện trở thuần R mắc nối tiếp với cuộn dây. Điện áp hiệu dụng ở hai đầu điện trở, cuộn dây và hai đầu đoạn mạch lần lượt là \(70V,150V\) và \(200V\). Hệ số công suất của cuộn dây là:
Ta có:
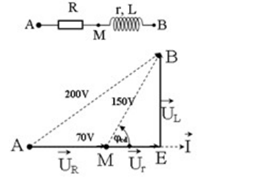
Từ giản đồ ta có:
\(\begin{array}{l}A{B^2} = A{M^2} + M{B^2} - 2AM.MB.cos\left( {\pi - {\varphi _{cd}}} \right)\\ \Leftrightarrow A{B^2} = A{M^2} + M{B^2} + 2AM.MB.cos{\varphi _{cd}}\\ \Rightarrow cos{\varphi _{cd}} = \dfrac{{A{B^2} - A{M^2} - M{B^2}}}{{2AM.MB}} = \dfrac{{{{200}^2} - {{70}^2} - {{150}^2}}}{{2.70.150}} = \dfrac{3}{5} = 0,6\end{array}\)
Đoạn mạch điện xoay chiều gồm điện trở thuần R mắc nối tiếp với cuộn dây. Điện áp hiệu dụng ở hai đầu điện trở, cuộn dây và hai đầu đoạn mạch lần lượt là \(35V,85V\) và \(75\sqrt 2 V\). Cuộn dây tiêu thụ công suất \(40W\). Tổng điện trở thuần của toàn mạch có giá trị là bao nhiêu?
Ta có:
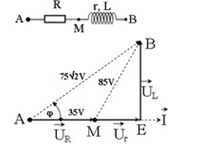
Từ giản đồ, xét tam giác MAB, có:
\(\begin{array}{l}M{B^2} = A{B^2} + A{M^2} - 2AB.AM.cos\varphi \\ \Rightarrow cos\varphi = \dfrac{{A{B^2} + A{M^2} - M{B^2}}}{{2AB.AM}}\\ = \dfrac{{{{\left( {75\sqrt 2 } \right)}^2} + {{\left( {35} \right)}^2} - {{85}^2}}}{{2.75\sqrt 2 .35}} = \dfrac{1}{{\sqrt 2 }}\end{array}\)
Trong \(\Delta AEB\) , có:
\(cos\varphi = \dfrac{{AE}}{{AB}} = \dfrac{{{U_{R + r}}}}{{75\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }} \Rightarrow {U_{R + r}} = 75V\)
Mà \({U_R} = 35V \Rightarrow {U_r} = 75 - 35 = 40V\)
+ Theo đầu bài ta có, cuộn dây tiêu thụ công suất:
\(\begin{array}{l}P = {I^2}r = I.{U_r} = 40W\\ \Rightarrow I = \dfrac{P}{{{U_r}}} = \dfrac{{40}}{{40}} = 1A\end{array}\)
+ Lại có : \(R + r = \dfrac{{{U_{R + r}}}}{I} = \dfrac{{75}}{1} = 75\Omega \)
Một đoạn mạch xoay chiều gồm cuộn dây mắc nối tiếp với tụ điện. Độ lệch pha giữa cường độ dòng điện trong mạch và điện áp hai đầu mạch là \(\dfrac{\pi }{3}\). Điện áp hiệu dụng giữa hai đầu tụ điện bằng \(\sqrt 3 \) lần điện áp hai đầu cuộn dây. Độ lệch pha của điện áp giữa hai đầu cuộn dây so với cường độ dòng điện trong mạch là:
Ta có:
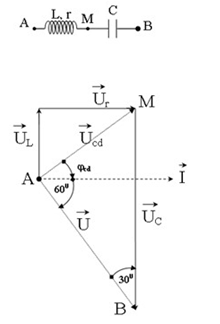
Xét \(\Delta AMB\) , có:
\(\begin{array}{l}\dfrac{{MB}}{{\sin \left( {{\varphi _{cd}} + {{60}^0}} \right)}} = \dfrac{{AM}}{{\sin {{30}^0}}}\\ \Leftrightarrow \dfrac{{{U_C}}}{{\sin \left( {{\varphi _{cd}} + {{60}^0}} \right)}} = \dfrac{{{U_{cd}}}}{{\sin {{30}^0}}}\\ \Leftrightarrow \dfrac{{\sqrt 3 {U_{cd}}}}{{\sin \left( {{\varphi _{cd}} + {{60}^0}} \right)}} = \dfrac{{{U_{cd}}}}{{\dfrac{1}{2}}}\\ \Rightarrow \sin \left( {{\varphi _{cd}} + {{60}^0}} \right) = \dfrac{{\sqrt 3 }}{2}\\ \Rightarrow \left[\begin{array}{l}{\varphi _{cd}} + {60^0} = {60^0} + k2\pi \\{\varphi _{cd}} + {60^0} = \left( {{{180}^0} - {{60}^0}} \right) + k2\pi \end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}{\varphi _{cd}} = 0 + k2\pi \left( {loai} \right)\\{\varphi _{cd}} = {60^0} + k2\pi \end{array} \right.\end{array}\)
\( \Rightarrow {\varphi _{cd}} = {60^0} = \dfrac{\pi }{3}\)
Đặt điện áp \(100V - 25Hz\) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn dây có điện trở thuần \(r\), cuộn cảm có độ tự cảm \(L\) và tụ điện có điện dung \(C = \dfrac{{0,1}}{\pi }mF\). Biết điện áp hai đầu cuộn dây sớm pha hơn dòng điện trong mạch là \(\dfrac{\pi }{6}\), đồng thời điện áp hiệu dụng hai đầu cuộn dây gấp đôi trên tụ điện. Công suất tiêu thụ của toàn mạch là:
Ta có:
+ Dung kháng của mạch: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .25.\dfrac{{0,1}}{\pi }{{.10}^{ - 3}}}} = 200\Omega \)
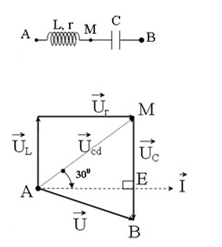
Từ giản đồ,
Xét \(\Delta AME\) , có:
\(\begin{array}{l}\sin \widehat {MAE} = \dfrac{{ME}}{{AM}} \Leftrightarrow \sin {30^0} = \dfrac{{ME}}{{AM}}\\ \Rightarrow ME = AM\sin {30^0} = \dfrac{{AM}}{2} = \dfrac{{{U_{cd}}}}{2}\end{array}\)
Mà theo đầu bài ta có, \({U_{cd}} = 2{U_C}\)
Ta suy ra: \(ME = {U_C}\) hay \(E \equiv M\)
\( \Rightarrow {U_L} = {U_C}\) => Mạch cộng hưởng \( \Rightarrow {U_R} = U = 100V\)
+ Ta có:
\(\begin{array}{l}\tan {30^0} = \dfrac{{{U_C}}}{{{U_R}}} \Rightarrow {U_C} = {U_R}\tan {30^0}\\ \Rightarrow {Z_C} = R.\tan {30^0}\\ \Rightarrow R = \dfrac{{{Z_C}}}{{\tan {{30}^0}}} = \dfrac{{200}}{{\dfrac{1}{{\sqrt 3 }}}} = 200\sqrt 3 \Omega \end{array}\)
+ Công suất của mạch khi đó: \(P = {P_{max}} = \dfrac{{{U^2}}}{R} = \dfrac{{{{100}^2}}}{{200\sqrt 3 }} = \dfrac{{50}}{{\sqrt 3 }}{\rm{W}}\)
Trên đoạn mạch xoay chiều không phân nhánh có 4 điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có cuộn cảm thuần, giữa hai điểm M và N chỉ có điện trở thuần, giữa hai điểm N và B chỉ có tụ điện. Điện áp hiệu dụng giữa hai điểm A và N là \(400{\rm{ }}V\) và điện áp hiệu dụng giữa hai điểm M và B là \(300{\rm{ }}V\). Điện áp tức thời trên đoạn AN và trên đoạn MB lệch pha nhau \({90^0}\). Biết cường độ dòng điện hiệu dụng trong mạch có giá trị \(3\sqrt 2 A\). Giá trị của điện trở R là:
Vẽ lại mạch điện và vẽ giản đồ véctơ, ta được:
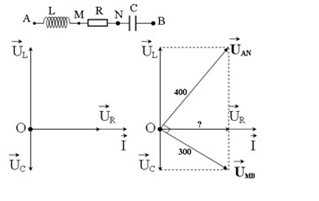
Từ giản đồ véctơ, ta có: \(\dfrac{1}{{U_R^2}} = \dfrac{1}{{U_{AN}^2}} + \dfrac{1}{{U_{MB}^2}} = \dfrac{1}{{{{300}^2}}} + \dfrac{1}{{{{400}^2}}} \to {U_R} = 240V\)
=> Điện trở \(R = \dfrac{{{U_R}}}{I} = \dfrac{{240}}{{3\sqrt 2 }} = 40\sqrt 2 \Omega \)
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N, B. Giữa hai điểm A và M chỉ có cuộn cảm thuần, giữa hai điểm M và N chỉ có điện trở thuần, giữa hai điểm N và B chỉ có tụ điện. Điện áp hiệu dụng giữa hai điểm A và M là \(150V\) và điện áp hiệu dụng giữa hai điểm N và B là \(\dfrac{{200}}{3}V\). Điện áp tức thười trên đoạn AN và trên đoạn MB lệch pha nhau \({90^0}\). Biết cường độ dòng điện hiệu dụng trong mạch có giá trị \(2A\). Điện trở R có giá trị là:
Vẽ lại mạch điện và vẽ giản đồ véctơ, ta được:
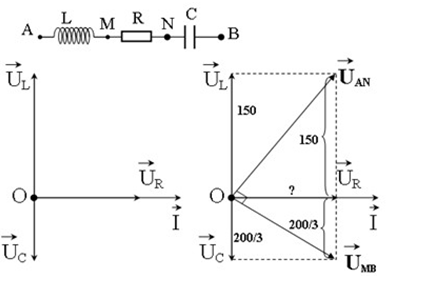
Từ giản đồ véctơ, xét tam giác vuông \({U_{AN}}O{U_{MB}}\) , ta có:
Đường cao trong tam giác vuông: \(U_R^2 = {U_L}{U_C} = 150.\dfrac{{200}}{3} \to {U_R} = 100V\)
=> Điện trở R: \(R = \dfrac{{{U_R}}}{I} = \dfrac{{100}}{2} = 50\Omega \)
Trên đoạn mạch xoay chiều không phân nhánh có 4 điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có điện trở thuần R, giữa hai điểm M và N chỉ có cuộn dây, giữa hai điểm N và B chỉ có tụ điện. Cuộn dây điện trở thuần \(r{\rm{ }} = {\rm{ }}0,5R\). Điện áp hiệu dụng trên đoạn AN là \(U\sqrt 3 \) và trên đoạn MB là U. Điện áp tức thời trên đoạn AN và trên đoạn MB lệch pha nhau \({90^0}\). Hệ số công suất của đoạn mạch AN là:
Vẽ giản đồ véctơ, ta được:
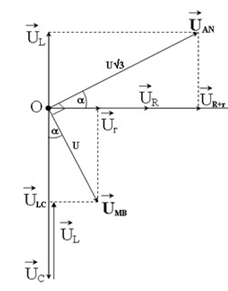
Từ giản đồ véctơ, ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\sin \alpha = \dfrac{{{U_r}}}{{{U_{MB}}}} = \dfrac{{{U_r}}}{U}\\{\rm{cos}}\alpha {\rm{ = }}\dfrac{{{U_{R + r}}}}{{{U_{AN}}}} = \dfrac{{{U_{R + r}}}}{{U\sqrt 3 }} = \dfrac{{3{U_r}}}{{U\sqrt 3 }}\end{array} \right.\\ \to \tan \alpha = \dfrac{{\sqrt 3 }}{3} \to \alpha = {30^0}\\ \Rightarrow cos\alpha = cos{30^0} = \dfrac{{\sqrt 3 }}{2}\end{array}\)
Vậy hệ số công suất của đoạn mạch AN là: \(cos\alpha = \dfrac{{\sqrt 3 }}{2}\)
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, B, C và D. Giữa hai điểm A và B chỉ có tụ điện, giữa hai điểm B và C chỉ có điện trở thuần, giữa 2 điểm C và D chỉ có cuộn cảm thuần cảm. Điện áp hiệu dụng giữa hai điểm A và D là \(100\sqrt 3 V\) và cường độ hiệu dụng chạy qua mạch là \(1{\rm{ }}\left( A \right)\). Điện áp tức thời trên đoạn AC và trên đoạn BD lệch pha nhau \({60^0}\) và giá trị hiệu dụng bằng nhau. Cảm kháng của mạch có giá trị là:
Vẽ lại mạch điện và vẽ giản đồ véctơ, ta được:
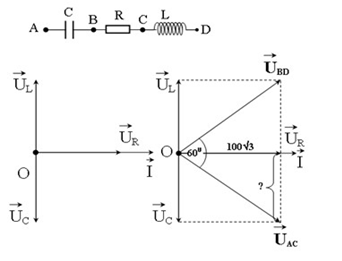
Ta có: \({U_{AC}} = {\rm{ }}{U_{BD}}\) và góc \({U_{BD}}O{U_{AC}}\) bằng \({60^0}\)
=> Tam giác \({U_{BD}}O{U_{AC}}\) là tam giác đều (do tam giác cân có 1 góc = \({60^0}\) là tam giác đều)
Từ giản đồ véctơ, ta có: \({U_L} = {U_C} = \dfrac{{{U_R}}}{{\sqrt 3 }}\) => Mạch cộng hưởng
\(\begin{array}{l} \Rightarrow {U_R} = U = 100\sqrt 3 \,V\\ \Rightarrow {U_L} = \frac{{{U_R}}}{{\sqrt 3 }} = \frac{{100\sqrt 3 }}{{\sqrt 3 }} = 100V\\ \Rightarrow {Z_L} = \frac{{{U_L}}}{I} = 100\Omega \end{array}\)
Mạch điện xoay chiều nối tiếp Ab theo đúng thứ tự gồm cuộn dây thuần cảm có hệ số tự cảm L, điện trở thuần R và tụ điện có điện dung C. Cho biết điện áp hiệu dụng \({U_{RC}} = 0,75{U_{RL}}\) và \({R^2} = \dfrac{L}{C}\). Hệ số công suất của đoạn mạch AB có giá trị là:
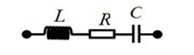
Ta có:
\(\begin{array}{l}{R^2} = \dfrac{L}{C} \Leftrightarrow \dfrac{L}{R}.\dfrac{1}{{RC}} = 1\\ \Leftrightarrow \dfrac{{\omega L}}{R}\dfrac{1}{{\omega C.R}} = 1 \Leftrightarrow \dfrac{{{Z_L}}}{R}\dfrac{{{Z_C}}}{R} = 1\\ \Leftrightarrow \dfrac{{{Z_L}}}{R}.\dfrac{{\left( { - {Z_C}} \right)}}{R} = - 1\\ \Leftrightarrow \tan {\varphi _{RL}}.\tan {\varphi _{RC}} = - 1\end{array}\)
\( \Rightarrow {\varphi _{RL}} - {\varphi _{RC}} = \dfrac{\pi }{2}\) hay \({U_{RL}} \bot {U_{RC}}\)
Đặt \({U_{RL}} = a \Rightarrow {U_{RC}} = 0,75a\)
Vẽ giản đồ véc-tơ, ta được:
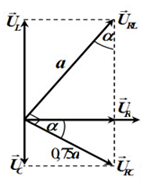
Từ giản đồ, ta có:
\(\begin{array}{l}\dfrac{1}{{U_R^2}} = \dfrac{1}{{U_{RL}^2}} + \dfrac{1}{{U_{RC}^2}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {0,75a} \right)}^2}}} = \dfrac{{25}}{{9{a^2}}}\\ \Rightarrow {U_R} = \dfrac{{3a}}{5}\end{array}\)
Xét: \(\sin \alpha = \dfrac{{{U_R}}}{{{U_{RL}}}} = \dfrac{{\dfrac{{3a}}{5}}}{a} = \dfrac{3}{5}\)
Mặt khác, \(\sin \alpha = \dfrac{{{U_C}}}{{{U_{RC}}}} \Rightarrow {U_C} = {U_{RC}}.\sin \alpha = 0,75a.\dfrac{3}{5} = 0,45a\)
Xét: \(cos\alpha = \dfrac{{{U_R}}}{{{U_{RC}}}} = \dfrac{{\dfrac{{3a}}{5}}}{{0,75a}} = \dfrac{4}{5}\)
Lại có, \(cos\alpha = \dfrac{{{U_L}}}{{{U_{RL}}}} \Rightarrow {U_L} = {U_{RL}}.cos\alpha = a.\dfrac{4}{5} = 0,8a\)
+ Hiệu điện thế hiệu đụng trên mạch: \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} = \sqrt {{{\left( {\dfrac{{3a}}{5}} \right)}^2} + {{\left( {0,8a - 0,45a} \right)}^2}} = 0,695a\)
+ Hệ số công suất của đoạn mạch: \(cos\varphi = \dfrac{{{U_R}}}{U} = \dfrac{{\dfrac{3}{5}a}}{{0,695a}} = 0,864\)
Đặt điện áp xoay chiều \(u = 80c{\rm{os}}\omega {\rm{t}}\left( V \right)\)vào hai đầu đoạn mạch nối tiếp gồm điện trở R, cuộn cảm có độ tự cảm L, có điện trở thuần r và tụ điện C thì công suất tiêu thụ của mạch là \(40W\). Biết điện áp hiệu dụng trên điện trở, trên cuộn cảm và trên tụ điện lần lượt là 25V, 25V và 60V. Tổng giá trị điện trở trong mạch \(\left( {R + r} \right)\) là:
Vẽ lại mạch điện và vẽ giản đồ véctơ, ta được:
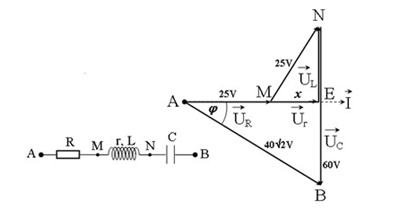
Từ giản đồ véctơ, ta có:
\(\begin{array}{l}N{E^2} = M{N^2} - M{E^2} = 625 - {x^2}\\ \to EB = 60 - \sqrt {625 - {x^2}} \\A{B^2} = A{E^2} + E{B^2} \leftrightarrow {\left( {40\sqrt 2 } \right)^2} = {\left( {25 + x} \right)^2} + {\left( {60 - \sqrt {625 - {x^2}} } \right)^2}\\ \to ... \to 120\sqrt {625 - {x^2}} = 1650 + 50{\rm{x}}\\ \to {\rm{12}}\sqrt {625 - {x^2}} = 165 + 5{\rm{x}}\\ \to {\rm{144}}\left( {625 - {x^2}} \right) = {\left( {165 + 5{\rm{x}}} \right)^2}\\ \to \left[ \begin{array}{l}x = 15\\x = - 24,76\end{array} \right.\\ \to x = 15 \Rightarrow AE = 40{\rm{V}}\\P = UIc{\rm{os}}\varphi {\rm{ = I}}{\rm{.AE}} \to I = \dfrac{P}{{AE}} = 1A\\ \to \left\{ \begin{array}{l}r = \dfrac{{{U_r}}}{I} = \dfrac{{15}}{1} = 15\Omega \\R = \dfrac{{{U_R}}}{I} = \dfrac{{25}}{1} = 25\Omega \end{array} \right.\\ \Rightarrow R + r = 25 + 15 = 40\Omega \end{array}\)
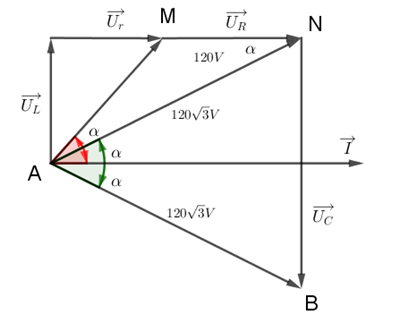
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có điện trở \(R\), giữa hai điểm M và N có cuộn cảm có điện trở thuần \(r = 0,5R\)và độ tự cảm \(L = \dfrac{1}{\pi }H\), giữa hai điểm N và B chỉ có tụ điện có điện dung \(C = \dfrac{{50}}{\pi }\mu F\). Điện áp hiệu dụng trên đoạn AN là \(200V\). Điện áp trên đoạn MN lệch pha với điện áp trên AB là \(\dfrac{\pi }{2}\). Biểu thức điện áp trên \(AB\) là \({u_{AB}} = {U_0}cos\left( {100\pi t + \dfrac{\pi }{{12}}} \right)V\). Biểu thức điện áp trên NB là:
Ta có:
+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{\pi } = 100\Omega \)
Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{50}}{\pi }{{.10}^{ - 6}}}} = 200\Omega = 2{Z_L}\)
Vẽ trên giản đồ, ta được:
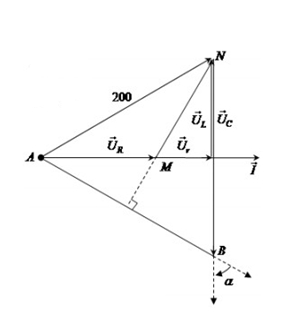
Ta có:
\(r = 0,5R \Rightarrow {U_r} = 0,5{U_R}\)
Lại có \({Z_C} = 2{Z_L} \Rightarrow {U_C} = 2{U_L}\)
Ta suy ra: \(\Delta ANB\) là \(\Delta \) đều
\(\begin{array}{l} \Rightarrow NB = AN \Leftrightarrow {U_C} = {U_{AN}} = 200V\\ \Rightarrow {U_{0C}} = 200\sqrt 2 V\end{array}\)
\(\alpha = \widehat {ABN} = {60^0}\) (2 góc đối đỉnh)
Từ giản đồ, ta có điện áp trên đoạn NB trễ pha so với điện áp trên AB một góc \(\alpha = {60^0} = \dfrac{\pi }{3}\)
\(\begin{array}{l} \Rightarrow {\varphi _{AB}} - {\varphi _{NB}} = \dfrac{\pi }{3}\\ \Rightarrow {\varphi _{NB}} = {\varphi _{AB}} - \dfrac{\pi }{3} = \dfrac{\pi }{{12}} - \dfrac{\pi }{3} = - \dfrac{\pi }{4}\left( {rad} \right)\end{array}\)
=> Phương trình điện áp trên đoạn NB: \({u_{NB}} = 200\sqrt 2 cos\left( {100\pi t - \dfrac{\pi }{4}} \right)V\)
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa 2 điểm A và M chỉ có cuộn dây, giữa 2 điểm M và N chỉ có điện trở thuần R, giữa 2 điểm N và B chỉ có tụ điện. Điện áp hiệu dụng trên AB, AN và MN thỏa mãn hệ thức \({U_{AB}} = {U_{AN}} = {U_{MN}}\sqrt 3 = 120\sqrt 3 V\). Dòng điện hiệu dụng dụng trong mạch có giá trị là \(2\sqrt 2 A\). Điện áp tức thời trên đoạn AN và trên đoạn AB lệch pha nhau một góc đúng bằng góc lệch pha giữa điện áp tức thời trên AM và dòng điện. Cảm kháng của cuộn dây có giá trị là:
Ta có:
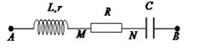
Gọi độ lệch pha giữa điện áp tức thời trên đoạn AN và trên đoạn AB là \(2\alpha \)
=> góc lệch pha giữa điện áp tức thời trên AM và dòng điện cũng là \(2\alpha \)
Vẽ trên giản đồ véc-tơ ta được:
Ta có:
Tam giác AMN cân tại M (do \(\widehat {MAN} = \widehat {MNA}\) )
\( \Rightarrow AM = MN = 120\)
Xét \(\Delta AMN\), có:
\(\begin{array}{l}A{M^2} = M{N^2} + A{N^2} - 2MN.AN.cos\alpha \\ \Leftrightarrow {120^2} = {120^2} + {\left( {120\sqrt 3 } \right)^2} - 2.120.120\sqrt 3 .cos\alpha \\ \Rightarrow cos\alpha = \dfrac{{\sqrt 3 }}{2}\\ \Rightarrow \alpha = {30^0}\end{array}\)
+ Xét \(\Delta ANI\), có:
\(\begin{array}{l}\sin \alpha = \dfrac{{NI}}{{AN}} = \dfrac{{{U_L}}}{{AN}}\\ \Rightarrow {U_L} = AN.\sin \alpha = 120\sqrt 3 .\sin 30 = 60\sqrt 3 V\end{array}\)
+ Cảm kháng: \({Z_L} = \dfrac{{{U_L}}}{I} = \dfrac{{60\sqrt 3 }}{{2\sqrt 2 }} = 15\sqrt 6 \Omega \)
Một mạch điện xoay chiều nối tiếp AB gồm: đoạn AN chứa tụ điện có điện dung C nối tiếp với điện trở thuần R, đoạn NB là cuộn dây có hệ số tự cảm L và điện trở thuần r. Điện áp hiệu dụng trên các đoạn AN, NB và AB lần lượt là \(80V,170V\) và \(150V\). Cường độ dòng điện hiệu dụng qua mạch là \(1A\). Hệ số công suất của đoạn AN là \(0,8\). Tổng điện trở thuần của toàn mạch có giá trị là:
Dựa vào các dữ kiện đề bài, vẽ giản đồ ta được:
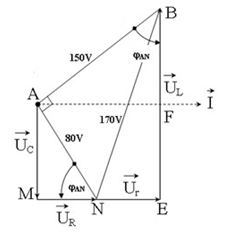
Ta có: \(\Delta AMN\) vuông
\( \Rightarrow cos{\varphi _{AN}} = 0,8\)
\( \Rightarrow \sin {\varphi _{AN}} = \sqrt {1 - co{s^2}{\varphi _{AN}}} = \sqrt {1 - 0,{8^2}} = 0,6\)
Xét \(\Delta ANB\), có \({80^2} + {150^2} = {170^2} \Leftrightarrow A{N^2} + A{B^2} = N{B^2}\)
\( \Rightarrow \Delta ANB\) vuông tại A
+ Xét \(\Delta BAN\), có:
\(\widehat {NBA} + \widehat {BNA} = {90^0}\) (1)
+ Xét \(\Delta NEB\), có:
\(\widehat {EBN} + \widehat {ENB} = {90^0}\) (2)
Lấy (1) + (2), ta được:
\(\begin{array}{l}\left( {\widehat {NBA} + \widehat {EBN}} \right) + \left( {\widehat {BNA} + \widehat {ENB}} \right) = {180^0}\\ \Leftrightarrow \widehat {EBA} + \widehat {ENA} = {180^0}\end{array}\)
Mặt khác, ta có \(\widehat {ANE} = {180^0} - \widehat {ANM} = {180^0} - {\varphi _{AN}}\)
\(\begin{array}{l} \Rightarrow \widehat {EBA} + {180^0} - \widehat {ANM} = {180^0}\\ \Rightarrow \widehat {ABE} = \widehat {ANM} = {\varphi _{AN}}\end{array}\)
+ Xét \(\Delta ABF\), có:
\(\begin{array}{l}\sin {\varphi _{AN}} = \dfrac{{AF}}{{AB}} = \dfrac{{{U_{R + r}}}}{U}\\ \Rightarrow {U_{R + r}} = U.\sin {\varphi _{AN}} = 150.0,6 = 90V\end{array}\)
Lại có: \(I = \dfrac{{{U_{R + r}}}}{{R + r}} \Rightarrow R + r = \dfrac{{{U_{R + r}}}}{I} = \dfrac{{90}}{1} = 90\Omega \)
Một mạch điện xoay chiều nối tiếp gồm tụ điện có điện dung C, điện trở thuần R và cuộn dây có độ tự cảm L có điện trở thuần r. Dùng vôn kế có điện trở rất lớn lần lượt đo hai đầu điện trở, hai đầu cuộn dây và hai đầu đoạn mạch thì số chỉ lần lượt là \(50V,30\sqrt 2 V\) và \(80V\). Biết điện áp tức thời trên cuộn dây sớm pha hơn dòng điện một góc \(\dfrac{\pi }{4}\). Điện áp hiệu dụng trên tụ là:
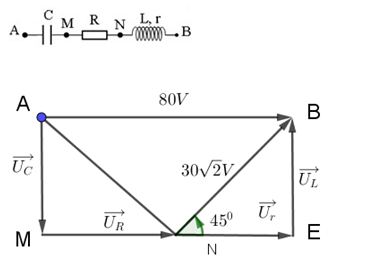
Từ giản đồ, ta có:
\(\Delta ENB\) vuông cân tại E (tam giác vuông có 1 góc bằng \({45^0}\))
\( \Rightarrow BE = NE = 30V\)
\(ME = MN + NE = 80V = AB\)
\( \Rightarrow \)tứ giác AMNB là hình chữ nhật
\( \Rightarrow {U_C} = AM = BE = 30V\)
Mạch điện như hình vẽ, các vôn kế: V1 chỉ 75V, V2 chỉ 125V,
\({u_{MP}} = 100\sqrt 2 {\rm{cos}}\left( {100\pi t} \right)V\).
Cuộn cảm có điện trở. Cho
\({R_A} = {\rm{ }}0,{\rm{ }}{R_{V1}} = {\rm{ }}{R_{V2}} = \infty .\)
Biểu thức điện áp uMN là:
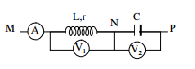
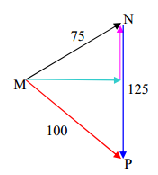
Nhận xét:
\(U_{NP}^2 = U_{MP}^2 + U_{MN}^2 \to {U_{MN}} \bot {U_{MP}}\)
Ta có:
\({U_{0MN}} = {V_1}\sqrt 2 = 75\sqrt 2 V\)
\({U_{MN}} \bot {U_{MP}} \to {\varphi _{{u_{MN}}}} - {\varphi _{MP}} = \frac{\pi }{2} \to {\varphi _{{u_{MN}}}} = {\varphi _{MP}} + \frac{\pi }{2} = \frac{\pi }{2}\)
=> Biểu thức điện áp:
\({u_{MN}} = 75\sqrt 2 {\rm{cos}}\left( {100\pi t + \frac{\pi }{2}} \right)V\)
Đặt điện áp \(u = 220\sqrt 2 {\rm{cos100}}\pi {\rm{t}}\left( V \right)\) vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm cuộn cảm thuần L mắc nối tiếp với điện trở thuần R, đoạn MB chỉ có tụ điện C. Biết điện áp giữa hai đầu đoạn mạch AM và điện áp giữa hai đầu đoạn mạch MB có giá trị hiệu dụng bằng nhau nhưng lệch pha nhau góc \(\frac{{2\pi }}{3}\). Điện áp hiệu dụng giữa hai đầu đoạn mạch AM bằng:
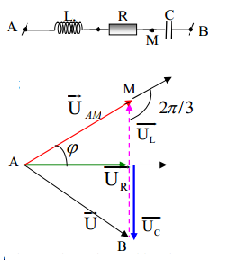
Ta có: Tam giác AMB là tam giác đều
=> UAB = UAM = 220V
Đoạn mạch điện xoay chiều gồm điện trở thuần R = 30Ω mắc nối tiếp với cuộn dây. Điện áp hiệu dụng hai đầu cuộn dây là 120V. Dòng điện trong mạch lệch pha \(\dfrac{\pi }{6}\) so với điện áp hai đầu đoạn mạch và lệch pha \(\dfrac{\pi }{3}\) so với điện áp hai đầu cuộn dây. Cường độ dòng điện hiệu dụng qua mạch bằng:
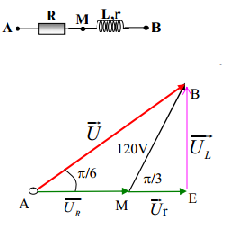
Ta có mạch điện được vẽ lại như trên.
Ta có: \(\widehat {BAM} = \dfrac{\pi }{6};\\\widehat {AMB} = \pi - \widehat {BMI} = \pi - \dfrac{\pi }{3} = \dfrac{{2\pi }}{3} \\\to \widehat {ABM}= \pi - \left( {\widehat {BAM} + \widehat {AMB}} \right) = \dfrac{\pi }{6}\)
=> \(\Delta AMB\) cân tại M
=> UR = UMB = 120V
$ \Rightarrow I = \dfrac{{{U_R}}}{R} = \dfrac{{120}}{{30}} = 4(A)$

