Câu hỏi:
2 năm trước
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, B, C và D. Giữa hai điểm A và B chỉ có tụ điện, giữa hai điểm B và C chỉ có điện trở thuần, giữa 2 điểm C và D chỉ có cuộn cảm thuần cảm. Điện áp hiệu dụng giữa hai điểm A và D là \(100\sqrt 3 V\) và cường độ hiệu dụng chạy qua mạch là \(1{\rm{ }}\left( A \right)\). Điện áp tức thời trên đoạn AC và trên đoạn BD lệch pha nhau \({60^0}\) và giá trị hiệu dụng bằng nhau. Cảm kháng của mạch có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: b
Vẽ lại mạch điện và vẽ giản đồ véctơ, ta được:
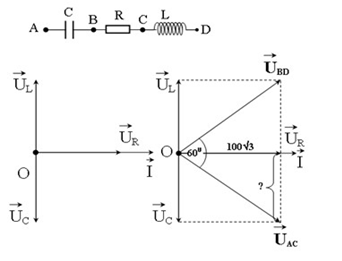
Ta có: \({U_{AC}} = {\rm{ }}{U_{BD}}\) và góc \({U_{BD}}O{U_{AC}}\) bằng \({60^0}\)
=> Tam giác \({U_{BD}}O{U_{AC}}\) là tam giác đều (do tam giác cân có 1 góc = \({60^0}\) là tam giác đều)
Từ giản đồ véctơ, ta có: \({U_L} = {U_C} = \dfrac{{{U_R}}}{{\sqrt 3 }}\) => Mạch cộng hưởng
\(\begin{array}{l} \Rightarrow {U_R} = U = 100\sqrt 3 \,V\\ \Rightarrow {U_L} = \frac{{{U_R}}}{{\sqrt 3 }} = \frac{{100\sqrt 3 }}{{\sqrt 3 }} = 100V\\ \Rightarrow {Z_L} = \frac{{{U_L}}}{I} = 100\Omega \end{array}\)
Hướng dẫn giải:
Sử dụng giản đồ véctơ
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
