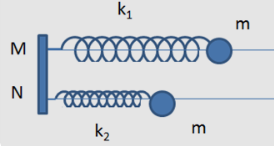
Cho hai con lắc lò xo nằm ngang \((k_1, m)\) và \((k_2, m)\) như hình vẽ. Trục dao động M và N cách nhau \(9cm\). Lò xo \(k_1\) có độ cứng \(100 N/m\); chiều dài tự nhiên \(l_1= 35cm\). Lò xo \(k_2\) có độ cứng \(25N/m\), chiều dài tự nhiên \(l_2= 26cm\). Hai vật có khối lượng cùng bằng \(m\). Thời điểm ban đầu (t = 0), giữ lò xo \(k_1\) dãn một đoạn \(3cm\), lò xo \(k_2\) nén một đoạn \(6cm\) rồi đồng thời thả nhẹ để hai vật dao động điều hoà. Bỏ qua mọi ma sát. Khoảng cách nhỏ nhất giữa hai vật trong quá trình dao động xấp xỉ bằng :
Cách giải :
- Tần số góc của vật 1 và vật 2 là : \(\left\{ \begin{array}{l}{\omega _1} = \sqrt {\dfrac{{{k_1}}}{m}} = \sqrt {\dfrac{{100}}{m}} = \dfrac{{10}}{{\sqrt m }}\\{\omega _2} = \sqrt {\dfrac{{{k_2}}}{m}} = \sqrt {\dfrac{{25}}{m}} = \dfrac{5}{{\sqrt m }}\end{array} \right. \Rightarrow {\omega _1} = 2{\omega _2}\)
- Lò xo k1 có chiều dài tự nhiên l1 = 35cm. Lò xo k2 có chiều dài tự nhiên l2 = 26cm
→ Vị trí cân bằng của hai lò xo cách nhau theo phương ngang 1 đoạn : \(35 – 26 = 9cm\)
- Thời điểm ban đầu (t = 0), giữ lò xo k1 dãn một đoạn 3cm, lò xo k2 nén một đoạn 6cm rồi đồng thời thả nhẹ để hai vật dao động điều hoà. Chọn gốc toạ độ trùng với VTCB của lò xo k1.
→ Phương trình dao động điều hoà của hai vật : \(\left\{ \begin{array}{l}{x_1} = 3\cos \left( {{\omega _1}t} \right) = 3\cos \left( {2.{\omega _2}t} \right)\\{x_2} = - 9 + 6\cos \left( {{\omega _2}t + \pi } \right) = - 9 - 6\cos \left( {{\omega _2}t} \right)\end{array} \right.\)
→ Khoảng cách giữa hai vật theo phương ngang trong quá trình dao động là : \(\Delta x = \left| {{x_1} - {x_2}} \right| = \left| {3\cos \left( {2.{\omega _2}t} \right) + 9 + 6\cos \left( {{\omega _2}t} \right)} \right|\)
Vì :
\(\begin{array}{l}\cos \left( {2.{\omega _2}t} \right) = 2{\cos ^2}\left( {{\omega _2}t} \right) - 1 \Rightarrow \Delta x = \left| {3\left( {2{{\cos }^2}\left( {{\omega _2}t} \right) - 1} \right) + 9 + 6\cos \left( {{\omega _2}t} \right)} \right|\\ \Rightarrow \Delta x = \left| {6.{{\cos }^2}\left( {{\omega _2}t} \right) + 6\cos \left( {{\omega _2}t} \right) + 6} \right|\end{array}\)
Đặt : \(a = \cos \left( {{\omega _2}t} \right) \Rightarrow \Delta x = \left| {6.{a^2} + 6a + 6} \right|\)
Ta có :
\(\begin{array}{l}6.{a^2} + 6a + 6 = 6\left( {{a^2} + a + 1} \right) = 6\left( {{{\left( {a + \dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}} \right) = 6.{\left( {a + \dfrac{1}{2}} \right)^2} + 4,5\\6.{\left( {a + \dfrac{1}{2}} \right)^2} + 4,5 \le 4,5 \Rightarrow {\left( {6.{a^2} + 6a + 6} \right)_{\min }} = 4,5\\ \Rightarrow \Delta {x_{\min }} = 4,5cm\end{array}\)
→ Khoảng cách nhỏ nhất giữa hai vật trong quá trình dao động là : \({d_{\min }} = \sqrt {M{N^2} + \Delta x_{\min }^2} = \sqrt {{9^2} + 4,{5^2}} = 10,06cm\)
Hai dao động điều hoà cùng phương, cùng tần số, cùng pha thì có độ lệch pha bằng
Hai dao động điều hoà cùng phương, cùng tần số, cùng pha thì có độ lệch pha bằng \(\Delta \varphi = 2k\pi \) với \(k = 0,1,\,2...\)
Xét một điểm M bất kì nằm trong miền giao thoa giữa hai sóng được tạo ra bởi hai nguồn kết hợp có cùng phương, cùng tần số, và có biên độ lần lượt là 3 cm và 2 cm. Biên độ dao động của điểm M này không thể nhận giá trị nào sau đây?
Ta có:
\(\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\)
\( \Leftrightarrow \left| {3 - 2} \right| \le A \le 3 + 2\)
\( \Leftrightarrow 1 \le A \le 5\)
Vậy biên độ dao động của điểm M này không thể nhận giá trị là 0,5 cm.
Dao động của một vật có khối lượng 100 g là tổng hợp của hai dao động cùng phương có phương trình lần lượt là \({x_1} = 5\cos \left( {10t + \dfrac{\pi }{3}} \right)\left( {cm} \right);{x_2} = 5\cos \left( {10t - \dfrac{\pi }{6}} \right)\left( {cm} \right)\) (t tính bằng s). Động năng cực đại của vật là
Ta có:
\({x_1} = 5cos\left( {10t + \dfrac{\pi }{3}} \right)cm\)
\({x_2} = 5cos\left( {10t - \dfrac{\pi }{6}} \right)cm\)
Độ lệch pha giữa hai dao động: \(\Delta \varphi = \dfrac{\pi }{3} - \left( { - \dfrac{\pi }{6}} \right) = \dfrac{\pi }{2}rad\)
=> Hai dao động vuông pha nhau
=> Biên độ dao động tổng hợp: \(A = \sqrt {A_1^2 + A_2^2} = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 cm\)
+ Động năng dao động cực đại của vật:
\(\begin{array}{l}{{\rm{W}}_{{d_{max}}}} = {\rm{W}} = \dfrac{1}{2}m{\omega ^2}{A^2}\\ = \dfrac{1}{2}.0,{1.10^2}.\left( {5\sqrt 2 {{.10}^{ - 2}}} \right)\\ = 0,025J = 25mJ\end{array}\)
Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, có đồ thị li độ của các dao động thành phần theo thời gian như hình vẽ. Khi đi qua vị trí cân bằng, vật có tốc độ là
Từ hình vẽ: \(\frac{T}{2} = 0,5s \Rightarrow T = 1\left( s \right)\)
Tần số góc của hai dao động là:
\(\omega = \frac{{2\pi }}{T} = 2\pi \left( {rad/s} \right)\)
Biên độ của hai dao động: \({A_1} = 10cm,\,\,{A_2} = 6\,cm.\)
Lúc \(t = 0,\,\left\{ \begin{array}{l}{x_2} = 6cm = {A_1} \Rightarrow {\varphi _1} = 0\\\left\{ \begin{array}{l}{x_1} = 5cm = \frac{{{A_1}}}{2}\\{v_1} < 0\end{array} \right. \Rightarrow {\varphi _2} = \frac{\pi }{3}\end{array} \right.\)
Phương trình dao động của hai vật là:
\(\left\{ \begin{array}{l}{x_1} = 10\cos \left( {2\pi t + \frac{\pi }{3}} \right)\\{x_2} = 6\cos \left( {2\pi t} \right)\end{array} \right.\)
Biên độ dao động tổng hợp là:
\(\begin{array}{l}A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \left( {\overrightarrow {{A_1}} ,\overrightarrow {{A_2}} } \right)} \\ \Rightarrow A = \sqrt {{{10}^2} + {6^2} + 2.10.6.\cos \frac{\pi }{3}} = 14\left( {cm} \right)\end{array}\)
Khi đi qua vị trí cân bằng, vật có tốc độ là:
\({v_{\max }} = \omega A = 2\pi .14 = 28\pi \)(cm/s)
Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số và có cùng biên độ là 4 cm. Nếu biên độ dao động tổng hợp cũng là 4 cm thì độ lớn độ lệch pha của dao động tổng hợp với dao động thành phần là
Ta có: \({A_2} = {A^2} + A_1^2 - 2A.{A_1}.\cos \left( {\varphi - {\varphi _1}} \right)\)
\(\begin{array}{l} \Leftrightarrow {4^2} = {4^2} + {4^2} - 2.4.4.cos\left( {\varphi - {\varphi _1}} \right)\\ \Leftrightarrow cos\left( {\varphi - {\varphi _1}} \right) = \frac{1}{2} \Rightarrow \left( {\varphi - {\varphi _1}} \right) = \frac{\pi }{3}\end{array}\)
Cho hai dao động điều hoà cùng phương, cùng tần số, cùng biên độ A và lệch pha nhau $\frac{\pi }{3}.$ Dao động tổng hợp của hai dao động này có biên độ là
Biên độ dao động tổng hợp của hai dao động là:
$A=\sqrt{A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}.\cos \left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)}=\sqrt{2{{A}^{2}}+2{{A}^{2}}.\cos \frac{\pi }{3}}=A\sqrt{3}$
Hai dao động điều hòa, cùng phương, cùng tần số, cùng pha, có biên độ lần lượt là A1, A2. Biên độ dao động tổng hợp của hai dao động này là
Vi hai dao động cùng phương và cùng tần số và cùng pha nên biên độ dao động tổng hợp bằng:
A = A1 + A2
Hai dao động vuông pha khi:
Hai dao động vuông pha khi: \(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \)
Hai dao động cùng pha khi:
Hai dao động cùng pha khi: \(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \)
Phát biểu nào sau đây là sai khi nói về độ lệch pha giữa hai dao động:
Ta có:
+ 2 dao động cùng pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \)
+ 2 dao động ngược pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \)
+ 2 dao động vuông pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \)
Biên độ dao động khi 2 dao động vuông pha: \({A^2} = A_1^2 + A_2^2\)
=> Các phương án:
+ A, B, C – đúng
+ D - sai
Hai dao động có phương trình lần lượt là: \({x_1} = 5cos\left( {2\pi t + \frac{\pi }{4}} \right)cm\) và \({x_2} = 10\sin \left( {2\pi t + \frac{\pi }{6}} \right)cm\). Độ lệch pha của hai dao động này có độ lớn bằng:
+ Ta có: \({x_1} = 5cos\left( {2\pi t + \frac{\pi }{4}} \right)cm\)
\({x_2} = 10\sin \left( {2\pi t + \frac{\pi }{6}} \right)cm = 10cos\left( {2\pi t + \frac{\pi }{6} - \frac{\pi }{2}} \right) = 10cos\left( {2\pi t - \frac{\pi }{3}} \right)cm\)
+ Ta có độ lệch pha giữa hai dao động \(\Delta \varphi = \frac{\pi }{4} - \left( { - \frac{\pi }{3}} \right) = \frac{{7\pi }}{{12}}\)
Xét hai dao động điều hòa cùng phương, cùng tần số có phương trình dao động lần lượt là \({x_1} = 4cos\left( {3\pi t - \dfrac{\pi }{3}} \right)cm\),\({x_2} = 2\sin \left( {3\pi t + \dfrac{{5\pi }}{6}} \right)cm\). Pha ban đầu của dao động tổng hợp là:
+ Ta có: \({x_1} = 4cos\left( {3\pi t - \dfrac{\pi }{3}} \right)cm\)
\({x_2} = 2\sin \left( {3\pi t + \dfrac{{5\pi }}{6}} \right)cm = 2cos\left( {3\pi t + \dfrac{{5\pi }}{6} - \dfrac{\pi }{2}} \right) = 2cos\left( {3\pi t + \dfrac{\pi }{3}} \right)cm\)
+ Dao động tổng hợp có pha ban đầu \(\varphi \) được xác định:
\(\begin{array}{l}\tan \varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_2}{\rm{cos}}{\varphi _2}}}\\ = \dfrac{{4.\sin \left( { - \dfrac{\pi }{3}} \right) + 2\sin \left( {\dfrac{\pi }{3}} \right)}}{{4.c{\rm{os}}\left( { - \dfrac{\pi }{3}} \right) + 2c{\rm{os}}\left( {\dfrac{\pi }{3}} \right)}} = - \dfrac{\sqrt{3}}{3}\\ \to \varphi = - {30^0}\end{array}\)
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số có phương trình lần lượt là: \({x_1} = {\rm{ }}{A_1}cos\left( {\omega t + {\varphi _1}} \right)\) và \({x_2} = {\rm{ }}{A_2}cos\left( {\omega t + {\varphi _2}} \right)\). Biên độ dao động A của vật được xác định bởi công thức nào sau đây?
Biên độ dao động tổng hợp A được xác định bởi biểu thức:
\(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos ({\varphi _2} - {\varphi _1})} \)
Cho hai dao động điều hòa cùng phương, cùng tần số, lệch pha nhau một góc \(4\pi \) với biên độ dao động \({A_1}\) và \({A_2}\). Dao động tổng hợp của hai dao động trên có biên độ là:
Ta có, độ lệch pha của hai dao động \(4\pi \) (hai dao động cùng pha nhau)
=> Biên độ dao động tổng hợp của hai dao động: \(A = {A_1} + {A_2}\)
Cho hai dao động điều hòa cùng phương, cùng tần số, lệch pha nhau một góc \(5\pi \) với biên độ dao động \({A_1}\) và \({A_2}\). Dao động tổng hợp của hai dao động trên có biên độ là:
Ta có, độ lệch pha của hai dao động \(5\pi \) (hai dao động ngược pha nhau)
=> Biên độ dao động tổng hợp của hai dao động: \(A = \left| {{A_1} - {A_2}} \right|\)
Phát biểu nào sau đây là đúng khi nói về biên độ của dao động tổng hợp của hai dao động điều hoà cùng phương cùng tần số?
+ A – sai vì: Biên độ của dao động tổng hợp \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}cos\Delta \varphi } \) không phụ thuộc vào tần số của hai dao động thành phần
+ B – sai vì: Biên độ của dao động tổng hợp phụ thuộc vào độ lệch pha \(\Delta \varphi \) của hai dao động thành phần
+ C – sai vì: Biên độ của dao động tổng hợp lớn nhất khi hai dao động thành phần cùng pha: \(A = {A_1} + {A_2}\)
+ D – đúng vì khi đó, biên độ dao động tổng hợp: \(A = \left| {{A_1} - {A_2}} \right|\)
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, có các phương trình dao động thành phần lần lượt là: \({x_1} = 8cos\left( {20t + \frac{\pi }{6}} \right)cm\) và \({x_2} = 3cos\left( {20t + \frac{{5\pi }}{6}} \right)cm\). Biên độ dao động của vật là:
+ Độ lệch pha giữa hai dao động: \(\Delta \varphi = \frac{{5\pi }}{6} - \frac{\pi }{6} = \frac{{2\pi }}{3}\)
+ Biên độ dao động tổng hợp của hai dao động thành phần:
\(\begin{array}{l}A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}cos\Delta \varphi } \\ = \sqrt {{8^2} + {3^2} + 2.8.3.cos\frac{{2\pi }}{3}} \\ = 7cm\end{array}\)
Một vật thực hiện đồng thời hai dao động điều hoà cùng phương cùng tần số có biên độ lần lượt là \({A_1} = 7cm\) và \({A_2} = 9cm\). Biên độ dao động tổng hợp \(A\) của vật không thể có giá trị nào sau đây?
Biên độ dao động tổng hợp thỏa mãn điều kiện:
\(\begin{array}{l}|{A_1} - {A_2}| \le A \le {A_1} + {A_2}\\ \to \left| {9 - 7} \right| \le A \le 9 + 7\\ \to 2 \le A \le 16\end{array}\)
=> Biên độ dao động tổng hợp A của vật không thể là \(18cm\)
Hai dao động thành phần có biên độ là \(6cm\) và \(8cm\). Biên độ dao động tổng hợp có thể nhận giá trị:
Biên độ dao động tổng hợp thỏa mãn điều kiện
\(\begin{array}{l}\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\\ \leftrightarrow \left| {8 - 6} \right| \le A \le 8 + 6\\ \leftrightarrow 2 \le A \le 14\end{array}\)
Vậy chỉ có \(A = 3cm\) thỏa mãn điều kiện trên

