Mẫu nguyên tử Bo - Quang phổ của nguyên tử Hidro

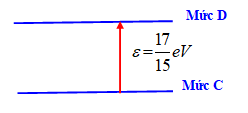
Để electron chuyển từ trạng thái có mức năng lượng C lên trạng thái có mức năng lượng D thì cần nhận photon có năng lượng:

 $\varepsilon  = {E_D} - {E_C} \\\to \dfrac{{17}}{{15}} = \left( {\dfrac{{ - 13,6}}{{n_D^2}} + \dfrac{{13,6}}{{n_C^2}}} \right)\\ \to \dfrac{1}{{n_C^2}} - \dfrac{1}{{n_D^2}} = \dfrac{1}{{13}} \\\to \dfrac{1}{{n_C^2}} > \dfrac{1}{{12}} \\\to {n_C} < 3,5$

+ n_C=1$\to \dfrac{1}{{n_C^2}} = 1$(loại)

+ n_C=2$\to \dfrac{1}{{n_C^2}} = \dfrac{1}{4}$(loại)

+ n_C=3$\to \dfrac{1}{{n_C^2}} = \dfrac{1}{9} \to {n_D} = 6$

Bán kính quỹ đạo nguyên tử hiđrô đã tăng thêm: $\Delta r = {6^2}{r_o} - {3^2}{r_o} = 27{r_o}$

Các mức năng lượng ${E_1},\,\,{E_2},\,\,{E_3}$ tương ứng với các trạng thái dừng trên các quỹ đạo $K,\,\,L,\,\,M.$

Vậy khi nguyên tử hiđrô hấp thụ một phôtôn có năng lượng $\varepsilon  = {E_3} - {E_1}$ thì êlectron chuyển từ quỹ đạo $K$ lên quỹ đạo $M.$

Khi nguyên tử chuyển từ trạng thái dừng có năng lượng −3,4 eV sang trạng thái dừng có năng lượng −13,6 eV thì nó phát ra một phôtôn có năng lượng là $\varepsilon  =  - 3,4 - ( - 13,6) = 10,2eV$

Ta có: $\left\{ \begin{array}{l}{\varepsilon _1} = \frac{{hc}}{{{\lambda _1}}} = {E_L} - {E_K}\\{\varepsilon _2} = \frac{{hc}}{{{\lambda _2}}} = {E_M} - {E_L}\end{array} \right.$  

Khi electron chuyển từ quỹ đạo M về quỹ đạo K:

${\varepsilon _3} = \frac{{hc}}{{{\lambda _3}}} = {E_M} - {E_K} = {E_M} - {E_L} + {E_L} - {E_K} = {\varepsilon _2} + {\varepsilon _1}$

$\Leftrightarrow \frac{{hc}}{{{\lambda _3}}} = \frac{{hc}}{{{\lambda _1}}} + \frac{{hc}}{{{\lambda _2}}} \Rightarrow {\lambda _3} = \frac{{{\lambda _1}.{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}} = 102,734nm$

Mẫu Bohr đưa ra khái niệm trạng thái dừng là trạng thái có năng lượng xác định, còn mẫu Rutherford thì không có khái niệm trạng thái dừng.

Công thức tính lực hướng tâm: ${F_{ht}} = \frac{{m{v^2}}}{r}$

Biểu thức của định luật Culong: $F = \frac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}$

Khi electron chuyển động trên quỹ đạo dừng thì lực hút tĩnh điện đóng vai trò lực hướng tâm.

Ta có:  $k\frac{{\left| {{q_1}{q_2}} \right|}}{{r_n^2}} = \frac{{m{v^2}}}{{{r_n}}} \Rightarrow {v_n} = \sqrt {k.\frac{{\left| {{q_1}{q_2}} \right|}}{{m.{r_n}}}}$

$\Rightarrow \frac{{{v_K}}}{{{v_M}}} = \sqrt {\frac{{k.\frac{{\left| {{q_1}{q_2}} \right|}}{{m.{r_K}}}}}{{k.\frac{{\left| {{q_1}{q_2}} \right|}}{{m.{r_M}}}}}}  = \sqrt {\frac{{{r_M}}}{{{r_K}}}}$

Mặt khác bán kính quỹ đạo dừng được xác định là ${r_n} = {\rm{ }}{n^2}.{r_0}$

Quỹ đạo K ứng với $n = 1$; quỹ đạo M ứng với $n = 3$

Nên tỉ số $\frac{{{v_L}}}{{{v_N}}} = \frac{{\sqrt {{3^2}.{r_0}} }}{{\sqrt {{1^2}.{r_0}} }} = 3$

+ Khi chiếu bức xạ có tần số f₁ vào đám nguyên tử này thì chúng phát ra tối đa 3 bức xạ:

${N_1} = \dfrac{{{n_1}\left( {{n_1} - 1} \right)}}{2} = 3 \Rightarrow {n_1} = 3$

$\Rightarrow h{f_1} =  - \dfrac{{{E_0}}}{{{3^2}}} - \left( { - \dfrac{{{E_0}}}{{{1^2}}}} \right) = \dfrac{8}{9}{E_0}$

+ Lại có:

$\begin{array}{l}h{f_2} = 1,08.h{f_1} =  - \dfrac{{{E_0}}}{{n_2^2}} - \left( { - \dfrac{{{E_0}}}{{{1^2}}}} \right)\\ \Leftrightarrow 1.08.\dfrac{8}{9}{E_0} =  - \dfrac{{{E_0}}}{{n_2^2}} + {E_0} \Rightarrow {n_2} = 5\end{array}$

Số bức xạ phát ra tối đa:

${N_2} = \dfrac{{{n_2}\left( {{n_2} - 1} \right)}}{2} = \dfrac{{5.\left( {5 - 1} \right)}}{2} = 10$

Khi electron chuyển động tròn đều quanh hạt nhân, lực Cu – lông đóng vai trò là lực hướng tâm

Ta có: ${F_C} = {F_{ht}} \Rightarrow k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = \dfrac{{m{v^2}}}{r} \Rightarrow k\dfrac{{{e^2}}}{{{r^2}}} = m{\omega ^2}r$

$\begin{array}{l} \Rightarrow \omega  = \sqrt {\dfrac{{k{e^2}}}{{m{r^3}}}}  = \sqrt {\dfrac{{k{e^2}}}{{m{{\left( {{n^2}{r_0}} \right)}^3}}}}  = \sqrt {\dfrac{{k{e^2}}}{{m{{\left( {{2^2}{r_0}} \right)}^3}}}} \\ \Rightarrow \omega  = \sqrt {\dfrac{{{{9.10}^9}.{{\left( {1,{{6.10}^{ - 19}}} \right)}^2}}}{{9,{{1.10}^{ - 31}}.{{\left( {{2^2}.5,{{3.10}^{ - 11}}} \right)}^3}}}}  = 5,{15.10^{15}} = 0,{5.10^{16}}\,\,\left( {rad/s} \right)\end{array}$

Khi hạt nhân Hidro chuyển từ mức năng lượng E_m sang mức năng lượng E_n thì nó phát ra (hoặc hấp thụ) một photon có năng lượng :

$\begin{array}{l} \varepsilon = \frac{{hc}}{\lambda } = {E_n} - {E_m} = ( - 0,85) - ( - 3,40) = 2,55eV = 4,{08.10^{ - 19}}J\\ \Rightarrow \lambda = \frac{{hc}}{\varepsilon } = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{4,{{08.10}^{ - 19}}}} = 0,{48.10^{ - 6}}m = 0,48\mu m \end{array}$

Ta có: ${E_n} - {E_m} = hf = \dfrac{{hc}}{\lambda }$

$\begin{array}{l} \Rightarrow {E_n} = \dfrac{{hc}}{{\lambda .1,{{6.10}^{ - 19}}}} - 13,6(eV)\\ = \dfrac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{0,{{1218.10}^{ - 6}}.1,{{6.10}^{ - 19}}}} - 13,6\\ =  - 3,4eV\end{array}$

Khi bán kính quỹ đạo là, 132,5.10^-11m, ${{n}_{1}}=\sqrt{\frac{{{r}_{n}}}{{{r}_{O}}}}=5$

Lực Culong giữa electron và hạt nhân có vai trò là lực hướng tâm: ${{F}_{ht}}=k\frac{{{e}^{2}}}{{{r}_{n}}}={{m}_{e}}\frac{{{v}^{2}}}{r}\to v=e.\sqrt{\frac{k}{{{m}_{e}}.{{r}_{n}}}}=\frac{{{2,2.10}^{6}}}{n}$=> v tỉ lệ nghịch với n

Quãng đường electron đi được trong một khoảng thời gian tỉ lệ thuận với vận tốc chuyển  động của electron, nên tỉ lệ nghịch với n.

$\to \frac{{{S}_{1}}}{{{S}_{2}}}=\frac{{{n}_{2}}}{{{n}_{1}}}\to {{S}_{2}}=\frac{{{S}_{1}}{{n}_{1}}}{{{n}_{2}}}=\frac{3S.5}{3}=5S$

Chọn C

Áp dụng tiên đề về trạng thái dừng của nguyên tử trong mẫu nguyên tử Bo

Quỹ đạo dừng M có $n =3$

$\to r=n^2r_0=3^2.5,3.10^{-11}=4,77.10^{-10}m$

Bán kính quỹ đạo Bo: ${r_n} = {n^2}{r_0}$

Quỹ đạo dừng N ứng với $n = 4$

$\Rightarrow {r_N} = {4^2}{r_0} = 16{r_0}$

Quỹ đạo $L$ ứng với $n = 2;$ quỹ đạo $N$ ứng với $n = 4.$

Ta có: $\dfrac{{{r_N}}}{{{r_L}}} = \dfrac{{{4^2}{r_0}}}{{{2^2}{r_0}}} = 4 \Rightarrow {r_N} = 4{r_L}$

Ta có:

$\dfrac{{hc}}{\lambda } = {E_1} - {E_2} \\\to \lambda  = \dfrac{{hc}}{{{E_1} - {E_2}}} = \dfrac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{( - 0,544 + 3,4).1,{{6.10}^{ - 19}}}} \approx 0,{4349396.10^{ - 6}}(m)$

Quỹ đạo O có n = 5; quỹ đạo M có n = 3

Bán kính quỹ đạo dừng M và O là:${r_M} = {{{r_0}}}{{{3^2}}} = {{{r_0}}}{9};{r_O} = {{{r_0}}}{{{5^2}}} = {{{r_0}}}{{25}}$

Vậy khi chuyển từ quỹ đạo O về M thì bán kính quỹ đạo giảm: 25r₀ - 9r₀ = 16r₀

Electron chuyển động tròn trong nguyên tử hidro nên lực điện đóng vai trò lực hướng tâm

$k\dfrac{{{e^2}}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} \\\Rightarrow {v^2} = \dfrac{{k{e^2}}}{{mr}} = \dfrac{{k{e^2}.{n^2}}}{{m{r_0}}}$

Để tốc độ giảm 3 lần thì n tăng lên 3 lần vậy electron chuyển động trên quỹ đạo M có $n = 3$

Theo mẫu nguyên tử Bo, trạng thái dừng của nguyên tử có thể là trạng thái cơ bản hoặc trạng thái kích thích.

Theo mẫu nguyên tử Bo, bán kính quỹ đạo dừng được xác định bởi:

${r_n} = {n^2}{r_0}$

Bán kính của quỹ đạo Bo thứ 5 là :

${r_5} = {5^2}.{r_0} = 25.0,{53.10^{ - 10}} = 13,{25.10^{ - 10}}m$