Mẫu nguyên tử Bo - Quang phổ của nguyên tử Hidro

Quỹ đạo dừng có bán kính  r_n = 13,25.10^-10 m = 5²r₀   => n = 5  =>  Quỹ đạo O

Theo bài ra ta có:

\(\begin{array}{l}{r_m} = {m^2}{r_0}\left( {m \in {N^*}} \right);{r_n} = {n^2}{r_0}\left( {n \in {N^*}} \right)\\ \Rightarrow {r_m} - {r_n} = 36{r_0} \Rightarrow {m^2} - {n^2} = 36 \Rightarrow \left( {m - n} \right)\left( {m + n} \right) = 36\end{array}\)

 m – n và m + n là ước của 36. Mặt khác tổng của m – n và m + n là một số chẵn nên hai số m – n và m + n sẽ cùng chẵn hoặc cùng lẻ

\( \Rightarrow \left\{ \begin{array}{l}m - n = 2\\m + n = 18\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m = 10\\n = 8\end{array} \right. \Rightarrow {r_m} = 100{r_0}\)

Nguyên tử Hiđrô đang ở trạng thái dừng có mức năng lượng cơ bản thì hấp thụ một photon có năng lượng \(\varepsilon  = {\rm{ }}{E_N}-{\rm{ }}{E_K}\)  .

Khi đó nguyên tử sẽ chuyển thẳng từ K lên N

\({F_c} = {F_{ht}} \Leftrightarrow \dfrac{{k{e^2}}}{{r_n^2}} = \dfrac{{mv_n^2}}{{{r_n}}} \Rightarrow {v_n} = \sqrt {\dfrac{{k{e^2}}}{{m{r_n}}}} \)

Quỹ đạo K ứng với \(n = 1\)

Ta suy ra tốc độ của electron chuyển động trên quỹ đạo K là: \({v_K} = \sqrt {\dfrac{{{{9.10}^9}.{{\left( {1,{{6.10}^{ - 19}}} \right)}^2}}}{{9,{{1.10}^{ - 31}}.5,{{3.10}^{ - 11}}}}}  = 2,{19.10^6}m/s\)

\({F_{ht}} = \dfrac{{k{e^2}}}{{r_n^2}} = \dfrac{{mv_n^2}}{{{r_n}}} \\\Rightarrow v_n^2 = \dfrac{{k{e^2}}}{{m{r_n}}} = \dfrac{{k{e^2}}}{{m.{n^2}{r_0}}}\)

Lại có:

\({v_n} = {\omega _n}{r_n} = {\omega _n}{n^2}{r_0} \\\Rightarrow {\omega _n} = \dfrac{1}{{{n^3}}}\sqrt {\dfrac{{k{e^2}}}{{mr_0^3}}} \\ \Rightarrow \dfrac{{{\omega _O}}}{{{\omega _M}}} = {\left( {\dfrac{{{n_M}}}{{{n_O}}}} \right)^3} = {\left( {\dfrac{3}{5}} \right)^3} = \dfrac{{27}}{{125}}\)

Theo đề bài ta có:

\(\begin{array}{l}{r_n} + {r_{n + 7}} = {r_{n + 8}}\\ \Leftrightarrow {n^2}{r_0} + {(n + 7)^2}{r_0} = {(n + 8)^2}{r_0}\\ \Leftrightarrow {n^2} + {\left( {n + 7} \right)^2} = {\left( {n + 8} \right)^2}\\ \Leftrightarrow {n^2} - 2n - 15 = 0\\ \Rightarrow \left[ \begin{array}{l}n = 5\\n =  - 3\left( {loai} \right)\end{array} \right.\end{array}\)

Khi đó lực tương tác giữa electron và hạt nhân trong nguyên tử hidro ở quỹ đạo dừng n là :

\(F = \dfrac{{k{e^2}}}{{{r^2}}} = \dfrac{{{{9.10}^9}.{{(1,{{6.10}^{ - 19}})}^2}}}{{{{(25.5,{{3.10}^{ - 11}})}^2}}} = 1,{3.10^{ - 10}}N\)

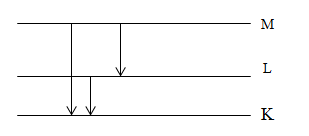
Ba bức xạ ứng với: M về K, L về K, M về L

Ta có \(I = \dfrac{q}{t} = \dfrac{q}{T}\xrightarrow{{v = \omega r \Rightarrow T = \dfrac{{2\pi r}}{v}}}I = \dfrac{{|e|v}}{{2\pi r}}\)

Lại có : \(F = k\dfrac{{{e^2}}}{{{r^2}}} = m\dfrac{{{v^2}}}{r} =  > v = \sqrt {k\dfrac{{{e^2}}}{{m.r}}} \xrightarrow{{\left( 1 \right)}}I = \dfrac{{|e|\sqrt {k\dfrac{{{e^2}}}{{m.{r^3}}}} }}{{2\pi }} =  > \dfrac{{{I_1}}}{{{I_2}}} = \sqrt {{{\left( {\dfrac{{{r_2}}}{{{r_1}}}} \right)}^3}} \)

Khi ở L thì \(n{\text{ }} = {\text{ }}2{\text{ }} =  > {\text{ }}{r_1} = {\text{ }}{2^2}.{r_0}\)

Khi ở N thì \(n{\text{ }} = {\text{ }}4{\text{ }}= > {\text{ }}{r_2} = {\text{ }}{4^2}.{r_0}\)

=  > \(\dfrac{{{I_1}}}{{{I_2}}} = \sqrt {{{\left( {\dfrac{{{4^2}}}{{{2^2}}}} \right)}^3}}  = 8\)

Ta suy ra: \(\dfrac{I_2}{I_1}=\dfrac{1}{8}\)

Ta có:

\(\Delta E = \frac{{hc}}{\lambda } =  - 0,85 - \left( { - 13,6} \right) = 12,75eV \Rightarrow \lambda  = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{12,75.1,{{6.10}^{ - 19}}}} = 0,0974\mu m\)

Ta có :

 \({E_{M\;}} - \;{E_{L\;}} = \frac{{hc}}{\lambda } = {\rm{ }}1,9.1,{6.10^{ - 19}}J \Rightarrow \lambda  = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{1,9.1,{{6.10}^{ - 19}}}} = \;0,654{\rm{ }}\mu m\)

Ta có :

\({E_3} - {E_1} = h{f_{31}};{E_2} - {E_1} = h{f_{21}} \Rightarrow {E_3} - {E_2} = h{f_{32\;}} = \;h{f_{31\;}} - \;h{f_{21}} \Rightarrow \;{f_{32}}\; = {\rm{ }}{f_{31}}\;-{\rm{ }}{f_{21}}\)

Ta có:

\({E_{32}} = {E_3} - {E_2} = \left( {{E_3} - {E_1}} \right) - \left( {{E_2} - {E_1}} \right) \Leftrightarrow \frac{{hc}}{{{\lambda _{32}}}} = \frac{{hc}}{{{\lambda _{31}}}} - \frac{{hc}}{{{\lambda _{21}}}} \Leftrightarrow \frac{1}{{{\lambda _{32}}}} = \frac{1}{{{\lambda _{32}}}} - \frac{1}{{{\lambda _{21}}}} \Rightarrow {\lambda _{32}} = \frac{{{\lambda _{21}}.{\lambda _{32}}}}{{{\lambda _{21}} - {\lambda _{32}}}}\)

Bước sóng vạch quang phổ thứ nhất của dãy Banme:

\({\lambda _{32}} = {\rm{ }}0,656\mu m\)

Bước sóng vạch quang phổ thứ hai của dãy Banme:

\({\lambda _{42}} = {\rm{ }}0,486\mu m\)

Bước sóng vạch đầu tiên trong trong dãy Pasen:

\({\lambda _{43}}\)  

Áp dụng tiên đề Bo:

\(\begin{array}{l}{E_{43}} = {E_4} - {E_3} = {E_4} - {E_2} + {E_2} - {E_3} = \left( {{E_4} - {E_2}} \right) - \left( {{E_3} - {E_2}} \right)\\ \Leftrightarrow \frac{{hc}}{{{\lambda _{43}}}} = \frac{{hc}}{{{\lambda _{42}}}} - \frac{{hc}}{{{\lambda _{32}}}} \Leftrightarrow \frac{1}{{{\lambda _{43}}}} = \frac{1}{{{\lambda _{42}}}} - \frac{1}{{{\lambda _{32}}}} \Rightarrow {\lambda _{43}} = 1,8754\mu m\end{array}\)

Khi chuyển từ quỹ đạo M về quỹ đạo L, nguyên tử hidrô phát ra phôtôn có bước sóng:

\({\lambda _{32}} = {\rm{ }}0,6563\mu m\)

Khi chuyển từ quỹ đạo N về quỹ đạo L, nguyên tử hidro phát ra phôtôn có bước sóng :

\({\lambda _{42}} = {\rm{ }}0,4861{\rm{ }}\mu m\)

Khi chuyển từ quỹ đạo N về quỹ đạo M, nguyên tử hidro phát ra phôtôn có bước sóng:

\({\lambda _{43}}\)

Ta có:

\({E_{43}} = {E_4} - {E_3} = \left( {{E_4} - {E_2}} \right) - \left( {{E_3} - {E_2}} \right) \Leftrightarrow \frac{{hc}}{{{\lambda _{43}}}} = \frac{{hc}}{{{\lambda _{42}}}} - \frac{{hc}}{{{\lambda _{32}}}} \Leftrightarrow \frac{1}{{{\lambda _{43}}}} = \frac{1}{{{\lambda _{42}}}} - \frac{1}{{{\lambda _{32}}}} \Rightarrow {\lambda _{43}} = \frac{{{\lambda _{32}}{\lambda _{42}}}}{{{\lambda _{32}} - {\lambda _{42}}}} = 1,8744\mu m\)

Khi e chuyển từ quỹ đạo L về quỹ đạo K thì phát phát ra photon có năng lượng:

\(\Delta E = \left( { - \frac{1}{{{2^2}}} - \left( { - \frac{1}{{{1^2}}}} \right)} \right){E_0} = \frac{{3{E_0}}}{4}\left( {eV} \right) = \frac{{hc}}{\lambda }(1)\)

Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo dừng thứ n + 1 sang quỹ đạo dừng thứ n:

\(\Delta E' = \frac{{5{E_0}}}{{36}} = \frac{{hc}}{{{\lambda _0}}}(2)\)

(1) : (2) ta được:

\(\lambda  = \frac{5}{{27}}{\lambda _0}\)

Từ giản đồ năng lượng của Hiđrô ta có:

 \({f_1} = {\rm{ }}{f_{\infty 2}};{\rm{ }}{f_2} = {\rm{ }}{f_{32}};{\rm{ }}{f_3} = {\rm{ }}{f_{\infty 3}}\)

Áp dụng tiên đề Bo:

 \(\begin{array}{l}h{f_\infty }_3 = {\rm{ }}{E_\infty } - {\rm{ }}{E_3} = {\rm{ }}{E_\infty } - {\rm{ }}{E_2} + {\rm{ }}{E_2} - {\rm{ }}{E_3}\;\\ \Leftrightarrow h{f_\infty }_3 = h{f_\infty }_2 + h{f_{23}} \\\Leftrightarrow {f_\infty }_3 = {f_\infty }_2 + {f_{23}} = {f_\infty }_2 - {f_{32}} \\\Leftrightarrow {f_3} = {f_1} - {f_2} \\\Leftrightarrow {f_1} = {f_2} + {f_3}\end{array}\)

Bước sóng của vạch H:

\({\lambda _{32}} = {\rm{ }}{\lambda _1} = 656nm\)

Bước sóng của vạch H:

\({\lambda _{42}} = {\rm{ }}{\lambda _2} = 486nm\)

Bước sóng của vạch quang phổ đầu tiên trong dãy Pasen:

\({\lambda _{43}}\)

\(\frac{1}{{{\lambda _{43}}}} = \frac{1}{{{\lambda _{42}}}} - \frac{1}{{{\lambda _{32}}}} = \frac{1}{{{\lambda _2}}} - \frac{1}{{{\lambda _1}}} \Rightarrow {\lambda _{43}} = \frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} - {\lambda _2}}} = 1875,4nm = 1,8754\mu m\)

Ta có:

\(\Delta E = \frac{{hc}}{\lambda } \to \lambda \)lớn nhất khi E nhỏ nhất, \(\lambda \)  nhỏ nhất khi \(\Delta E\) lớn nhất

Bước sóng dài nhất của dãy Laiman là:

\({\lambda _{21}} = \;0,1216\mu m\)

Bước sóng ngắn nhất của dãy Banme là:

\({\lambda _{\infty 2}}\; = 0,3650{\rm{ }}\mu m\)

Bước sóng ngắn nhất của bức xạ mà hiđrô có thể phát ra:

\({\lambda _{\infty 1}}\)

\(\frac{1}{{{\lambda _{\infty 1}}}} = \frac{1}{{{\lambda _{\infty 2}}}} + \frac{1}{{{\lambda _{21}}}} \Rightarrow {\lambda _{\infty 1}} = \frac{{{\lambda _{\infty 2}}{\lambda _{21}}}}{{{\lambda _{\infty 2}} + {\lambda _{21}}}} = 0,0912\mu m\)

Do nguyên tử có thể phát ra tối đa 15 bức xạ   n.(n – 1)/2 = 15  n = 6

Ta có:

\(\Delta E = \frac{{hc}}{\lambda } \to \lambda \)lớn nhất khi E nhỏ nhất, \(\lambda \) nhỏ nhất khi E lớn nhất

Bước sóng dài nhất:

\({\lambda _{max}} = {\lambda _{65}}\)

Bước sóng nhỏ nhất:

\({\lambda _{min}} = {\lambda _{61}}\)

\(\left\{ \begin{array}{l}\frac{{hc}}{{{\lambda _{m{\rm{ax}}}}}} = \frac{{hc}}{{{\lambda _{65}}}} = {E_6} - {E_5} = A\left( {\frac{1}{{25}} - \frac{1}{{36}}} \right)\\\frac{{hc}}{{{\lambda _{\min }}}} = \frac{{hc}}{{{\lambda _{61}}}} = {E_6} - {E_1} = A\left( {1 - \frac{1}{{36}}} \right)\end{array} \right. \Rightarrow \frac{{{\lambda _{m{\rm{ax}}}}}}{{{\lambda _{\min }}}} = 79,5\)

Ta có: Khi nguyên tử chuyển từ trạng thái dừng có năng lượng E_n sang trạng thái có năng lượng E_m < E_n thì nó phát ra một photon có năng lượng $\varepsilon  = {E_n} - {E_m}$.