Chất phóng xạ pôlôni phát ra tia \(\alpha\) và biến đổi thành chì . Gọi chu kì bán rã của pôlôni là \(T\). Ban đầu \((t = 0)\) có một mẫu nguyên chất. Trong khoảng thời gian từ \(t = 0\) đến \(t = 2T\), có \(63 mg\) trong mẫu bị phân rã. Lấy khối lượng nguyên tử tính theo đơn vị \(u\) bằng số khối của hạt nhân của nguyên tử đó. Trong khoảng thời gian từ \(t = 2T \) đến \(t = 3T\), lượng chì được tạo thành trong mẫu có khối lượng là:
\({m_o} - \dfrac{{{m_o}}}{{{2^2}}} = 63mg \to {m_o} = 84mg\)
+ Thời điểm \(t=2T\) ta có: \({m_o}^\prime = \dfrac{{{m_o}}}{4} = 21mg\)
+ Số hạt Po bị phân rã trong thời gian từ \(2T\) đến \(3T\) là:
\(\begin{array}{l}\Delta N = \dfrac{{{m_0}'}}{{2.210}}.{N_A}\\ \to {m_{Pb}} = \dfrac{{\Delta N}}{{{N_A}}}{A_{Pb}} = \dfrac{{\dfrac{{{m_0}'}}{{2.210}}.{N_A}}}{{{N_A}}}.{A_{Pb}}\\ = \dfrac{{21}}{{2.210}}.206 = \dfrac{{103}}{{10}} = 10,3mg\end{array}\)
Dùng hạt \(\alpha\) có động năng \(5,50 MeV\) bắn vào hạt nhân \(_{13}^{27}Al\) đứng yên gây ra phản ứng: \(_2^4He + _{13}^{27}Al \to X + _0^1n\). Phản ứng này thu năng lượng \(2,64 MeV\) và không kèm theo bức xạ gamma. Lấy khối lượng các hạt nhân tính theo đơn vị \(u\) bằng số khối của chúng. Khi hạt nhân \(X\) bay ra theo hướng lệch với hướng chuyển động của hạt một góc lớn nhất thì động năng của hạt nơtron \(\alpha\) gần nhất với giá trị nào sau đây?
Ta có \({K_X} + {K_n} = 5,5 - 2,64 = 2,86 \to {K_n} = 2,86 - {K_X}\)
Vẽ giản đồ véc tơ \(\overrightarrow {{P_\alpha }} {\rm{}} = \overrightarrow {{P_X}} {\rm{}} + \overrightarrow {{P_n}} \);
Gọi \(\beta \) là góc hợp bởi hướng lệch của hạt X so với hướng chuyển động của hạt α ta có :
\(\begin{array}{l}cos\beta = \dfrac{{p_X^2 + p_\alpha ^2 - p_H^2}}{{2{p_X}{p_\alpha }}} = \dfrac{{30{K_X} + 22 - 2,86 + {K_X}}}{{4\sqrt {120} \sqrt {{K_X}} }}\\ = \dfrac{{31\sqrt {{K_X}} + \dfrac{{19,14}}{{\sqrt {{K_X}} }}}}{{4\sqrt {120} }}\end{array}\)
Ta có: \(31\sqrt {{K_X}} + \dfrac{{19,14}}{{\sqrt {{K_X}} }} \ge 2\sqrt {31\sqrt {{K_X}} .\dfrac{{19,14}}{{\sqrt {{K_X}} }}} \approx 48,72\)
=> Để \(\beta \) đạt giá trị lớn nhất khi: \(31\sqrt {{K_X}} = \dfrac{{19,14}}{{\sqrt {{K_X}} }} \to {K_X} = 0,6174MeV\)
=> \({K_n} = 2,86 - {K_X} = 2,86 - 0,6174 = 2,243MeV\)
Rađi \(_{88}^{226}Ra\) là nguyên tố phóng xạ \(\alpha \). Một hạt nhân \(_{88}^{226}Ra\) đang đứng yên phóng ra hạt \(\alpha \) và biến đổi thành hạt nhân con X. Biết động năng của hạt \(\alpha \) là \(4,8{\rm{ }}MeV\). Lấy khối lượng hạt nhân (tính theo đơn vị u) bằng số khối của nó. Giả sử phóng xạ này không kèm theo bức xạ gamma. Năng lượng tỏa ra trong phân rã này là:
+ Phương trình phản ứng \(_{88}^{226}Ra \to _2^4He + _{86}^{224}X\)
+ Áp dụng định luật bảo toàn năng lượng toàn phần và định luật bảo toàn động lượng ta có
\(\begin{array}{l}\left\{ \begin{array}{l}\Delta E = {K_{He}} + {K_X}\\{p_{He}} = {p_x} \Leftrightarrow p_{He}^2 + p_X^2\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\Delta E = {K_{He}} + {K_X}\\{m_{He}}{K_{He}} = {m_X}{K_X}\end{array} \right.\\ = > \Delta E = {K_{He}} + \dfrac{{{m_{He}}{K_{He}}}}{{{m_X}}}\\ = > \Delta E = 4,8 + \dfrac{4}{{226}}.4,8 \approx 4,89MeV\end{array}\)
Chất phóng xạ pôlôni \(_{84}^{210}Po\) phát ra tia \(\alpha\) và biến đổi thành chì. Cho chu kì bán rã cùa pôlôni là \(138\) ngày. Ban đầu có một mẫu pôlôni nguyên chất, sau khoảng thời gian \(t\) thì tỉ số giữa khối lượng chì sinh ra và khối lượng pôlôni còn lại trong mẫu là \(0,6\). Coi khối lượng nguyên từ bằng số khối của hạt nhân của nguyên tử đó tính theo đơn vị \(u\). Giá trị của \(t\) là:
Phương trình phản ứng: \(_{84}^{210}Po \to _2^4He + _{82}^{206}Pb\)
\(\dfrac{{{m_{Pb}}}}{{{m_{Po}}}} = \dfrac{{{A_{Pb}}\Delta N}}{{{A_{Po}}\Delta N}} = \dfrac{{{A_{Pb}}{N_0}\left( {1 - {2^{\dfrac{{ - t}}{T}}}} \right)}}{{{A_{Po}}{N_0}{2^{\dfrac{{ - t}}{T}}}}} = \dfrac{{206.\left( {1 - {2^{\dfrac{{ - t}}{{138}}}}} \right)}}{{{{210.2}^{\dfrac{{ - t}}{{238}}}}}} = 0,6\)
\( \Rightarrow t \approx 95,15\) ngày
Cho phản ứng hạt nhân: \({}_3^7Li + _1^1H \to _2^4He + X\) . Năng lượng tỏa ra khi tổng hợp được 1 mol heli theo phản ứng này là \(5,{2.10^{24}}MeV\). Lấy \({N_A} = {\rm{ }}6,{02.10^{23}}mo{l^{ - 1}}\). Năng lượng tỏa ra của một phản ứng hạt nhân trên là:
Phương trình phản ứng : \(_3^7Li + _1^1H \to _2^4He + _2^4He\)
Từ phương trình phản ứng => X cũng là hạt nhân Heli
=> Mỗi phản ứng trên cho 2 hạt He vậy 1 mol He chứa \(N = n{N_A} = {1.6,02.10^{23}}\) hạt nhân He
Khi tổng hợp \({6,02.10^{23}}\) hạt nhân He năng lượng tỏa ra là \({5,2.10^{24}}MeV\)
=> Khi tổng hợp 2 hạt nhân He thì năng lượng tỏa ra sẽ là \(\Delta E = \dfrac{{{{2.5,2.10}^{24}}}}{{{{6,02.10}^{23}}}} = 17,3MeV\)
Hạt nhân \(^{{A_1}}X\) phóng xạ và biến thành một hạt nhân bền \(^{{A_2}}Y\). Coi khối lượng của các hạt nhân \(X, Y\) tính theo đơn vị \(u\) bằng số khối của chúng. Biết chất phóng xạ \(X\) có chu kì bán rã là \(T\). Ban đầu, có một mẫu \(X\) nguyên chất thì sau thời gian \(3T\), tỉ số giữa khối lượng của chất \(Y\) và khối lượng của chất :
+ Khối lượng Y sinh ra sau \(3T\): \({m_Y} = {m_{con}} = {m_0}.\dfrac{{{A_{con}}}}{{{A_{me}}}}\left( {1 - {2^{ - 3}}} \right) = {m_0}.\dfrac{{{A_2}}}{{{A_1}}}\left( {1 - {2^{ - 3}}} \right)=m_0.\dfrac{7}{8} \dfrac{{{A_2}}}{{{A_1}}}\)
+ Khối lượng \(X\) còn lại sau \(3T\): \({m_X} = {m_0}{.2^{ - 3}}\)
Tỉ số giữa khối lượng của chất \(Y\) và khối lượng của chất \(X\) là: \(\dfrac{{{m_Y}}}{{{m_X}}} = 7\dfrac{{{A_2}}}{{{A_1}}}\)
Một nơtron có động năng \(3 MeV\) bắn vào hạt nhân \(Li\) đang đứng yên, gây ra phản ứng hạt nhân \(_0^1n + _3^6Li \to _1^3H + \alpha \). Biết hạt \(\alpha \)và hạt nhân \(_1^3H\) bay ra theo các hướng hợp với hướng tới của nơtron những góc tương ứng bằng \(\theta = {25^0}C\) và \(\varphi = {15^0}\). Lấy tỉ số giữa các khối lượng hạt nhân bằng tỉ số giữa các số khối của chúng. Bỏ qua bức xạ gamma. Phản ứng trên
Theo bài ra ta có
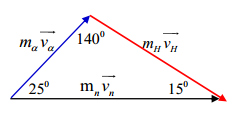
\(\begin{array}{*{20}{l}}{\dfrac{{{m_\alpha }{v_\alpha }}}{{\sin {{15}^0}}} = \dfrac{{{m_n}{v_n}}}{{\sin {{40}^0}}} = \dfrac{{{m_H}{v_H}}}{{\sin {{25}^0}}} = > \dfrac{{m_\alpha ^2v_\alpha ^2}}{{{{\sin }^2}{{15}^0}}} = \dfrac{{m_n^2v_n^2}}{{{{\sin }^2}{{45}^0}}} = \dfrac{{m_H^2v_H^2}}{{{{\sin }^2}{{25}^0}}}}\\{ = > \dfrac{{{m_\alpha }{{\rm{W}}_\alpha }}}{{{{\sin }^2}{{15}^0}}} = \dfrac{{{m_n}{{\rm{W}}_n}}}{{{{\sin }^2}{{40}^0}}} = \dfrac{{{m_H}{{\rm{W}}_H}}}{{{{\sin }^2}{{25}^0}}}}\\{ = > {{\rm{W}}_\alpha } = \dfrac{{1.3.{{\sin }^2}{{15}^0}}}{{4.{{\sin }^2}{{40}^0}}} = 0,122MeV;{{\rm{W}}_H} = \dfrac{{3.{{\sin }^2}{{25}^0}}}{{3.{{\sin }^2}{{40}^0}}} = 0,43MeV}\\{ = > \left\{ {\begin{array}{*{20}{l}}{{{\rm{W}}_\alpha } = 0,122MeV}\\{{{\rm{W}}_H} = 0,43MeV}\end{array}} \right. = > \Delta E = {{\rm{W}}_\alpha } + {{\rm{W}}_H} - {{\rm{W}}_n} = - 2,45MeV}\end{array}\)
Pôloni \(_{86}^{210}Po\) là chất phóng xạ, phát ra một hạt α và biến đổi thành hạt nhân \(X\). Ban đầu có \(7,0g\) hạt \(_{86}^{210}Po\) nguyên chất. Tại thời điểm \(t\) tỉ số giữa số hạt nhân \(X\) và số hạt nhân \(Po\) còn lại là \(3\). Khối lượng hạt nhân \(X\) được tạo thành đến thời điểm \(t\) là:
\(\begin{array}{l}\left\{ \begin{array}{l}{N_{con}} = {N_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)\\{N_{me}} = {N_0}{.2^{ - \dfrac{t}{T}}}\end{array} \right.\\ \to \dfrac{{{N_{con}}}}{{{N_{me}}}} = {2^{ - \dfrac{t}{T}}} - 1 = 3\\ \to t = 2T\end{array}\)
\(\begin{array}{l}{m_{con}} = {m_0}\dfrac{{{A_{con}}}}{{{A_{me}}}}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)\\ = 7.\dfrac{{206}}{{210}}\left( {1 - {2^{ - 2}}} \right) = 5,15g\end{array}\)
Trong một vụ thử hạt nhân, quả bom hạt nhân sử dụng sự phân hạch của đồng vị \(_{92}^{235}U\) với hệ số nhân nơtron là k ( k >1 ). Giả sử \(_{92}^{235}U\)phân hạch trong mỗi phản ứng tạo ra \(200{\rm{ }}MeV\). Coi lần đầu chỉ có một phân hạch và các lần phân hạch xảy ra đồng loạt. Sau 85 phân hạch thì quả bom giải phóng tổng cộng \(343,87\) triệu kWh. Giá trị của k là
Phương trình phản ứng: \(_0^1n + _{92}^{235}U \to X + Y + k_0^1n\)
Vậy cứ sau mỗi phản ứng lại tạo ra k hạt n để gây ra k phản ứng tiếp theo, hình thành chuỗi phản ứng theo cấp số nhân
Tổng số phản ứng là tổng của cấp số nhân ban đầu là 1, công bội là k, với 85 phản ứng
Từ đó, tổng năng lượng tỏa ra là:
\(\begin{array}{*{20}{l}}\begin{array}{l}\sum {pu = 1 + k + {k^2} + ... + {k^{84}}} \\ \Rightarrow \sum {E = \dfrac{{1.({k^{85}} - 1)}}{{k - 1}}{{.200.10}^6}{{.1,6.10}^{ - 19}} = {{343,87.10}^6}{{.10}^3}.60.60} \end{array}\\{ \Rightarrow k = 1,99999 \approx 2}\end{array}\)
Sử dụng tính Solve trong máy tính Casio fx 570 để tính ra k
Người ta trộn hai nguồn phóng xạ với nhau. Nguồn phóng xạ có hằng số phóng xạ \({\lambda _1}\), nguồn phóng xạ thứ 2 có hằng số phóng xạ \({\lambda _2}\). Biết \({\lambda _2} = 2{\lambda _1}\). Số hạt nhân ban đầu của nguồn thứ nhất gấp \(3\) lần số hạt nhân ban đầu của nguồn thứ 2. Hằng số phóng xạ của nguồn hỗn hợp là:
Gọi \({N_{01}}\) - số hạt nhân ban đầu của nguồn phóng xạ 1
\({N_{02}}\) - số hạt nhân ban đầu của nguồn phóng xạ 2
Ta có: \({N_{02}} = \dfrac{{{N_{01}}}}{2}\)
+ Sau thời gian t, số hạt nhân còn lại của mỗi nguồn là:
\(\left\{ \begin{array}{l}{N_1} = {N_{01}}.{e^{ - {\lambda _1}t}}\\{N_2} = {N_{02}}.{e^{ - {\lambda _2}t}} = \dfrac{{{N_{01}}}}{3}{e^{ - 2{\lambda _1}t}}\end{array} \right.\)
Tổng số hạt nhân còn lại của 2 nguồn:
\(N = {N_1} + {N_2} = {N_{01}}\left( {{e^{ - {\lambda _1}t}} + \dfrac{1}{3}{e^{ - 2{\lambda _1}t}}} \right)\)
\( = \dfrac{{{N_{01}}}}{3}\left( {3{e^{ - {\lambda _1}t}} + {e^{ - 2{\lambda _1}t}}} \right)\) (1)
+ Khi \(t = T\) (T là chu kì bán rã hỗn hợp) thì: \(N = \dfrac{1}{2}\left( {{N_{01}} + {N_{02}}} \right) = \dfrac{2}{3}{N_{01}}\) (2)
Từ (1) và (2), ta có: \(3.{e^{ - {\lambda _1}t}} + {e^{ - 2\lambda t}} = 2\)
Đặt \({e^{ - {\lambda _1}t}} = x\), ta được: \(3x + {x^2} = 2 \to \left( \begin{array}{l}x = 0,5615\\x = - 3,5615(loai)\end{array} \right.\)
Ta suy ra: \({e^{ - {\lambda _1}t}} = 0,5615\)
Ta có: \(t = T = \dfrac{1}{{{\lambda _1}}}\ln \dfrac{1}{{0,5615}}\)
Suy ra: \(\lambda = \dfrac{{\ln 2}}{T} = \dfrac{{\ln 2}}{{\dfrac{1}{{{\lambda _1}}}\ln \dfrac{1}{{0,5615}}}} = 1,20{\lambda _1}\)

