Một điện thoại di động hãng Samsung được treo bằng sợi dây cực mảnh trong một bình thủy tinh kín đã rút hết không khí. Điện thoại dùng số thuê bao 0914.815.918 vẫn đang nghe gọi bình thường và được cài đặt âm lượng lớn nhất với nhạc chuông bài hát “Người hãy quên em đi” do ca sĩ Mỹ Tâm. Thầy Nam đứng cạnh bình thủy tinh trên và dùng một điện thoại hãng OPPO gọi vào thuê bao 0344.815.918. Câu trả lời nào của Thầy Nam sau đây là câu nói thật:
+ Do sóng điện thoại là sóng điện từ.
Mà sóng điện từ truyền được trong môi trường chân không
=> Điện thoại vẫn liên lạc được
+ Sóng âm thì không truyền được trong môi trường chân không
=> Không nghe được nhạc chuông từ điện thoại phát ra
Một mạch dao động điện từ \(LC\) lí tưởng đang có dao động điện từ tự do. Điện áp cực đại giữa hai bản tụ là \({U_0} = 6\sqrt 3 V\). Không gian giữa hai bản tụ được lấp đầy bằng tấm điện môi có hằng số điện môi \(\varepsilon = 2\). Đúng lúc dòng điện tức thời trong mạch đạt giá trị cực đại thì rút nhanh tấm điện môi ra, sao cho tấm điện môi chỉ còn chiếm một nửa không gian giữa hai bản của tụ điện. Điện áp cực đại giữa hai bản tụ sau khi rút tấm điện môi là:
Ta có: \(C = \frac{{\varepsilon S}}{{{{9.10}^9}.4\pi d}}\)
+ Khi đặt trong điện môi có ε = 2:
\(C = {C_0} = \frac{{\varepsilon S}}{{{{9.10}^9}.4\pi d}}\)
+ Sau khi rút tấm điện môi để tấm điện môi chỉ còn chiếm một nửa không gian giữa hai bản tụ thì:
\({C_1} = \frac{{\varepsilon \frac{S}{2}}}{{{{9.10}^9}.4\pi }} = \frac{{{C_0}}}{2}\) (nửa đặt trong chất điện môi \(\varepsilon = 2\) )
\({C_2} = \frac{{\frac{S}{2}}}{{{{9.10}^9}.4\pi d}} = \frac{{{C_0}}}{4}\) (nửa đặt ngoài không khí \(\varepsilon = 1\) )
Ta có: \({C_1}//{C_2} \to {C_b} = {C_1} + {C_2} = \frac{{{C_0}}}{2} + \frac{{{C_0}}}{4} = \frac{{3{C_0}}}{4}\)
Lại có:
Năng lượng trước và sau khi rút tấm điện môi lần lượt là:
\(\left\{ \begin{array}{l}{{\rm{W}}_t} = \frac{{{C_0}U_0^2}}{2}\\{{\rm{W}}_s} = \frac{{{C_b}U_S^2}}{2} = \frac{{\frac{3}{4}{C_0}U_s^2}}{2}\end{array} \right.\)
Mặt khác:
\(\begin{array}{l}{{\rm{W}}_t} = {{\rm{W}}_s} \leftrightarrow \frac{{{C_0}U_0^2}}{2} = \frac{{\frac{3}{4}{C_0}U_s^2}}{2}\\ \to U_S^2 = \frac{4}{3}U_0^2 \to {U_s} = \frac{2}{{\sqrt 3 }}{U_0} = \frac{2}{{\sqrt 3 }}.6\sqrt 3 = 12V\end{array}\)
Vệ tinh viễn thông địa tĩnh Vinasat-1 nằm trên quỹ đạo địa tĩnh (là quỹ đạo tròn trên xích đạo của Trái Đất (vĩ độ \({0^0}\)) ở cách bề mặt Trái Đất \(35000{\rm{ }}km\) và có kinh độ \({132^0}\)Đ. Một sóng truyền hình phát từ Đài truyền hình Hà Nội ở tọa độ (\({21^0}01'\) B, \({105^0}48'\)Đ ) truyền lên vệ tinh, rồi tức thì truyền đến đài truyền hình Cần Thơ ở tọa độ (\({10^0}01'\)B, \({105^0}48'\)Đ) . Cho bán kính của Trái Đất là \(6400km\) và tốc độ truyền sóng trung bình là \(\dfrac{8}{3}{.10^8}m/s\). Bỏ qua độ cao của anten phát và aten thu ở các Đài truyền hình so với bán kình Trái Đất. Thời gian từ lúc truyền sóng đến nhận sóng gần giá trị nào nhất sau đây?
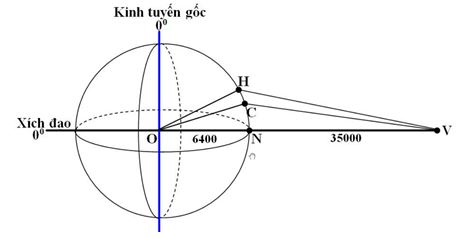
Kí hiệu vệ tinh là \(\left( V \right)\), do vệ tinh có vĩ độ \({0^0}\) nên đang nằm trên đường xích đạo
Hà Nội \(\left( H \right)\) và Cần Thơ \(\left( C \right)\) có cùng kinh độ, nhưng vĩ độ khác nhau, ta biểu diễn được trên hình.
+ \(\widehat {CON} = {10^0}01'\) chính là vĩ độ của \(\left( C \right)\)
Ta suy ra: \(CN = R.\widehat {CON} = 6400.\dfrac{{{{10}^0}01'.\pi }}{{180}} = 1118,87km\)
+ \(\widehat {HON} = {21^0}01'\) chính là vĩ độ của \(\left( H \right)\)
Ta suy ra: \(HN = R.\widehat {HON} = 6400.\dfrac{{{{21}^0}01'.\pi }}{{180}} = 2347,58km\)
Do \(\left( H \right)\) và \(\left( C \right)\) cùng kinh độ.
Xem \(\left( N \right)\) có cùng kinh độ với \(\left( H \right)\) và \(\left( C \right)\) và \(HC \bot OV\)
Ta có:
+ \(HV = \sqrt {H{N^2} + N{V^2}} = \sqrt {{{2347,58}^2} + {{35000}^2}} = 35078,64km\)
+ \(CV = \sqrt {C{N^2} + N{V^2}} = \sqrt {{{1118,87}^2} + {{35000}^2}} = 35017,88km\)
Quãng đường sóng truyền đi: \(s = HV + CV = 35078,64 + 35017,88 = 70096,52km = 70096520m\)
Vậy thời gian truyền sóng: \(t = \dfrac{s}{v} = \dfrac{{70096520}}{{\dfrac{8}{3}{{.10}^8}}} = 0,2628s\)
Trong một mạch dao động LC lý tưởng. Dòng điện trong mạch có biểu thức \(i = 12sin({10^5}\pi t)mA\) . Trong khoảng thời gian \(5\mu s\) kể từ thời điểm \(t{\rm{ }} = {\rm{ }}0\) , số electron chuyển động qua một tiết diện thẳng dây dẫn là:
- Cách 1:
+ Chu kì của mạch dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{{{10}^5}\pi }} = {2.10^{ - 5}}s\)
+ Tại thời điểm ban đầu: \(t = 0\), ta có: \(i = 0 \to \) \(\left| q \right| = {Q_0}\)
Ta có: \(5\mu s = \dfrac{T}{4}\) => số điện tích dịch chuyển là \({Q_0}\)
+ Số electron chuyển động qua một tiết diện thẳng dây dẫn là: \({n_e} = \dfrac{{{Q_0}}}{e}\)
Lại có \({Q_0} = \dfrac{{{I_0}}}{\omega }\)
=> Ta suy ra: \({n_e} = \dfrac{{\frac{{{I_0}}}{\omega }}}{e} = \dfrac{{{I_0}}}{{\omega .e}} = \dfrac{{{{12.10}^{ - 3}}}}{{{{10}^5}\pi .\left| { - {{1,6.10}^{ - 19}}} \right|}} = {2,39.10^{11}}\)
- Cách 2:
Áp dụng:
\(\begin{array}{l}q = ne = \int\limits_{{t_1}}^{{t_2}} {idt = \int\limits_0^{{{5.10}^{ - 6}}} {{{12.10}^{ - 3}}\sin \left( {{{10}^5}\pi t} \right)dt} } \\ = - \dfrac{{{{12.10}^{ - 3}}}}{{{{10}^5}\pi }}.c{\rm{os}}\left( {{{10}^5}\pi t} \right)\left| \begin{array}{l}{5.10^{ - 6}}\\0\end{array} \right.\\ = \dfrac{{{{12.10}^{ - 3}}}}{{{{10}^5}\pi }} = 3,{82.10^{ - 8}}\\ \to n = \dfrac{{3,{{82.10}^{ - 8}}}}{{\left| e \right|}} = \dfrac{{3,{{82.10}^{ - 8}}}}{{1,{{6.10}^{ - 19}}}} = 2,{38.10^{11}}\end{array}\)
Có hai mạch dao động điện từ lý tưởng đang có dao động điện từ tự do. Ở thời điểm \(t\) , gọi \({q_1}\) và \({q_2}\) lần lượt là điện tích của tụ điện trong mạch dao động thứ nhất và thứ hai. Biết \(36q_1^2 + 16q_2^2 = {24^2}{(nC)^2}.\) Ở thời điểm \(t{\rm{ }} = {\rm{ }}{t_1}\), trong mạch dao động thứ nhất: Điện tích của tụ điện \({q_1} = {\rm{ }}2,4nC\); cường độ dòng điện qua cuộn cảm \({i_1} = {\rm{ }}3,2mA\). Khi đó cường độ dòng điện qua cuộn cảm trong mạch dao động thứ hai là:
Theo đầu bài ta có: \(36q_1^2 + 16.q_2^2 = {24^2}\) (1)
Từ (1), ta suy ra: \( \Rightarrow {q_2} = \pm \sqrt {\frac{{{{24}^2} - 36q_1^2}}{{16}}} = \pm \sqrt {\frac{{{{24}^2} - 36.{{\left( {2,4} \right)}^2}}}{{16}}} = \pm 4,8nC\)
Đạo hàm hai vế của (1) theo thời gian ta có:
\(\begin{array}{l}36.2.{q_1}.\left( {{q_1}} \right)' + 16.2.{q_2}.\left( {{q_2}} \right)' = 0\\ \leftrightarrow 72{q_1}{i_1} + 32{q_2}{i_2} = 0\\ \to {i_2} = - \frac{{72{q_1}{i_1}}}{{32{q_2}}} = - \frac{{{{72.2,4.10}^{ - 9}}{{.3,2.10}^{ - 3}}}}{{32.\left( { \pm {{4,8.10}^{ - 9}}} \right)}} = \pm 3,6mA\end{array}\)
Cho hai mạch dao động \(LC\) có cùng tần số. Điện tích cực đại của tụ ở mạch thứ nhất và thứ hai lần lượt là \({Q_1}\) và \({Q_2}\) thỏa mãn \({Q_1} + {\rm{ }}{Q_2} = {\rm{ }}{8.10^{ - 6}}\). Tại một thời điểm mạch thứ nhất có điện tích và cường độ dòng điện là \({q_1}\) và \({i_1}\), mạch thứ hai có điện tích và cường độ dòng điện là \({q_2}\) và \({i_2}\) thỏa mãn \({q_1}{i_2} + {\rm{ }}{q_2}{i_1} = {\rm{ }}{6.10^{ - 9}}\). Giá trị nhỏ nhất của tần số dao động ở hai mạch là:
- Cách 1:
Gọi độ lệch pha giữa \({q_1}\) và \({q_2}\) là \(\Delta \varphi \), tại thời điểm \({q_1} = 0\) thì ${i_1} = {I_{01}} = \omega {Q_{01}}$ và \({q_2} = {Q_{02}}{\rm{cos}}\left( {\Delta \varphi } \right)\)
Thay vào phương trình \({q_1}{i_2} + {\rm{ }}{q_2}{i_1} = {\rm{ }}{6.10^{ - 9}}\) ta có:
\({Q_1}{Q_2}\omega c{\rm{os}}\Delta \varphi {\rm{ = 6}}{\rm{.1}}{{\rm{0}}^{{\rm{ - 9}}}} \Rightarrow \omega = \dfrac{{{{6.10}^{ - 9}}}}{{{Q_1}{Q_2}.c{\rm{os}}\Delta \varphi }}\)
Mặt khác ta có:
\({Q_1} + {Q_2} \geqslant 2\sqrt {{Q_1}{Q_2}} \Rightarrow {Q_1}{Q_2} \leqslant \dfrac{{{{\left( {{Q_1} + {Q_2}} \right)}^2}}}{4} = \dfrac{{{{\left( {{{8.10}^{ - 6}}} \right)}^2}}}{4} = 1,{6.10^{ - 11}}\)
Lại có: \(\left| {c{\rm{os}}\Delta \varphi } \right| \le 1\)
\( \to \omega \ge \dfrac{{{{6.10}^{ - 9}}}}{{{{1,6.10}^{ - 11}}}} = 375\) (1)
Thêm vào đó, ta có: \(\omega = 2\pi f \to f = \dfrac{\omega }{{2\pi }}\) (2)
Từ (1) và (2) ta suy ra: $f \geqslant \dfrac{{375}}{{2\pi }} = 59,68Hz$
- Cách 2:
Ta có: \({Q_1}.{Q_2} = \sqrt {q_1^2 + {{\left( {\dfrac{{{i_1}}}{\omega }} \right)}^2}} .\sqrt {{{\left( {\dfrac{{{i_2}}}{\omega }} \right)}^2} + q_2^2} \geqslant \dfrac{{{q_1}{i_2}}}{\omega } + \dfrac{{{q_2}{i_1}}}{\omega } = \dfrac{{{{6.10}^{ - 9}}}}{\omega }(1)\) (bất đẳng thức Bu-nhi-a-cốp-xki)
Mà \(\dfrac{{{Q_1} + {Q_2}}}{2} \ge \sqrt {{Q_1}.{Q_2}} \Leftrightarrow {\left( {\dfrac{{{Q_1} + {Q_2}}}{2}} \right)^2} \ge {Q_1}.{Q_2} \Leftrightarrow {\left( {\dfrac{{{{8.10}^{ - 6}}}}{2}} \right)^2} \ge {Q_1}.{Q_2}(2)\) (bất đẳng thức Cô-si)
Từ (1) và (2) =>\({\left( {\dfrac{{{{8.10}^{ - 6}}}}{2}} \right)^2} \ge \dfrac{{{{6.10}^{ - 9}}}}{\omega } \Rightarrow \omega \ge \dfrac{{{{4.6.10}^{ - 9}}}}{{{{64.10}^{ - 12}}}} = 375(rad/s)\)
Thêm vào đó, ta có: $\omega = 2\pi f \to f = \dfrac{\omega }{{2\pi }}$ (2)
Từ (1) và (2) ta suy ra: \(f \ge \dfrac{{375}}{{2\pi }} = 59,68Hz\)
Mạch chọn sóng của máy thu vô tuyến gồm tụ xoay \(C\) và cuộn thuần cảm \(L\). Tụ xoay có điện dung \(C\) tỉ lệ theo hàm số bậc nhất đối với góc xoay $\varphi $. Ban đầu khi chưa xoay tụ thì thì mạch thu được sóng có tần số \({f_0}\) , khi xoay tụ một góc ${\varphi _1}$ thì mạch thu được sóng có tần số \({f_1} = 0,5{f_0}\). Khi xoay tụ một góc \({\varphi _2}\) thì mạch thu được sóng có tần số \({f_2} = \dfrac{1}{3}{f_0}\). Tỉ số giữa hai góc xoay là:
Điện dung của tụ xoay được xác định bởi \({C_\varphi } = {C_0} + a\varphi \)
Tần số của mạch LC: \(f = \dfrac{1}{{2\pi \sqrt {L{C_\varphi }} }} \Rightarrow f \sim \dfrac{1}{{\sqrt {{C_\varphi }} }}\)
Ta có:
\(\left\{ \begin{array}{l}{f_0} \sim \dfrac{1}{{\sqrt {{C_0}} }}\\0,5{f_0} \sim \dfrac{1}{{\sqrt {{C_0} + a{\varphi _1}} }}\\\dfrac{1}{3}{f_0} \sim \dfrac{1}{{\sqrt {{C_0} + a{\varphi _2}} }}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}4 = \dfrac{{{C_0} + a{\varphi _1}}}{{{C_0}}} \Rightarrow a{\varphi _1} = 3\\9 = \dfrac{{{C_0} + a{\varphi _2}}}{{{C_0}}} \Rightarrow a{\varphi _2} = 8\end{array} \right. \Rightarrow \dfrac{{{\varphi _2}}}{{{\varphi _1}}} = \dfrac{8}{3}\)
Mạch chọn sóng của một máy thu vô tuyến điện gồm một cuộn cảm thuần và một tụ điện là tụ xoay \({C_x}\). Điện dung của tụ \({C_x}\) là hàm số bậc nhất của góc xoay. Khi chưa xoay tụ (góc xoay bằng \({0^0}\)) thì mạch thu được dóng có bước sóng \(10{\rm{ }}m\). Khi xoay tụ một góc là \({45^0}\) thì mạch thu được có bước sóng \(20{\rm{ }}m\) . Để mạch bắt được sóng có bước sóng \(30{\rm{ }}m\) thì phải xoay tụ thêm một góc bằng:
Ta có: \(C = a.\alpha + b\)
Cụ thể:
+ Khi \({\alpha _1} = {0^0}\) thì \({\lambda _1} = 10m\)
+ Khi \({\alpha _2} = {45^0}\) thì \({\lambda _2} = 20m\)
\({\left( {\dfrac{{{\lambda _1}}}{{{\lambda _2}}}} \right)^2} = \dfrac{{{C_1}}}{{{C_2}}} = \dfrac{b}{{45a + b}} \leftrightarrow \dfrac{1}{4} = \dfrac{b}{{45a + b}} \leftrightarrow b = 15a\)
+ Để mạch bắt được sóng có bước sóng \({\lambda _3} = 30cm\) thì góc xoay là \({\alpha _3}\).
Ta có: \({\left( {\dfrac{{{\lambda _3}}}{{{\lambda _1}}}} \right)^2} = \dfrac{{{C_3}}}{{{C_1}}} = \dfrac{{a.\alpha + b}}{b} \leftrightarrow 9 = \dfrac{{a.\alpha + 15a}}{{15a}} \leftrightarrow {\alpha _3} = {120^0}\)
=> Ta cần phải xoay tụ thêm góc \(\alpha = {\alpha _3} - {\alpha _2} = {120^0} - {45^0} = {75^0}\)
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E = 24V,r = 1\Omega \) , tụ điện có điện dung \(C = 100\mu F\), cuộn dây có hệ số tự cảm \(L = 0,2H\) và điện trở \({R_0} = 5\Omega \), điện trở \(R = 18\Omega \). Ban đầu khóa k đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khóa k. Nhiệt lượng tỏa ra trên điện trở \(R\) trong thời gian từ khi ngắt khóa k đến khi dao động mạch tắt hoàn toàn.
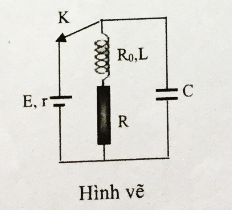
+ Khi khóa K đóng
Cường độ dòng điện chạy trong mạch : \(I = \frac{E}{{R + {R_0} + r}} = \frac{{24}}{{18 + 5 + 1}} = 1(A)\)
Hiệu điện thế hai đầu nguồn điện, cũng chính là hiệu điện thế hai đầu tụ: \(U = E - {\rm{Ir}} = 24 - 1 = 23(V)\)
+ Khi ngắt khóa K thì trong mạch có dao động điện từ tắt dần
Năng lượng điện từ ban đầu trong mạch dao động là:
\({\rm{W}} = {{\rm{W}}_C} + {{\rm{W}}_L} = \frac{1}{2}C{U^2} + \frac{1}{2}L{I^2} = \frac{1}{2}{.100.10^{ - 6}}{.23^2} + \frac{1}{2}{0,2.1^2} = 0,12645(J)\)
Khi dao động trong mạch tắt hoàn toàn thì năng lượng điện từ của mạch chuyển hóa hết thành nhiệt tỏa ra trên hai điện trở R và R0
Ta có: \(\left\{ \begin{array}{l}{Q_R} + {Q_{{R_0}}} = {\rm{W = 0}}{\rm{,12645}}\\\frac{{{Q_R}}}{{{Q_{{R_0}}}}} = \frac{R}{{{R_0}}} = \frac{{18}}{5}\end{array} \right. = > \left\{ \begin{array}{l}{Q_R} = 0,09896(J) = 98,96(mJ)\\{Q_{{R_0}}} = 0,02749(J)\end{array} \right.\)
Cho mạch điện như hình vẽ bên, nguồn điện một chiều có suất điện động \(E\) không đổi và điện trở trong \(r\),cuộn dây thuần cảm \(L\) và tụ điện có điện dung \(C{\rm{ }} = {\rm{ }}{2,5.10^{ - 7}}F\). Ban đầu khóa \(K\) mở, tụ chưa tích điện. Đóng khóa \(K\), khi mạch ổn định thì mở khóa \(K\). Lúc này trong mạch có dao động điện từ tự do với chu kì bằng \(\pi {.10^{ - 6}}s\) và hiệu điện thế cực đại trên tụ bằng \(2E\) .Giá trị của \(r\) bằng:
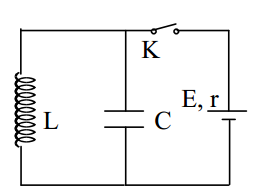
+ Khi \(K\) đóng, tụ điện được tích điện đến hiệu điện thế\({U_0} = {\rm{ }}2E\), dòng điện trong mạch lúc này là: \({I_0} = \dfrac{E}{r}\left( 1 \right)\)
+ Khi K mở, mạch LC dao động điện từ tự do, ta có:
\(\dfrac{1}{2}CU_0^2 = \dfrac{1}{2}LI_0^2 \Leftrightarrow CU_0^2 = LI_0^2 \Leftrightarrow {C^2}U_0^2 = LCI_0^2 = \dfrac{{{T^2}}}{{4{\pi ^2}}}I_0^2 \Leftrightarrow {I_0} = \dfrac{{2\pi C{U_0}}}{T}\left( 2 \right)\)
Từ (1) và (2) ta có : \(\dfrac{E}{r} = \dfrac{{2\pi C{U_0}}}{T} = \dfrac{{2\pi C.2E}}{T} \Rightarrow r = \dfrac{T}{{4\pi C}} = \dfrac{{\pi {{.10}^{ - 6}}}}{{4\pi {{.2,5.10}^{ - 7}}}} = 1\Omega \)
Theo mẫu nguyên tử Bo, mức năng lượng của trạng thái dừng thứ n của nguyên tử Hidro được xác định theo công thức \({E_n} = - \dfrac{{13,6}}{{{n^2}}}\left( {eV} \right);\left( {n = 1,2,3...} \right)\) Gọi R1 là bán kính quỹ đạo của e khi nguyên tử Hidro ở tạng thái dừng L. Khi nguyên tử ở trạng thái dừng ứng với bán kính bằng 9R1 thì tỷ số bước sóng lớn nhất và bước sóng nhỏ nhất của photon mà nguyên tử Hidro có thể phát xạ là:
R1 là bán kính quỹ đạo e ứng với trạng thái dừng L vậy \({r_1} = {2^2}{r_0}\)
Khi bán kính quỹ đạo là 9R1 ta có \(r = 9{r_1} = 9.4{r_0} = 36{r_0} = > n = 6\) ứng với trạng thái dừng P
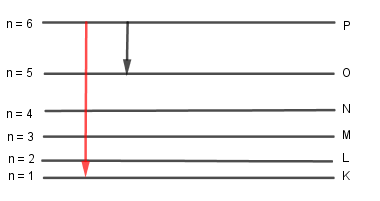
Bước sóng lớn nhất mà photon này có thể phát xạ ra khi nó chuyển mức năng lượng từ trạng thái P về trạng thái K là \(E = {E_P} - {E_0} = \dfrac{{{E_0}}}{{{6^2}}} - {E_0} = \dfrac{{35}}{{36}}{E_0} = \dfrac{{hc}}{{{\lambda _{max}}}} = > {\lambda _{max}} = \dfrac{{hc}}{{\dfrac{{35}}{{36}}{E_0}}}\)
Bước sóng ngắn nhất photon này có thể phát xạ ra khi nó chuyển mức năng lượng từ trạng thái P về trạng thái O là \(E = {E_P} - {E_O} = \dfrac{{{E_0}}}{{{6^2}}} - \dfrac{{{E_0}}}{5} = \dfrac{{11}}{{900}}{E_0} = \dfrac{{hc}}{{{\lambda _{\min }}}} = > {\lambda _{\min }} = \dfrac{{hc}}{{\dfrac{{11}}{{900}}{E_0}}}\)
Tỷ số giữa bước sóng ngắn lớn nhất và dài nhất là \(\dfrac{{{\lambda _{\min }}}}{{{\lambda _{max}}}} = \dfrac{{\dfrac{{hc}}{{\dfrac{{35}}{{36}}{E_0}}}}}{{\dfrac{{hc}}{{\dfrac{{11}}{{900}}{E_0}}}}} = \dfrac{{35}}{{36}}.\dfrac{{900}}{{11}} = \dfrac{{875}}{{11}}\)
Vệ tinh địa tĩnh là vệ tinh mà ta quan sát nó từ Trái Đất dường như nó đứng im trên không. Điều kiện để có vệ tinh địa tĩnh là phải phóng vệ tinh sao cho mặt phẳng quay của nó nằm trong mặt phẳng xích đạo của Trái Đất, chiều chuyển động theo chiều quay của Trái Đất và có chu kì quay đúng bằng chu kì tự quay của Trái Đất là 24 giờ.Cho bán kính Trái Đất R = 6400 km. Biết vệ tinh quay trên quỹ đạo với tốc độ dài 3,68 km/s. Khi vệ tinh phát sóng điện tử, tỉ số giữa thời gian dài nhất và ngắn nhất sóng đến được mặt đất là:
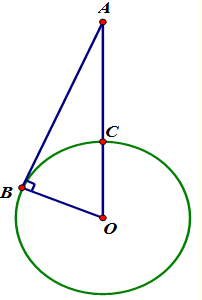
Ta có:
\(v = \omega d \Rightarrow d = \frac{v}{\omega } = \frac{{vT}}{{2\pi }} = OA\)
\( \Rightarrow AC = OA - OC = \frac{{vT}}{{2\pi }} - R\)
Lại có:
\(AB = \sqrt {O{A^2} - O{B^2}} = \sqrt {{{\left( {\frac{{vT}}{{2\pi }}} \right)}^2} - {R^2}} \)
Thời gian sóng truyền đến điểm B trên Trái Đất là dài nhất và đến điểm C là ngắn nhất.
Ta có: \({t_{\max }} = \frac{{{s_{\max }}}}{c};\,{t_{\min }} = \frac{{{s_{\min }}}}{c}\)
\( \Rightarrow \frac{{{t_{\max }}}}{{{t_{\min }}}} = \frac{{{s_{\max }}}}{{{s_{\min }}}} = \frac{{AB}}{{AC}} = \sqrt {\frac{{\frac{{vT}}{{2\pi }} + R}}{{\frac{{vT}}{{2\pi }} - R}}} = 1,136\)

