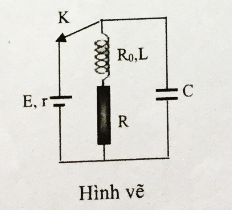
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E = 24V,r = 1\Omega \) , tụ điện có điện dung \(C = 100\mu F\), cuộn dây có hệ số tự cảm \(L = 0,2H\) và điện trở \({R_0} = 5\Omega \), điện trở \(R = 18\Omega \). Ban đầu khóa k đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khóa k. Nhiệt lượng tỏa ra trên điện trở \(R\) trong thời gian từ khi ngắt khóa k đến khi dao động mạch tắt hoàn toàn.

Một điện thoại di động hãng Samsung được treo bằng sợi dây cực mảnh trong một bình thủy tinh kín đã rút hết không khí. Điện thoại dùng số thuê bao 0914.815.918  vẫn đang nghe gọi bình thường và được cài đặt âm lượng lớn nhất với nhạc chuông bài hát “Người hãy quên em đi” do ca sĩ Mỹ Tâm. Thầy Nam đứng cạnh bình thủy tinh trên và dùng một điện thoại hãng OPPO gọi vào thuê bao 0344.815.918. Câu trả lời nào của Thầy Nam sau đây là câu nói thật:

Một mạch dao động điện từ \(LC\) lí tưởng đang có dao động điện từ tự do. Điện áp cực đại giữa hai bản tụ là \({U_0} = 6\sqrt 3 V\). Không gian giữa hai bản tụ được lấp đầy bằng tấm điện môi có hằng số điện môi \(\varepsilon  = 2\). Đúng lúc dòng điện tức thời trong mạch đạt giá trị cực đại thì rút nhanh tấm điện môi ra, sao cho tấm điện môi chỉ còn chiếm một nửa không gian giữa hai bản của tụ điện. Điện áp cực đại giữa hai bản tụ sau khi rút tấm điện môi là:

Vệ tinh viễn thông địa tĩnh Vinasat-1 nằm trên quỹ đạo địa tĩnh (là quỹ đạo tròn trên xích đạo của Trái Đất (vĩ độ \({0^0}\)) ở cách bề mặt Trái Đất \(35000{\rm{ }}km\) và có kinh độ \({132^0}\)Đ. Một sóng truyền hình phát từ Đài truyền hình Hà Nội ở tọa độ (\({21^0}01'\) B, \({105^0}48'\)Đ ) truyền lên vệ tinh, rồi tức thì truyền đến đài truyền hình Cần Thơ ở tọa độ (\({10^0}01'\)B, \({105^0}48'\)Đ) . Cho bán kính của Trái Đất là \(6400km\) và tốc độ truyền sóng trung bình là \(\dfrac{8}{3}{.10^8}m/s\). Bỏ qua độ cao của anten phát và aten thu ở các Đài truyền hình so với bán kình Trái Đất. Thời gian từ lúc truyền sóng đến nhận sóng gần giá trị nào nhất sau đây?

Trong một mạch dao động LC lý tưởng. Dòng điện trong mạch có biểu thức \(i = 12sin({10^5}\pi t)mA\) . Trong khoảng thời gian \(5\mu s\) kể từ thời điểm \(t{\rm{ }} = {\rm{ }}0\) , số electron chuyển động qua một tiết diện thẳng dây dẫn là:

Có hai mạch dao động điện từ lý tưởng đang có dao động điện từ tự do. Ở thời điểm \(t\) , gọi \({q_1}\) và \({q_2}\) lần lượt là điện tích của tụ điện trong mạch dao động thứ nhất và thứ hai. Biết \(36q_1^2 + 16q_2^2 = {24^2}{(nC)^2}.\) Ở thời điểm \(t{\rm{ }} = {\rm{ }}{t_1}\), trong mạch dao động thứ nhất: Điện tích của tụ điện \({q_1} = {\rm{ }}2,4nC\); cường độ dòng điện qua cuộn cảm \({i_1} = {\rm{ }}3,2mA\). Khi đó cường độ dòng điện qua cuộn cảm trong mạch dao động thứ hai là:

Cho hai mạch dao động \(LC\) có cùng tần số. Điện tích cực đại của tụ ở mạch thứ nhất và thứ hai lần lượt là \({Q_1}\) và \({Q_2}\) thỏa mãn \({Q_1} + {\rm{ }}{Q_2} = {\rm{ }}{8.10^{ - 6}}\). Tại một thời điểm mạch thứ nhất có điện tích và cường độ dòng điện là \({q_1}\) và \({i_1}\), mạch thứ hai có điện tích và cường độ dòng điện là \({q_2}\) và \({i_2}\) thỏa mãn \({q_1}{i_2} + {\rm{ }}{q_2}{i_1} = {\rm{ }}{6.10^{ - 9}}\). Giá trị nhỏ nhất của tần số dao động ở hai mạch là:

Mạch chọn sóng của máy thu vô tuyến gồm tụ xoay \(C\) và cuộn thuần cảm \(L\). Tụ xoay có điện dung \(C\) tỉ lệ theo hàm số bậc nhất đối với góc xoay $\varphi $. Ban đầu khi chưa xoay tụ thì thì mạch thu được sóng có tần số \({f_0}\) , khi xoay tụ một góc ${\varphi _1}$ thì mạch thu được sóng có tần số \({f_1} = 0,5{f_0}\). Khi xoay tụ một góc \({\varphi _2}\) thì mạch thu được sóng có tần số \({f_2} = \dfrac{1}{3}{f_0}\). Tỉ số giữa hai góc xoay là: