Bài tập phương trình dao động mạch LC (q - u - i)

+ Chu kì dao động:

\(T = 2\pi \sqrt {LC}  = 2\pi \sqrt {{{1.10.10}^{ - 6}}}  = 0,02{\rm{s}}\)

+ Thời gian ngắn nhất điện tích trên tụ từ giá trị cực đại về 0 là:

\(\dfrac{T}{4} = \dfrac{1}{{200}}s\)

Tại thời điểm \(t:i = 2mA.\)

Tại thời điểm \(t + \frac{{\pi \sqrt {LC} }}{2}:\,\,\,u = 1V\)

Ta có: \(\Delta t = \frac{{\pi \sqrt {LC} }}{2} = \frac{\pi }{{2\omega }} = \frac{{2\pi }}{\omega }.\frac{1}{4} = \frac{T}{4}\)

Mạch chứa L, C thì I và U vuông pha, ta có:

\(\frac{{{i_1}}}{{{I_0}}} = \frac{{{u_2}}}{{{U_0}}} \Leftrightarrow \frac{{0,2}}{{{I_0}}} = \frac{1}{{{I_0}\sqrt {\frac{L}{C}} }} \Rightarrow C = 1,{6.10^{ - 7}}F\)

Biểu thức của điện tích và cường độ dòng điện:

\(\left\{ \begin{array}{l}q = {Q_0}.\cos \left( {\omega t + \varphi } \right)(C)\\i = q' = \omega {Q_0}.\cos \left( {\omega t + \varphi  + \dfrac{\pi }{2}} \right)(A)\end{array} \right.\)

\( \Rightarrow \) \(q\) biến thiên điều hòa theo thời gian với cùng tần số trễ pha \(\dfrac{\pi }{2}\)  so với \(i\).

Kể từ lúc nối (pha của q là 0) đến khi điện tích trên tụ có giá trị bằng một nửa giá trị ban đầu (pha của q là \(\frac{\pi }{3}\)) => Thời gian ngắn nhất là:

\(t = \dfrac{T}{6} = \frac{{2\pi \sqrt {LC} }}{6} = \dfrac{{2\pi \sqrt {{{10.10}^{ - 6}}.1} }}{6} = \dfrac{1}{{300}}s\)

\(q = {Q_0}\cos (\omega t + \varphi )\)

Biểu thức của cường độ dòng điện trong mạch: \(i = q' = \omega {Q_0}\cos (\omega t + \varphi  + \dfrac{\pi }{2})\)

=> cường độ dòng điện sớm pha hơn điện tích trong mạch một góc \(\dfrac{\pi }{2}\)

\(q = {Q_0}\cos (\omega t + \varphi )\)

Biểu thức của hiện điện thế trong mạch là: \(u = \dfrac{{{Q_0}}}{C}\cos (\omega t + \varphi )\)

=> điện áp cùng pha với điện tích trong mạch

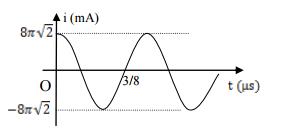
+ Nhìn vào đồ thị ta thấy \({I_0} = 8\pi \sqrt 2 mA\)

+ Khoảng thời gian \(t = \dfrac{3}{8}\mu s = \dfrac{{3T}}{4} =  > T = 0,5\mu s =  > \omega  = 4\pi {.10^6}rad/s\)

+ Điện tích cực đại: \({q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{8\pi \sqrt 2 {{.10}^{ - 3}}}}{{4\pi {{.10}^6}}} = 2\sqrt 2 {.10^{ - 9}}C = 2\sqrt 2 nC\)

+ Thời điểm t = 0 thì \(i = {I_0} =  > {\varphi _{0i}} = 0\)

+ Vậy ta có \(i = 8\pi \sqrt 2 {.10^{ - 3}}\cos 4\pi {.10^6}t\left( A \right) =  > q = 2\sqrt 2 {.10^{ - 9}}.cos\left( {4\pi {{.10}^6}.t - \dfrac{\pi }{2}} \right)\left( A \right)\)

+ Tần số góc của dao động: \(\omega  = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {{{10}^{ - 3}}{{.10}^{ - 9}}} }} = {10^6}\left( {rad/s} \right)\)

+ Theo đề bài ta có: \(U = 4V \Rightarrow {U_0} = \sqrt 2 U = 4\sqrt 2 V\)

+ Tại thời điểm ban đầu ta có, \({u_C} = 2V\)

Ta suy ra:

\(\begin{array}{l}{u_C} = {U_0}cos\varphi \\ \Leftrightarrow 2\sqrt 2  = 4\sqrt 2 cos\varphi \\ \Rightarrow cos\varphi  = \dfrac{1}{2} \Rightarrow \varphi  =  \pm \dfrac{\pi }{3}\end{array}\)

Tại thời điểm đó tụ điện đang được nạp điện (tức là đang tăng)

Ta suy ra \(\varphi  =  - \dfrac{\pi }{3}\left( {rad} \right)\)

Vậy phương trình điện áp trên tụ điện: \(u = 4\sqrt 2 cos\left( {{{10}^6}t - \dfrac{\pi }{3}} \right)V\)

Giả sử phương trình điện tích là :  \(q = {Q_0}.\cos \left( {\omega t + \varphi } \right)\)

Phương trình cường độ dòng điện là :  \(i = q' =  - \omega .{Q_0}.\sin \left( {\omega t + \varphi } \right) = {I_0}.\cos \left( {\omega t + \varphi  + \dfrac{\pi }{2}} \right)\)

Gốc thời gian là lúc tụ đang phóng điện tức là q đang giảm, ta có hình vẽ:

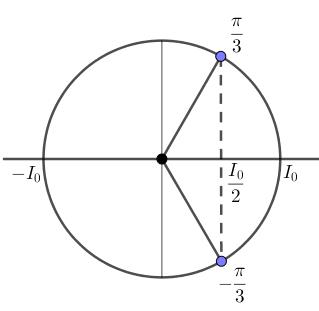
+ Vì q đang giảm nên I đang tăng => pha ban đầu của dòng điện \({\varphi _i} =  - \dfrac{\pi }{3}\)

=> Phương trình của I là :  \(i = {I_0}.\cos \left( {\omega t - \dfrac{\pi }{3}} \right)\)

+ Với tần số góc:  \(\omega  = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {{{2.10}^{ - 3}}{{.2.10}^{ - 9}}} }} = {5.10^5}rad/s\)

+ Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì năng lượng từ trường cũng bằng một nửa năng lượng từ trường cực đại nên :

\(\begin{array}{*{20}{l}}{\dfrac{1}{2}L.{i^2} = \dfrac{1}{2}.\dfrac{1}{2}.L.I_0^2}\\{ =  > I_0^2 = 2{i^2} = 2.{{\sqrt 2 }^2} = 4 =  > {I_0} = 2A}\end{array}\)

Vậy phương trình của dòng điện i là: \(i = 2.\cos \left( {{{5.10}^5}t - \dfrac{\pi }{3}} \right)A\)

+ Tần số góc của dao động: \(\omega  = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {{{10}^{ - 3}}{{.10.10}^{ - 6}}} }} = {10^4}\left( {rad/s} \right)\)

+ Theo đề bài, ta có \(I = 1mA \Rightarrow {I_0} = \sqrt 2 I = \sqrt 2 mA\)

+ Tại thời điểm ban đầu \(t = 0\) thì \({{\rm{W}}_d} = 3{W_t}\)

Ta có:

\(\begin{array}{l}{\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = {W_d} + \dfrac{{{{\rm{W}}_d}}}{3} = \dfrac{4}{3}{W_d}\\ \Rightarrow {{\rm{W}}_d} = \dfrac{{{\rm{3W}}}}{4}\\ \Leftrightarrow \dfrac{{{q^2}}}{{2C}} = \dfrac{3}{4}\dfrac{{q_0^2}}{{2C}} \Rightarrow q = \dfrac{{\sqrt 3 {q_0}}}{2}\end{array}\)

Lại có:

\(\begin{array}{l}q = {q_0}cos\varphi  \Leftrightarrow \dfrac{{\sqrt 3 }}{2}{q_0} = {q_0}cos\varphi \\ \Rightarrow cos\varphi  = \dfrac{{\sqrt 3 }}{2} \Rightarrow \varphi  =  \pm \dfrac{\pi }{6}\end{array}\) 

Vì tụ đang phóng điện nên => \(\varphi  = \dfrac{\pi }{6}\)

Ta có cường độ dòng điện sớm pha hơn điện tích một góc \(\dfrac{\pi }{2}\)

\( \Rightarrow {\varphi _i} = \dfrac{\pi }{6} + \dfrac{\pi }{2} = \dfrac{{2\pi }}{3}\left( {rad} \right)\)

Vậy phương trình cường độ dòng điện trong mạch là: \(i = \sqrt 2 \cos \left( {{{10}^4}t + \dfrac{{2\pi }}{3}} \right)mA\)

Ta có:

+ Tần số góc của dao động: \(\omega  = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {{{0,25.10}^{ - 3}}{{.40.10}^{ - 12}}} }} = {10^7}\left( {rad/s} \right)\)

+ Cường độ dòng điện cực đại: \({I_0} = \omega {q_0}\)

=> Điện tích cực đại trên tụ: \({q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{{{50.10}^{ - 3}}}}{{{{10}^7}}} = {5.10^{ - 9}}C\)

+ Tại thời điểm ban đầu, cường độ dòng điện có giá trị cực đại và đang giảm => điện tích trên bản tụ bằng 0 và đang tăng

\( \Rightarrow {\varphi _q} =  - \dfrac{\pi }{2}\)

Vậy phương trình điện tích trên bản tụ: \(q = {5.10^{ - 9}}cos\left( {{{10}^7}t - \dfrac{\pi }{2}} \right)C\)

+ Khi năng lượng điện trường cực đại :\({{\rm{W}}_{LC}} = {{\rm{W}}_{C\max }}\) khi đó \(u =  \pm {U_0}\)

+ Khi một nửa năng lượng điện trường cực đại trong tụ chuyển thành năng lượng từ trường trong cuộn cảm, tức năng lượng điện từ chuyển thành năng lượng từ trường nghĩa là \({{\rm{W}}_C}\) giảm từ \({\rm{W}}\)  xuống \(\dfrac{{\rm{W}}}{2}\) trong thời gian \({t_0}\):

\({{\rm{W}}_L} = \dfrac{{{{\rm{W}}_{C\max }}}}{2} = \dfrac{{{{\rm{W}}_{LC}}}}{2} \Rightarrow {{\rm{W}}_C} = \dfrac{{{{\rm{W}}_{LC}}}}{2} \Leftrightarrow \dfrac{{C{u^2}}}{2} = \dfrac{1}{2}\dfrac{{CU_0^2}}{2} \Rightarrow u =  \pm \dfrac{{{U_0}}}{{\sqrt 2 }}\)

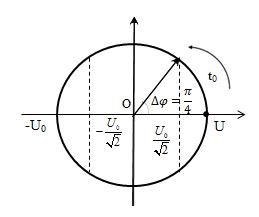
\( \Rightarrow {t_0} = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{\pi }{4}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{T}{8} \Rightarrow T = 8{t_0}\)

=> Chu kì dao động của mạch \(T{\rm{ }} = {\rm{ }}8{t_0}\)

+ Theo bài ra ta có khoảng thời gian ngắn nhất kể từ  khi tụ bắt đầu phóng điện đến khi điện áp tức thời giữa hai bản tụ bằng điện áp hiệu dụng là

$u = \frac{q}{C} = {\rm{}} > u = \frac{{{U_0}}}{{\sqrt 2 }} = {\rm{}} > q = \frac{{{Q_0}}}{{\sqrt 2 }}$

+ Biểu diễn trên đường tròn lượng giác ta được : \(t = \dfrac{T}{8}\)

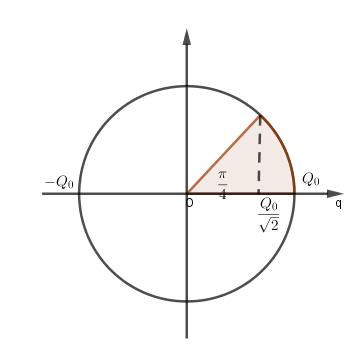
Vậy tần số dao động của mạch là   

$\frac{T}{8} = 0,5\mu s = {\rm{}} > T = 4\mu s = {\rm{}} > f = \frac{1}{T} = 250000Hz = 250kHz$$u = \frac{q}{C} = {\rm{}} > u = \frac{{{U_0}}}{{\sqrt 2 }} = {\rm{}} > q = \frac{{{Q_0}}}{{\sqrt 2 }}$

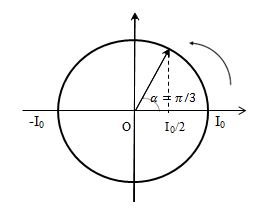
- Khoảng thời gian để cường độ dòng điện qua cuộn cảm giảm từ độ lớn cực đại xuống còn một nửa độ lớn cực đại là: \(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{\pi }{3}.\dfrac{T}{{2\pi }} = \dfrac{T}{6} = 800\mu s \Rightarrow T = 4800\mu s\) 

- Năng lượng từ trường trong mạch cực đại: \(i =  \pm {I_0}\)

- Năng lượng từ trường bằng nửa giá trị cực đại: \(\dfrac{{L{i^2}}}{2} = \dfrac{1}{2}.\dfrac{{LI_0^2}}{2} \Rightarrow i =  \pm \dfrac{{{I_0}}}{{\sqrt 2 }}\)

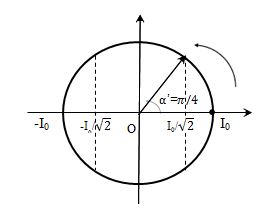
=> Khoảng thời gian ngắn nhất để năng lượng từ trường trong mạch giảm từ độ lớn cực đại xuống còn một nửa giá trị đó là: \(\Delta t' = \dfrac{{\alpha '}}{\omega } = \dfrac{\pi }{4}.\dfrac{T}{{2\pi }} = \dfrac{T}{8} = \dfrac{{4800}}{8} = 600\mu s\)

Biểu diễn trên đường tròn lượng giác ta có:

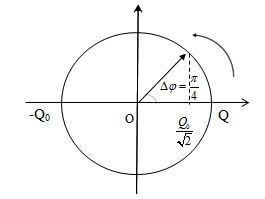
Theo đề bài, sau khoảng thời gian ngắn nhất Δt thì điện tích trên bản tụ giảm từ giá trị cực đại xuống nửa giá trị cực đại \( \Rightarrow \Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\Delta \varphi }}{{\dfrac{{2\pi }}{T}}} = \dfrac{{\dfrac{\pi }{4}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{T}{8} \Rightarrow T = 8\Delta t\)

Chu kì dao động \(T = 8\Delta t\)

Biểu diễn trên đường tròn lượng giác ta có:

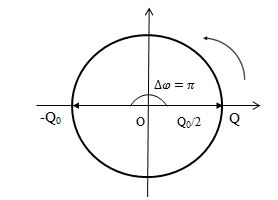
Theo bài ra ta tính được: \(T = 2\pi \sqrt {LC}  = 2\pi \sqrt {{{5.10}^{ - 6}}{{.5.10}^{ - 6}}}  = \pi {.10^{ - 5}}s\)

→ Thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là :

\(\Delta t = \dfrac{{\Delta \varphi }}{\omega } = \pi .\dfrac{T}{{2\pi }} = \dfrac{T}{2} = \dfrac{{\pi {{.10}^{ - 5}}}}{2} = 5\pi {.10^{ - 6}}s\)

Năng lượng điện từ: \({{\rm{W}}_0} = \dfrac{{CU_0^2}}{2} = \dfrac{{C{E^2}}}{2} \Rightarrow C = \dfrac{{2{{\rm{W}}_0}}}{{{E^2}}} = {1,25.10^{ - 7}}F\)

\({{\rm{W}}_{LC}} = {{\rm{W}}_L} + {{\rm{W}}_C} \Leftrightarrow {{\rm{W}}_{LC}} = 2{{\rm{W}}_C} \Leftrightarrow \dfrac{{CU_0^2}}{2} = 2.\dfrac{{C{u^2}}}{2} \Rightarrow u =  \pm \dfrac{{{U_0}}}{{\sqrt 2 }}\)

Khi điện áp giữa hai đầu tụ điện \(u =  \pm \dfrac{{{U_0}}}{{\sqrt 2 }}\) thì năng lượng điện trường bằng năng lượng từ trường.

Biểu diễn trên đường tròn lượng giác:

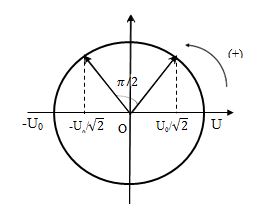
Góc quét được: \(\alpha  = \dfrac{\pi }{2} \Rightarrow \Delta t = \dfrac{{\Delta \varphi }}{\omega } = \Delta \varphi .\dfrac{T}{{2\pi }} = \dfrac{\pi }{2}.\dfrac{T}{{2\pi }} = \dfrac{T}{4}\)

Cứ sau khoảng thời gian T/4 thì năng lượng điện trường lại bằng năng lượng từ trường

\( \Rightarrow \dfrac{T}{4} = {10^6}s \Rightarrow T = {4.10^{ - 6}}s = 2\pi \sqrt {LC}  \Rightarrow L = \dfrac{{{T^2}}}{{4{\pi ^2}C}} = {3,24.10^{ - 6}}H\)

Từ công thức năng lượng: \(\dfrac{1}{2}LI_0^2 = {{\rm{W}}_0} \Rightarrow {I_0} = \sqrt {\dfrac{{2{W_0}}}{L}}  = 0,785A\)

\(\begin{array}{l}T = 2\pi \sqrt {LC}  = {8.10^{ - 7}}(s)\\{{\rm{W}}_C} = 3{W_L} = \dfrac{3}{4}{\rm{W}} \to {{\rm{q}}^2} = \dfrac{3}{4}q_0^2 \to q =  \pm \dfrac{{\sqrt 3 }}{2}{q_0}\end{array}\)

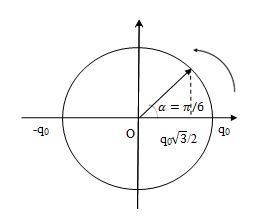
Thời gian từ lúc tụ bắt đầu phóng điện (q = q₀) đến lúc \(q =  \pm \dfrac{{\sqrt 3 }}{2}{q_0}\)là:

 \(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{\pi }{6}.\dfrac{T}{{2\pi }} = \dfrac{T}{{12}} = \dfrac{{{{8.10}^{ - 7}}}}{{12}} = \dfrac{{{{10}^{ - 6}}}}{{15}}(s)\)

+ Chu kì của mạch dao động:  \(T = 2\pi \sqrt {LC}  = 2\pi \sqrt {{{50.10}^{ - 6}}{{.5.10}^{ - 9}}}  = \pi {10^{ - 6}}\left( s \right) = \pi \left( {\mu s} \right)\)

+ Điện tích cực đại trên mỗi bản tụ: \({Q_0} = C{U_0} = C.E = 5.8 = 40{\rm{ }}nC\)

+ Ban đầu: Bản B nối với cực âm ta suy ra: \({q_B} =  - {Q_0} =  - 40nC\)

Biểu diễn trên đường tròn lượng giác ta có:

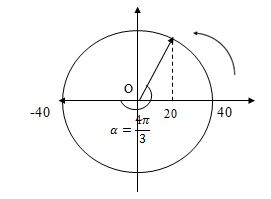
Thời gian ngắn nhất để \({q_B} =  - {Q_0}\) đến \({q_B} = 20nC = \dfrac{{{Q_0}}}{2}\) (phóng điện) là: \(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{{4\pi }}{3}.\dfrac{T}{{2\pi }} = \dfrac{{2T}}{3} = 2,1\mu s\)

+ Chu kì dao động của mạch: \(T = 2\pi \sqrt {LC}  = {4.10^{ - 5}}s\)

+ Tại thời điểm ban đầu: \({i_1} = I = \dfrac{{{I_0}}}{{\sqrt 2 }}\)

Thời điểm năng lượng điện bằng 3 lần năng lượng từ: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = 4{W_L} \Leftrightarrow 4\dfrac{{Li_2^2}}{2} = \dfrac{{LI_0^2}}{2} \Rightarrow {i_2} =  \pm \dfrac{{{I_0}}}{2}\)

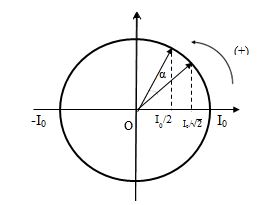
Dựa vào hình vẽ ta tính được góc quét \(\alpha  = \dfrac{\pi }{3} - \dfrac{\pi }{4} = \dfrac{\pi }{{12}}rad\)

Thời điểm ngay sau đó năng lượng điện bằng 3 lần năng lượng từ là:

\(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{\pi }{{12}}.\dfrac{T}{{2\pi }} = \dfrac{T}{{24}} = \dfrac{5}{3}\mu s\)