Một mạch dao động LC có \(L = 2mH,C = 8pF,\) lấy \({\pi ^2} = 10.\) Thời gian từ lúc tụ bắt đầu phóng điện đến lúc có năng lượng điện trường bằng ba lần năng lượng từ trường là:
Trả lời bởi giáo viên
\(\begin{array}{l}T = 2\pi \sqrt {LC} = {8.10^{ - 7}}(s)\\{{\rm{W}}_C} = 3{W_L} = \dfrac{3}{4}{\rm{W}} \to {{\rm{q}}^2} = \dfrac{3}{4}q_0^2 \to q = \pm \dfrac{{\sqrt 3 }}{2}{q_0}\end{array}\)
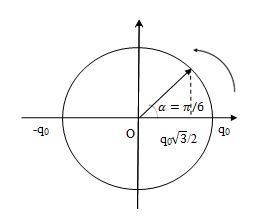
Thời gian từ lúc tụ bắt đầu phóng điện (q = q0) đến lúc \(q = \pm \dfrac{{\sqrt 3 }}{2}{q_0}\)là:
\(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{\pi }{6}.\dfrac{T}{{2\pi }} = \dfrac{T}{{12}} = \dfrac{{{{8.10}^{ - 7}}}}{{12}} = \dfrac{{{{10}^{ - 6}}}}{{15}}(s)\)
Hướng dẫn giải:
Sử dụng lí thuyết về năng lượng dao động điện từ \(W = {W_L} + {W_C}\) và vòng tròn lượng giác