Câu hỏi:
2 năm trước
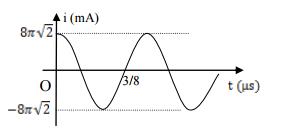
Dao động điện từ tự do trong mạch trong mạch LC có đường biểu diễn sự phụ thuộc của cường độ dòng điện qua cuộn dây theo thời gian như hình vẽ. Biểu thức điện tích tức thời trên tụ điện là
Trả lời bởi giáo viên
Đáp án đúng: c
+ Nhìn vào đồ thị ta thấy \({I_0} = 8\pi \sqrt 2 mA\)
+ Khoảng thời gian \(t = \dfrac{3}{8}\mu s = \dfrac{{3T}}{4} = > T = 0,5\mu s = > \omega = 4\pi {.10^6}rad/s\)
+ Điện tích cực đại: \({q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{8\pi \sqrt 2 {{.10}^{ - 3}}}}{{4\pi {{.10}^6}}} = 2\sqrt 2 {.10^{ - 9}}C = 2\sqrt 2 nC\)
+ Thời điểm t = 0 thì \(i = {I_0} = > {\varphi _{0i}} = 0\)
+ Vậy ta có \(i = 8\pi \sqrt 2 {.10^{ - 3}}\cos 4\pi {.10^6}t\left( A \right) = > q = 2\sqrt 2 {.10^{ - 9}}.cos\left( {4\pi {{.10}^6}.t - \dfrac{\pi }{2}} \right)\left( A \right)\)
Hướng dẫn giải:
+ Đọc đồ thị i - t
+ Áp dụng mối liên hệ giữa cường độ dòng điện và điện tích trong mạch : i = q'
=> điện tích \(q\) trễ pha \(\dfrac{\pi }{2}\) so với cường độ dòng điện hay \({\varphi _q} = {\varphi _i} - \dfrac{\pi }{2}\)
+ Viết phương trình điện tích \(q = {q_0}cos\left( {\omega t + {\varphi _q}} \right)\)
Câu hỏi khác
- Bài tập mạch dao động LC các đại lượng đặc trưng có lời giải MÔN LÝ lớp 12
- Bài tập năng lượng của mạch dao động LC có lời giải MÔN LÝ lớp 12
- Bài tập phương trình dao động mạch LC q,u,i có lời giải MÔN LÝ lớp 12
- Bài tập điện từ trường - sóng điện từ lý 12 có lời giải
- Bài tập các loại dao động lý 12 có lời giải
