Câu hỏi:
2 năm trước
Một mạch dao động điện từ tự do LC. Một nửa năng lượng điện trường cực đại trong tụ chuyển thành năng lượng từ trong cuộn cảm mất thời gian \({t_0}\). Chu kì dao động điện từ trong mạch là
Trả lời bởi giáo viên
Đáp án đúng: c
+ Khi năng lượng điện trường cực đại :\({{\rm{W}}_{LC}} = {{\rm{W}}_{C\max }}\) khi đó \(u = \pm {U_0}\)
+ Khi một nửa năng lượng điện trường cực đại trong tụ chuyển thành năng lượng từ trường trong cuộn cảm, tức năng lượng điện từ chuyển thành năng lượng từ trường nghĩa là \({{\rm{W}}_C}\) giảm từ \({\rm{W}}\) xuống \(\dfrac{{\rm{W}}}{2}\) trong thời gian \({t_0}\):
\({{\rm{W}}_L} = \dfrac{{{{\rm{W}}_{C\max }}}}{2} = \dfrac{{{{\rm{W}}_{LC}}}}{2} \Rightarrow {{\rm{W}}_C} = \dfrac{{{{\rm{W}}_{LC}}}}{2} \Leftrightarrow \dfrac{{C{u^2}}}{2} = \dfrac{1}{2}\dfrac{{CU_0^2}}{2} \Rightarrow u = \pm \dfrac{{{U_0}}}{{\sqrt 2 }}\)
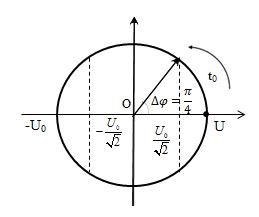
\( \Rightarrow {t_0} = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{\pi }{4}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{T}{8} \Rightarrow T = 8{t_0}\)
=> Chu kì dao động của mạch \(T{\rm{ }} = {\rm{ }}8{t_0}\)
Hướng dẫn giải:
+ Sử dụng vòng tròn lượng giác và công thức tính thời gian: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega }\) ( \(\Delta \varphi \) là góc quét được trong thời gian \(\Delta t\))
+ Sử dụng biểu thức tính năng lượng điện từ:
Câu hỏi khác
- Bài tập mạch dao động LC các đại lượng đặc trưng có lời giải MÔN LÝ lớp 12
- Bài tập năng lượng của mạch dao động LC có lời giải MÔN LÝ lớp 12
- Bài tập phương trình dao động mạch LC q,u,i có lời giải MÔN LÝ lớp 12
- Bài tập điện từ trường - sóng điện từ lý 12 có lời giải
- Bài tập các loại dao động lý 12 có lời giải
