Một mạch dao động LC lí tưởng gồm cuộn dây thuần cảm có \(L = 2mH\) và tụ điện có điện dung \(C = 2nF\). Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì dòng điện trong mạch có độ lớn \(\sqrt 2 A\). Lấy gốc thời gian là lúc dòng điện trong mạch có giá trị bằng một nửa giá trị cực đại và tụ đang phóng điện. Biểu thức của cường độ dòng điện trong mạch là:
Trả lời bởi giáo viên
Giả sử phương trình điện tích là : \(q = {Q_0}.\cos \left( {\omega t + \varphi } \right)\)
Phương trình cường độ dòng điện là : \(i = q' = - \omega .{Q_0}.\sin \left( {\omega t + \varphi } \right) = {I_0}.\cos \left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\)
Gốc thời gian là lúc tụ đang phóng điện tức là q đang giảm, ta có hình vẽ:
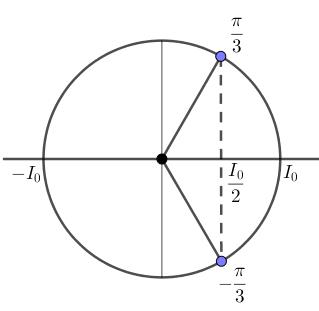
+ Vì q đang giảm nên I đang tăng => pha ban đầu của dòng điện \({\varphi _i} = - \dfrac{\pi }{3}\)
=> Phương trình của I là : \(i = {I_0}.\cos \left( {\omega t - \dfrac{\pi }{3}} \right)\)
+ Với tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {{{2.10}^{ - 3}}{{.2.10}^{ - 9}}} }} = {5.10^5}rad/s\)
+ Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì năng lượng từ trường cũng bằng một nửa năng lượng từ trường cực đại nên :
\(\begin{array}{*{20}{l}}{\dfrac{1}{2}L.{i^2} = \dfrac{1}{2}.\dfrac{1}{2}.L.I_0^2}\\{ = > I_0^2 = 2{i^2} = 2.{{\sqrt 2 }^2} = 4 = > {I_0} = 2A}\end{array}\)
Vậy phương trình của dòng điện i là: \(i = 2.\cos \left( {{{5.10}^5}t - \dfrac{\pi }{3}} \right)A\)
Hướng dẫn giải:
+ Vận dụng phương trình điện tích q => phương trình dòng điện
+ Sử dụng biểu thức tính tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }}\)
+ Vận dụng biểu thức tính năng lượng điện từ: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d}\)
+ Viết phương trình cường độ dòng điện trong mạch.