Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm \(5\mu H\) và tụ điện có điện dung \(5\mu F\). Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là:
Trả lời bởi giáo viên
Biểu diễn trên đường tròn lượng giác ta có:
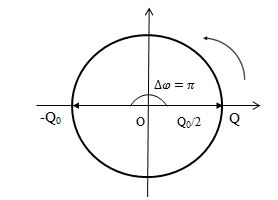
Theo bài ra ta tính được: \(T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{5.10}^{ - 6}}{{.5.10}^{ - 6}}} = \pi {.10^{ - 5}}s\)
→ Thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là :
\(\Delta t = \dfrac{{\Delta \varphi }}{\omega } = \pi .\dfrac{T}{{2\pi }} = \dfrac{T}{2} = \dfrac{{\pi {{.10}^{ - 5}}}}{2} = 5\pi {.10^{ - 6}}s\)
Hướng dẫn giải:
+ Sử dụng công thức tính chu kì của mạch dao động: \(T = \dfrac{1}{{2\pi \sqrt {LC} }}\)
+ Sử dụng vòng tròn lượng giác và công thức tính thời gian: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega }\) (\(\Delta \varphi \) là góc quét được trong thời gian \(\Delta t\))