Câu hỏi:
2 năm trước
Trong mạch dao động LC, tụ C được cấp năng lượng \({W_0} = {10^{ - 6}}J\) từ nguồn điện không đổi có suất điện động \(E = 4V\). Sau đó tụ phóng điện qua cuộn dây, cứ sau khoảng thời gian \(\Delta t = {10^{ - 6}}s\) thì năng lượng trong tụ điện và trong cuộn cảm lại bằng nhau. Cường độ cực đại trong cuộn dây là:
Trả lời bởi giáo viên
Đáp án đúng: d
Năng lượng điện từ: \({{\rm{W}}_0} = \dfrac{{CU_0^2}}{2} = \dfrac{{C{E^2}}}{2} \Rightarrow C = \dfrac{{2{{\rm{W}}_0}}}{{{E^2}}} = {1,25.10^{ - 7}}F\)
\({{\rm{W}}_{LC}} = {{\rm{W}}_L} + {{\rm{W}}_C} \Leftrightarrow {{\rm{W}}_{LC}} = 2{{\rm{W}}_C} \Leftrightarrow \dfrac{{CU_0^2}}{2} = 2.\dfrac{{C{u^2}}}{2} \Rightarrow u = \pm \dfrac{{{U_0}}}{{\sqrt 2 }}\)
Khi điện áp giữa hai đầu tụ điện \(u = \pm \dfrac{{{U_0}}}{{\sqrt 2 }}\) thì năng lượng điện trường bằng năng lượng từ trường.
Biểu diễn trên đường tròn lượng giác:
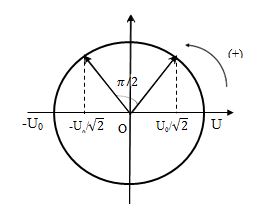
Góc quét được: \(\alpha = \dfrac{\pi }{2} \Rightarrow \Delta t = \dfrac{{\Delta \varphi }}{\omega } = \Delta \varphi .\dfrac{T}{{2\pi }} = \dfrac{\pi }{2}.\dfrac{T}{{2\pi }} = \dfrac{T}{4}\)
Cứ sau khoảng thời gian T/4 thì năng lượng điện trường lại bằng năng lượng từ trường
\( \Rightarrow \dfrac{T}{4} = {10^6}s \Rightarrow T = {4.10^{ - 6}}s = 2\pi \sqrt {LC} \Rightarrow L = \dfrac{{{T^2}}}{{4{\pi ^2}C}} = {3,24.10^{ - 6}}H\)
Từ công thức năng lượng: \(\dfrac{1}{2}LI_0^2 = {{\rm{W}}_0} \Rightarrow {I_0} = \sqrt {\dfrac{{2{W_0}}}{L}} = 0,785A\)
Hướng dẫn giải:
+ Sử dụng lí thuyết về năng lượng dao động điện từ: \(W = {W_L} + {W_C}\)
+ Sử dụng vòng tròn lượng giác
Câu hỏi khác
- Bài tập mạch dao động LC các đại lượng đặc trưng có lời giải MÔN LÝ lớp 12
- Bài tập năng lượng của mạch dao động LC có lời giải MÔN LÝ lớp 12
- Bài tập phương trình dao động mạch LC q,u,i có lời giải MÔN LÝ lớp 12
- Bài tập điện từ trường - sóng điện từ lý 12 có lời giải
- Bài tập các loại dao động lý 12 có lời giải
