Bài tập mạch xoay chiều RLC - có L thay đổi

Ta có L thay đổi để U_L max, khi đó: \({U_{Lm{\rm{ax}}}} = \dfrac{{U_R^2 + U_C^2}}{{{U_C}}} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{R}\)

\(\left\{ \begin{array}{l}{U_{RC}} \bot {U_{AB}}\\U_{L\max }^2 = {U^2} + U_{RC}^2 = {U^2} + U_R^2 + U_C^2\\U_{L\max }^{}.{U_R} = U.{U_{RC}}\\\dfrac{1}{{U_R^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RC}^2}}\end{array} \right.\)

=> Các phương án:

+ A, B, C – đúng

+ D – sai vì: \(\dfrac{1}{{U_R^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RL}^2}}\)

Ta có: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)

L biến thiên để U_L max khi đó: \({Z_L} = \dfrac{{{R^2} + Z_C^2}}{{{Z_C}}}\)

\( \to {Z_L} = \dfrac{{{{80}^2} + {{100}^2}}}{{100}} = 164\Omega \)

Mặt khác: \({Z_L} = \omega L \to L = \dfrac{{{Z_L}}}{\omega } = \dfrac{{164}}{{100\pi }} = \dfrac{{1,64}}{\pi }(H)\)

L biến thiên để \({U_L}\) max khi đó: \({Z_L} = \dfrac{{{R^2} + Z_C^2}}{{{Z_C}}}\) và \({U_{Lm{\rm{ax}}}} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{R}\)

\( \to {Z_L} = \dfrac{{{R^2} + Z_C^2}}{{{Z_C}}} = \dfrac{{{{30}^2} + {{40}^2}}}{{40}} = 62,5\Omega \)

\({U_{Lm{\rm{ax}}}} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{R} = \dfrac{{120\sqrt {{{30}^2} + {{40}^2}} }}{{30}} = 300(V)\)

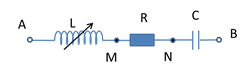
L biến thiên để \({U_L}\) max, khi đó:

\(\begin{array}{l}U_{L\max }^2 = {U^2} + U_{RC}^2 = {U^2} + U_{MB}^2 = {100^2} + {240^2}\\ \to {U_L} = 260(V)\end{array}\)

Thay đổi L đến khi \(L = {L_0}\) thì cường độ dòng điện trong mạch đạt cực đại khi đó, xảy ra cộng hưởng điện

\({Z_L} = {Z_C} \leftrightarrow \omega {L_0} = \dfrac{1}{{\omega C}} \to {L_0} = \dfrac{1}{{{\omega ^2}C}}\)

Thay đổi L đến khi \(L = {L_0}\) thì tổng trở của mạch cực tiểu \(\left( {{Z_{\min }}} \right)\) khi đó, xảy ra cộng hưởng điện

\({Z_L} = {Z_C} \leftrightarrow \omega {L_0} = \dfrac{1}{{\omega C}} \to {L_0} = \dfrac{1}{{{\omega ^2}C}}\)

Thay đổi L đến khi \(L = {L_0}\) thì điện áp và cường độ dòng điện trong mạch cùng pha với nhau khi đó, xảy ra cộng hưởng điện

\({Z_L} = {Z_C} \leftrightarrow \omega {L_0} = \dfrac{1}{{\omega C}} \to {L_0} = \dfrac{1}{{{\omega ^2}C}}\)

\(L\) thay đổi để \({P_{max}}\) , khi đó, mạch xảy ra cộng hưởng

\({Z_L} = {Z_C}\) và  \(\left\{ \begin{array}{l}{Z_{\min }} = R\\{I_{{\rm{max}}}} = \dfrac{U}{R}\\{U_{{R_{max}}}} = U\\{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\end{array} \right.\)

\(L\) thay đổi để \({U_{{R_{max}}}}\) , khi đó, mạch xảy ra cộng hưởng

\({Z_L} = {Z_C}\) và  \(\left\{ \begin{array}{l}{Z_{\min }} = R\\{I_{{\rm{max}}}} = \dfrac{U}{R}\\{U_{{R_{max}}}} = U\\{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\end{array} \right.\)

L thay đổi để \({U_{Cmax}}\), khi đó mạch xảy ra cộng hưởng điện

\({Z_L} = {Z_C}\) và  \(\left\{ \begin{array}{l}{Z_{\min }} = R\\{I_{{\rm{max}}}} = \dfrac{U}{R}\\{U_{{R_{max}}}} = U\\{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\end{array} \right.\)

Ta có, điện áp hiệu dụng trên hai đầu cuộn cảm: \({U_L} = I.{Z_L} = \dfrac{U}{R}{Z_L} = \dfrac{U}{R}{Z_C}\) (vì \({Z_L} = {Z_C}\))

\(L\) thay đổi để mạch xảy ra cộng hưởng khi đó: \({Z_L} = {Z_C}\) và \(\left\{ \begin{array}{l}{Z_{\min }} = R\\{I_{{\rm{max}}}} = \dfrac{U}{R}\\{U_{{R_{max}}}} = U\\{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\end{array} \right.\)

A – sai vì: \({Z_{\min }} = R\)

B – sai vì: \({I_{max}} = \dfrac{U}{R}\)

C - đúng

D - sai vì khi đó u và i cùng pha với nhau \(\left( {{\varphi _u} = {\varphi _i}} \right)\)

\(L\) thay đổi để \({I_{max}}\), khi đó: \({I_{{\rm{max}}}} = \dfrac{U}{R} = \dfrac{{\dfrac{{120\sqrt 2 }}{{\sqrt 2 }}}}{{60}} = 2(A)\)

- Ta có:  L biến thiên để \({U_{Rmax}}\) khi mạch xảy ra hiện tượng cộng hưởng điện: \({Z_L} = {Z_C}\)

+ Cường độ dòng điện cực đại khi đó: \({I_0} = \dfrac{{{U_0}}}{R} = \dfrac{{160}}{{80}} = 2(A)\)

+ Mạch xảy cộng hưởng => u, i cùng pha \( \to {\varphi _i} = {\varphi _u} = \dfrac{\pi }{3}\left( {rad} \right)\)

- Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{200.10}^{ - 6}}}}{\pi }}} = 50\Omega \)

- Hiệu điện thế cực đại giữa hai đầu tụ điện: \({U_{0C}} = {I_0}{Z_C} = 2.50 = 100(V)\)

- Mặt khác, ta có \({u_C}\) chậm pha hơn \(i\) một góc \(\dfrac{\pi }{2}(ra{\rm{d}})\)

\( \to {\varphi _{{u_C}}} = {\varphi _i} - \dfrac{\pi }{2} = \dfrac{\pi }{3} - \dfrac{\pi }{2} =  - \dfrac{\pi }{6}\left( {rad} \right)\)

=> Biểu thức điện áp giữa hai đầu cuộn cảm: \({u_C} = 100c{\rm{os}}\left( {100\pi t - \dfrac{\pi }{6}} \right)V\)

Ta có:

+ Khi \(L = {L_1}\): cường độ dòng điện qua mạch cực đại

=> Khi đó mạch cộng hưởng: \({Z_C} = {Z_{{L_1}}}\)(1)

+ Khi \(L = 2{L_1} \to {Z_L} = 2{Z_{{L_1}}}\): thì \({U_L}max\) , khi đó ta có:

\({Z_L} = \dfrac{{{R^2} + Z_C^2}}{{{Z_C}}} = 2{Z_{{L_1}}}\) (2)

Từ (1) và (2): \( \to \dfrac{{{R^2} + {Z_C}^2}}{{{Z_C}}} = 2{Z_{{L_1}}} = 2{Z_C} \to R = {Z_L} = {Z_{{C_1}}} = 40\Omega \)

Mặt khác: \({Z_{{L_1}}} = \omega {L_1} \to \omega  = \dfrac{{{Z_{{L_1}}}}}{{{L_1}}} = \dfrac{{40}}{{\dfrac{1}{{2\pi }}}} = 80\pi \left( {rad/s} \right)\)

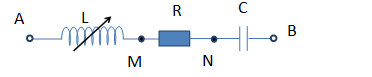
L thay đổi để U_RL max khi đó: \({Z_L} = \dfrac{{{Z_C}}}{2} = \dfrac{R}{2} = \dfrac{{80}}{2} = 40\Omega \)

Mặt khác: \({Z_L} = \omega L \to L = \dfrac{{{Z_L}}}{\omega } = \dfrac{{{Z_L}}}{{2\pi .f}} = \dfrac{{40}}{{2\pi 50}} = \dfrac{2}{{5\pi }}(H)\)

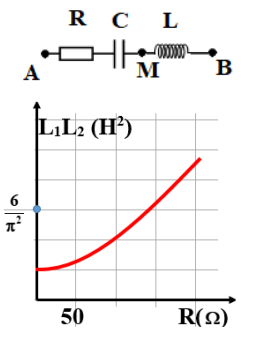
+ L thay đổi để U_AM = \(\dfrac{U}{{\sqrt {{R^2} + Z_{LC}^2} }}.\sqrt {{R^2} + Z_C^2} \) không phụ thuộc vào R nên

\({R^2} + Z_C^2 = {R^2} + Z_{LC}^2 \to Z_C^2 = {({Z_L} - {Z_C})^2} \Rightarrow {Z_{L1}} = 2{Z_C}\) (1)

+ L thay đổi để U_L max nên \({Z_{L2}} = \dfrac{{{R^2} + Z_C^2}}{{{Z_C}}}\) (2)

+ Nhìn vào đồ thị ta thấy khi R = 100Ω thì \({L_1}{L_2} = \dfrac{4}{{{\pi ^2}}} \Rightarrow {Z_{L1}}{Z_{L2}} = \dfrac{4}{{{\pi ^2}}}.{\omega ^2} = 40000\) (3)

Từ (1), (2), (3) ta được Z_C= 100Ω

Để công suất tiêu tụ của mạch cực đại thì Z_L = Z_C = 100Ω \( \Rightarrow L = \dfrac{1}{\pi }(H)\)

Khi \({Z_1} = {Z_2}\)

\({R^2} + {({Z_{L1}} - {Z_C})^2} = {R^2} + {({Z_{L2}} - {Z_C})^2} \to \left| {{Z_{L1}} - {Z_C}} \right| = \left| {{Z_{L2}} - {Z_C}} \right|\)

Với \({Z_{{L_2}}} > {Z_{{L_1}}}\) \( \to {Z_{L1}} + {Z_{L2}} = 2{Z_C}\)

Ta có:

L thay đổi \({P_{max}}\) khi \({Z_L} = {Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{{{100.125.10}^{ - 6}}}} = 80\Omega \)

Mặt khác: \(P = \dfrac{{{U^2}}}{{{Z^2}}}R = \dfrac{{{U^2}}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}R\)

Khi giảm L để cảm kháng giảm từ \(60\Omega \) đến \(20\Omega \)thì tổng trở của mạch tăng dần => P giảm

=> Công suất tiêu thụ trên mạch giảm dần theo sự giảm của cảm kháng

Ta có:

Khi \(L{\rm{ }} = {\rm{ }}{L_1}\) thì \({U_{AM1}} = {\rm{ }}{U_{R1}} = {\rm{ }}U\)

Khi L = L₂ thì

\({\varphi _1} + {\varphi _2} = \dfrac{\pi }{2} \to \tan {\varphi _1}\tan {\varphi _2} =  - 1 \to \dfrac{{{Z_{L1}} - {Z_C}}}{R}.\dfrac{{{Z_{L2}} - {Z_C}}}{R} =  - 1{\rm{       }}(1)\)

Mặt khác: ta có

\(\begin{array}{l}\dfrac{{{U_{R1}}}}{{{U_{R2}}}} = \dfrac{1}{{\sqrt 3 }} \to {I_2} = \sqrt 3 {I_1} \to {Z_1} = \sqrt 3 {Z_2}\\ \leftrightarrow \sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_C}} \right)}^2}}  = \sqrt 3 \sqrt {{R^2} + {{\left( {{Z_{L2}} - {Z_C}} \right)}^2}} \\ \leftrightarrow {\left( {{Z_{L1}} - {Z_C}} \right)^2} - 2{R^2} - 3{\left( {{Z_{L2}} - {Z_C}} \right)^2} = 0{\rm{      (2)}}\end{array}\)

Chia cả hai vế của (2) cho \(\left( {{Z_{L2}} - {\rm{ }}{Z_C}} \right)\) kết hợp với (1), ta được: \(\dfrac{{{{\left( {{Z_{L1}} - {Z_C}} \right)}^2}}}{{{{\left( {{Z_{L2}} - {Z_C}} \right)}^2}}} + 2\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} - 3 = 0{\rm{ }} \to \left[ \begin{array}{l}\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} = 1(Loai)\\\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} =  - 3\end{array} \right.\)

Với \(\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} =  - 3 \to  - \dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{3} = \left( {{Z_{L2}} - {Z_C}} \right)\)

Thay vào (1) =>\({\left( {{Z_{L1}} - {Z_C}} \right)^2} = 3{R^2}\)

Hệ số công suất của mạch khi \(L = {L_1}\) : \({\rm{cos}}{\varphi _1} = \dfrac{R}{{{Z_1}}} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_C}} \right)}^2}} }} = \dfrac{R}{{\sqrt {{R^2} + 3{R^2}} }} = \dfrac{R}{{2R}} = \dfrac{1}{2}\)

- L biến thiên để \({U_{Rmax}},{\rm{ }}{U_{Cmax}}\)  <=> cộng hưởng điện

Khi đó: \(\left\{ \begin{array}{l}{U_{{R_{{\rm{max}}}}}} = U\\{U_{{C_{{\rm{max}}}}}} = \dfrac{U}{R}{Z_C}\end{array} \right.\)

- L biến thiên để \({U_{Lmax}}\)

Khi đó: \({U_{{L_{{\rm{max}}}}}} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{R}\)

Theo đề bài, ta có:

\(\begin{array}{l}{U_{{L_{{\rm{max}}}}}} = \sqrt {10} {U_{{R_{{\rm{max}}}}}} = \sqrt {10} U\\ \to \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{R} = \sqrt {10} U \to \sqrt {{R^2} + Z_C^2}  = \sqrt {10} R\\ \to {R^2} + Z_C^2 = 10{R^2}\\ \to Z_C^2 = 9{R^2} \to {Z_C} = 3R\end{array}\)

=> Tỉ số: \(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{{\dfrac{U}{R}{Z_C}}}{{\sqrt {10} U}} = \dfrac{{{Z_C}}}{{\sqrt {10} R}} = \dfrac{{3R}}{{\sqrt {10} R}} = \dfrac{3}{{\sqrt {10} }}\)