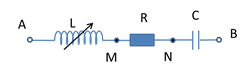
Đặt điện áp \(u = 220\sqrt 2 {\rm{cos}}\omega {\rm{t (V)}}\) (với \(\omega \) không đổi) vào hai đầu đoạn mạch AB gồm đoạn mạch AM  nối tiếp đoạn mạch MB. Đoạn mạch AM có điện trở thuần R, đoạn mạch MB có cuộn cảm thuần có độ tự cảm L thay đổi được và tụ điện có điện dung C mắc nối tiếp. Điện áp hiệu dụng ở hai đầu đoạn mạch AM và độ lớn góc lệch pha của cường độ dòng điện so với điện áp u khi \(L{\rm{ }} = {\rm{ }}{L_1}\) là \(U\) và \({\varphi _1}\), còn khi \(L{\rm{ }} = {\rm{ }}{L_2}\) thì tương ứng là \(\sqrt 3 U\) và \({\varphi _2}\). Biết \({\varphi _1} + {\varphi _2} = {90^0}\). Hệ số công suất của mạch khi \(L{\rm{ }} = {\rm{ }}{L_1}\) là:

Ta có:

Khi \(L{\rm{ }} = {\rm{ }}{L_1}\) thì \({U_{AM1}} = {\rm{ }}{U_{R1}} = {\rm{ }}U\)

Khi L = L₂ thì

\({\varphi _1} + {\varphi _2} = \dfrac{\pi }{2} \to \tan {\varphi _1}\tan {\varphi _2} =  - 1 \to \dfrac{{{Z_{L1}} - {Z_C}}}{R}.\dfrac{{{Z_{L2}} - {Z_C}}}{R} =  - 1{\rm{       }}(1)\)

Mặt khác: ta có

\(\begin{array}{l}\dfrac{{{U_{R1}}}}{{{U_{R2}}}} = \dfrac{1}{{\sqrt 3 }} \to {I_2} = \sqrt 3 {I_1} \to {Z_1} = \sqrt 3 {Z_2}\\ \leftrightarrow \sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_C}} \right)}^2}}  = \sqrt 3 \sqrt {{R^2} + {{\left( {{Z_{L2}} - {Z_C}} \right)}^2}} \\ \leftrightarrow {\left( {{Z_{L1}} - {Z_C}} \right)^2} - 2{R^2} - 3{\left( {{Z_{L2}} - {Z_C}} \right)^2} = 0{\rm{      (2)}}\end{array}\)

Chia cả hai vế của (2) cho \(\left( {{Z_{L2}} - {\rm{ }}{Z_C}} \right)\) kết hợp với (1), ta được: \(\dfrac{{{{\left( {{Z_{L1}} - {Z_C}} \right)}^2}}}{{{{\left( {{Z_{L2}} - {Z_C}} \right)}^2}}} + 2\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} - 3 = 0{\rm{ }} \to \left[ \begin{array}{l}\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} = 1(Loai)\\\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} =  - 3\end{array} \right.\)

Với \(\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} =  - 3 \to  - \dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{3} = \left( {{Z_{L2}} - {Z_C}} \right)\)

Thay vào (1) =>\({\left( {{Z_{L1}} - {Z_C}} \right)^2} = 3{R^2}\)

Hệ số công suất của mạch khi \(L = {L_1}\) : \({\rm{cos}}{\varphi _1} = \dfrac{R}{{{Z_1}}} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_C}} \right)}^2}} }} = \dfrac{R}{{\sqrt {{R^2} + 3{R^2}} }} = \dfrac{R}{{2R}} = \dfrac{1}{2}\)