Mỗi giây dòng điện đổi chiều bao nhiêu lần? Biết dòng điện xoay chiều qua mạch có chu kì dao động là T.
Ta có, trong mỗi giây dòng điện đổi chiều \(2f\) lần
Từ thông qua khung dây có biểu thức: \(\Phi = {\Phi _0}\cos 50\pi t\). Trong 1s dòng điện trong khung dây đổi chiều:
Ta có, trong mỗi giây dòng điện đổi chiều \(2f\) lần
Từ biểu thức: \(\Phi = {\Phi _0}\cos 50\pi t\), ta có \(\omega = 50\pi \to f = \dfrac{\omega }{{2\pi }} = \dfrac{{50\pi }}{{2\pi }} = 25(H{\rm{z}})\)
=> Trong 1s dòng điện đổi chiều \(2.25 = 50\) lần
Dòng điện xoay chiều qua một đoạn mạch có biểu thức \(i = {I_0}{\rm{cos}}\left( {80\pi t + \dfrac{\pi }{2}} \right)A\). Trong 2,5s dòng điện đổi chiều bao nhiêu lần?
Từ biểu thức cường độ dòng điện: \(i = {I_0}{\rm{cos}}\left( {80\pi t + \dfrac{\pi }{2}} \right)A\)
Ta có: tần số \(f = \dfrac{\omega }{{2\pi }} = \dfrac{{80\pi }}{{2\pi }} = 40(H{\rm{z}})\)
Ta có: Nếu pha ban đầu \({\varphi _i} = \dfrac{\pi }{2}\) hoặc \({\varphi _i} = - \dfrac{\pi }{2}\)thì chỉ giây đầu tiên đổi chiều \(2f - 1\) lần
=> Trong 2,5s , dòng điện đổi chiều: \(2,5(2f) - 1 = 2,5.(2.40) - 1 = 199\) lần
Tại thời điểm t, điện áp \(u = 200\sqrt 2 {\rm{cos}}\left( {100\pi t - \dfrac{\pi }{2}} \right)\) (trong đó u tính bằng V, t tính bằng s) có giá trị \(100\sqrt 2 \) và đang tăng. Sau thời điểm đó \(\dfrac{7}{{600}}s\), điện áp này có giá trị là:
Góc quay từ t đến \(\dfrac{7}{{600}}s\) : \(\Delta \varphi = \omega \Delta t = 100\pi \dfrac{7}{{600}} = \dfrac{{7\pi }}{6}(ra{\rm{d}})\)
Xác định các điểm trên vòng tròn lượng giác, ta được:
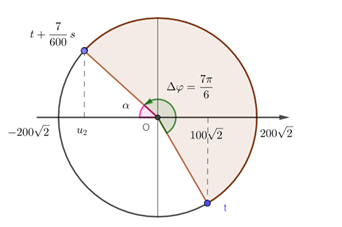
Từ vòng tròn ta có:
Tại thời điểm: \(t + \dfrac{7}{{600}}s\): điện áp có giá trị: \({u_2} = - {U_0}cos\alpha \)
Ta có: \(\alpha = \dfrac{\pi }{6}\left( {rad} \right) \to {u_2} = - {U_0}cos\dfrac{\pi }{6} = - 200\sqrt 2 cos\dfrac{\pi }{6} = - 100\sqrt 6 V\)
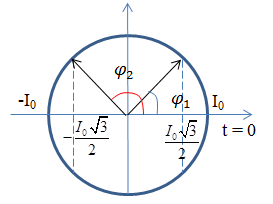
Vào cùng một thời điểm nào đó, hai dòng điện xoay chiều \({i_1} = {I_0}cos(\omega t + {\varphi _1})\) và \({i_2} = {I_0}cos(\omega t + {\varphi _2})\)đều có cùng giá trị tức thời là \(\dfrac{{{I_0}\sqrt 3 }}{2}\) nhưng một dòng điện đang giảm, còn một dòng điện đang tăng. Hai dòng điện này lệch pha nhau một góc bằng:
Giả sử tại thời điểm đó \({i_1} = \dfrac{{{I_0}\sqrt 3 }}{2}\) và đang tăng, \({i_2} = \dfrac{{{I_0}\sqrt 3 }}{2}\) và đang giảm
Vẽ vòng tròn lượng giác, ta được:
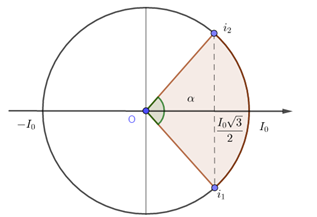
Từ vòng tròn lượng giác ta có:
\(cos\dfrac{\alpha }{2} = \dfrac{{\sqrt 3 }}{2} \to \dfrac{\alpha }{2} = \dfrac{\pi }{6} \to \alpha = \dfrac{\pi }{3}\left( {rad} \right)\)
Độ lệch pha giữa hai dòng điện này là: \(\Delta \varphi = \alpha = \dfrac{\pi }{3}\)
Dòng điện xoay chiều qua một đoạn mạch có biểu thức \(i = {I_0}{\rm{cos}}\left( {120\pi t - \dfrac{\pi }{3}} \right)A\) thời điểm thứ \(2019\) cường độ dồng điện tức thời có độ lớn bằng cường độ hiệu dụng là:
Ta có:
+ Chu kì dao động : \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{120\pi }} = \dfrac{1}{{60}}s\)
+ \({t_{2019}} = {\rm{ }}{t_{2016}} + {\rm{ }}{t_3}\)
Trong 1 chu kì, cường độ dòng điện có độ lớn bằng cường độ hiệu dụng 4 lần
\( \to {t_{2016}} = \dfrac{{2016}}{4}T = 504T\)
Tại \(t{\rm{ }} = {\rm{ }}0\) : \(i = {I_0}{\rm{cos}}\left( { - \dfrac{\pi }{3}} \right) = \dfrac{{{I_0}}}{2}\)
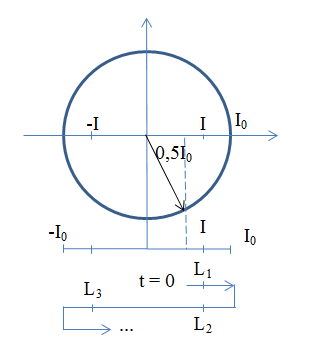
\(\begin{array}{l}{t_3} = \dfrac{T}{6} + \dfrac{T}{4} + \dfrac{T}{8} = \dfrac{{13T}}{{24}}\\ \to {t_{2019}} = {t_{2016}} + {t_3} = 504T + \dfrac{{13T}}{{24}} = \dfrac{{12109}}{{24}}T = \dfrac{{12109}}{{24}}.\dfrac{1}{{60}} = \dfrac{{12109}}{{1440}}(s)\end{array}\)
Điện áp tức thời giữa hai đầu đoạn mạch có biểu thức: \(u = 240\sin \left( {100\pi t} \right)V\). Thời điểm gần nhất sau đó để điện áp tức thời đạt giá trị \(120\sqrt 3 V\) kể từ thời điểm ban đầu là:
Chu kì dao động : \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{100\pi }} = 0,02s\)
Tại t = 0: \(u = 240\sin 0 = 0(V)\)
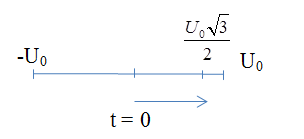
Thời điểm gần nhất sau đó để điện áp tức thời đạt giá trị \(120\sqrt 3 = \dfrac{{{U_0}\sqrt 3 }}{2}\) kể từ thời điểm ban đầu là: \(t = \dfrac{T}{6} = \dfrac{{0,02}}{6} = \dfrac{1}{{300}}s\)
Dòng điện chạy qua một đoạn mạch có biểu thức \(i = {I_0}{\rm{cos}}\left( {100\pi t} \right)A\). Trong khoảng thời gian từ \(0\) đến \(0,01s\) cường độ dòng điện tức thời trong có độ lớn bằng \(\dfrac{{{I_0}\sqrt 3 }}{2}\) vào những thời điểm:
Ta có, từ thời điểm \(0 - 0,01s\) thì góc quay được là:
\(\Delta \varphi = \omega \Delta t = 100\pi .0,01 = \pi (ra{\rm{d}})\)
Tại t = 0: \(i = {I_0}{\rm{cos0}} = {I_0}(A)\)
Từ vòng tròn lượng giác ta có:
+ \({\varphi _1} = \omega {t_1} = \dfrac{\pi }{6} \to {t_1} = \dfrac{1}{{600}}s\)
+ \({\varphi _2} = \omega {t_2} = \dfrac{{5\pi }}{6} \to {t_2} = \dfrac{1}{{120}}s\)
Dòng điện xoay chiều \(i = 2sin\left( {100\pi t + \dfrac{\pi }{3}} \right){\rm{ }}A\) qua một dây dẫn. Điện lượng chạy qua tiết diện dây trong khoảng thời gian từ \(0\) đến \(0,1s\) là:
Ta có, điện lượng chạy qua tiết diện dây:
\(\Delta q = \int\limits_{{t_1}}^{{t_2}} {i{\rm{d}}t} = \int\limits_0^{0,1} {2sin(100\pi t + \dfrac{\pi }{3}){\rm{d}}t} = \dfrac{{ - 2}}{{100\pi }}{\rm{cos}}\left( {{\rm{100}}\pi {\rm{t + }}\dfrac{\pi }{3}} \right)\left| {_0^{0,1}} \right. = \dfrac{{ - 2}}{{100\pi }}\left( {\dfrac{1}{2} - \dfrac{1}{2}} \right) = 0\)
Dòng điện xoay chiều hình sin chạy qua một đoạn mạch có biểu thức cường độ là \(i = {I_0}{\rm{cos}}\left( {\omega t} \right)A\) , \({I_0} > 0\). Tính từ lúc \(t = 0\left( s \right)\), điện lượng chuyển qua tiết diện phẳng của dây dẫn của đoạn mạch đó trong thời gian bằng nửa chu kì của dòng điện là:
Ta có, điện lượng chạy qua tiết diện dây:
\(\Delta q = \int\limits_{{t_1}}^{{t_2}} {i{\rm{d}}t} = \int\limits_0^{\dfrac{T}{2}} {{I_0}{\rm{cos}}\left( {\omega t} \right){\rm{d}}t} = \dfrac{{{I_0}}}{\omega }{\rm{sin}}\left( {\omega t} \right)\left| {_0^{\dfrac{T}{2}}} \right. = \dfrac{{{I_0}}}{\omega }\left( {0 - 0} \right) = 0\)
Một chiếc đèn neon đặt dưới một điện áp xoay chiều \(120V - 50Hz\). Nó chỉ sáng lên khi điện áp tức thời giữa hai đầu bóng đèn lớn hơn \(120V\). Thời gian bóng đèn sáng trong một chu kì là bao nhiêu?
Ta có:
+ Hiệu điện thế cực đại: \({U_0} = 120\sqrt 2 (V)\)
+ Tần số góc: \(\omega = 2\pi f = 2\pi .50 = 100\pi (ra{\rm{d}}/s)\)
+ Vẽ trên vòng tròn lượng giác, ta được:
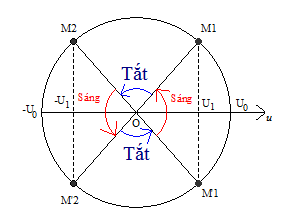
Biết đèn chỉ sáng lên khi \(u \ge {U_1}\)
Ta có:
+ \(c{\rm{os}}\Delta \varphi = \dfrac{{{U_1}}}{{{U_0}}} = \dfrac{{120}}{{120\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }} \to \Delta \varphi = \dfrac{\pi }{4}\)
Thời gian đèn sáng trong 1 chu kì: \(\Delta t = \dfrac{{4\Delta \varphi }}{\omega } = \dfrac{{4\dfrac{\pi }{4}}}{{100\pi }} = \dfrac{1}{{100}} = 0,01s\)
Đặt điện áp xoay chiều có giá trị hiệu dụng \(155,56V\), tần số \(f = 50Hz\) vào hai đầu một bóng đèn huỳnh quang. Biết đèn chỉ sáng lên khi điện áp đặt vào đèn không nhỏ hơn \(120V\). Thời gian đèn sáng trong mỗi giây là:
Ta có:
+ Hiệu điện thế cực đại: \({U_0} =155,56\sqrt 2 (V)\)
+ Tần số góc: \(\omega = 2\pi f = 2\pi .50 = 100\pi (ra{\rm{d}}/s)\)
+ Vẽ trên vòng tròn lượng giác, ta được:
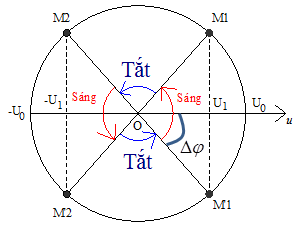
Biết đèn chỉ sáng lên khi \(u \ge {\rm{ }}{U_1}\)
Ta có:
+ \(c{\rm{os}}\Delta \varphi = \dfrac{{{U_1}}}{{{U_0}}} = \dfrac{{120}}{{155,56.\sqrt 2 }} \approx 0,54 \to \Delta \varphi \approx {60^0} = \dfrac{\pi }{3}\)
Thời gian đèn sáng trong 1 chu kì: \(\Delta t = \dfrac{{4\Delta \varphi }}{\omega } = \dfrac{{4\dfrac{\pi }{3}}}{{100\pi }} = \dfrac{1}{{75}}s\)
Ta có:
+ Chu kì \(T = \dfrac{1}{f} = \dfrac{1}{{50}}s\)
+ \(1{\rm{s}} = 50T\)
=> Thời gian đèn sáng trong 1s là: \(t = \Delta t.50 = 50.\dfrac{1}{{75}} = \dfrac{2}{3}s\)
Đặt điện áp xoay chiều có giá trị hiệu dụng \(U = 120V\), tần số \(f{\rm{ }} = {\rm{ }}60Hz\) vào hai đầu một bóng đèn huỳnh quang. Biết đèn chỉ sáng lên khi điện áp đặt vào đèn không nhỏ hơn \(60\sqrt 6 V\). Tỉ số thời gian đèn sáng và đèn tắt trong \(30\) phút là:
Ta có:
+ Hiệu điện thế cực đại: \({U_0} = 120\sqrt 2 (V)\)
+ Tần số góc: \(\omega = 2\pi f = 2\pi .60 = 120\pi (ra{\rm{d}}/s)\)
+ Vẽ trên vòng tròn lượng giác, ta được:
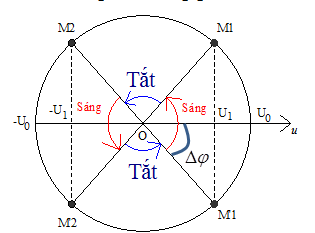
Biết đèn chỉ sáng lên khi u ≥ U1
Ta có:
+ \(c{\rm{os}}\Delta \varphi = \dfrac{{{U_1}}}{{{U_0}}} = \dfrac{{60\sqrt 6 }}{{120\sqrt 2 }} = \dfrac{{\sqrt 3 }}{2} \to \Delta \varphi = \dfrac{\pi }{6}\)
Thời gian đèn sáng trong 1 chu kì: \(\Delta t = \dfrac{{4\Delta \varphi }}{\omega } = \dfrac{{4\dfrac{\pi }{6}}}{{120\pi }} = \dfrac{1}{{180}}s\)
Thời gian đèn tắt trong 1 chu kì: \(\Delta t' = T - \Delta t = \dfrac{1}{{60}} - \dfrac{1}{{180}} = \dfrac{1}{{90}}s\)
Ta có:
+ Chu kì \(T = \dfrac{1}{f} = \dfrac{1}{{60}}s\)
+ \(t = 30' = 30.60s = 108000T\)
=> Thời gian đèn sáng trong 30’ là: \({t_1} = t.\Delta t\)
Thời gian đèn tắt trong 30’ là: \({t_2} = t.\Delta t'\)
Tỉ số thời gian đèn sáng và đèn tắt trong 30 phút là: \(\dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{\dfrac{1}{{180}}}}{{\dfrac{1}{{90}}}} = \dfrac{1}{2}\)
Điện áp hai đầu bóng đèn có biểu thức \({\rm{u = 100}}\sqrt[]{2}{\rm{cos100}}\pi {\rm{t}}\). Đèn chỉ sáng khi \({\rm{u}} \ge {\rm{100 V}}\). Tính tỉ lệ thời gian đèn sáng - tối trong một chu kỳ?
Ta có VTLG:
Thời gian đèn tối tương ứng (1) đến (2) và (3) đến (4) trên VTLG.
Góc quét được trong thời gian đèn tối là: \({\alpha _T} = 2.\dfrac{\pi }{2} = \pi \)
Thời gian đèn sáng tương ứng (4) đến (1) và (2) đến (3) trên VTLG.
Góc quét được trong thời gian đèn sáng là: \({\alpha _S} = 2.\dfrac{\pi }{2} = \pi \)
Ta có: \({\alpha _S} = {\alpha _T} \Rightarrow {t_S} = {t_T} \Rightarrow \dfrac{{{t_S}}}{{{t_T}}} = 1\)
Cho dòng điện xoay chiều có cường độ i = 2cos(100πt)(A) chạy qua một đoạn mạch điện. Cứ mỗi giây, số lần cường độ dòng điện bằng 0 là
Chu kỳ của dòng điện: \(T = \dfrac{{2\pi }}{\omega }\) = 0,02s
Trong 1s = 50T có 100 lần cường độ dòng điện bằng 0
Dòng điện xoay chiều qua một đoạn mạch có chu kì là T (s) biểu thức cường độ là \(i = {I_0}\cos \left( {\omega t + \pi } \right)\left( A \right)\), t tính bằng s. Tính từ lúc \(t = 0\), điện lượng chuyển qua mạch trong \(\dfrac{T}{4}\)(s) đầu tiên là
Điện lượng chuyển qua mạch trong \(\dfrac{T}{4}\left( s \right)\) đầu tiên:
\(q = \int\limits_{t1}^{t2} {i.dt} = \int\limits_0^{\dfrac{T}{4}} {{I_0}\cos \left( {\omega t + \pi } \right).dt = \dfrac{{{I_0}}}{\omega }\sin \left( {\omega t + \pi } \right)\left| \begin{array}{l}\dfrac{T}{4}\\0\end{array} \right.} = - \dfrac{{{I_0}}}{\omega }\)
Dòng điện xoay chiều qua một đoạn mạch có tần số dao động là $f$. Mỗi giây dòng điện đổi chiều bao nhiêu lần?
Trong mỗi giây: Dòng điện đổi chiều $2f$ lần
Từ thông qua khung dây có biểu thức: \(\Phi = {\Phi _0}\cos 40\pi t\). Trong $1s$ dòng điện trong khung dây đổi chiều:
Ta có, trong mỗi giây dòng điện đổi chiều $2f$ lần
Từ biểu thức:
\(\Phi = {\Phi _0}\cos 40\pi t\),
ta có
$\omega = 40\pi \to f = \dfrac{\omega }{{2\pi }} = \dfrac{{40\pi }}{{2\pi }} = 20(H{\text{z}})$
=> Trong $1s$ dòng điện đổi chiều $2f = 2.20 = 40$ lần
Dòng điện xoay chiều qua một đoạn mạch có biểu thức $i = {I_0}{\text{cos}}\left( {120\pi t - \dfrac{\pi }{2}} \right)A$. Trong $2,5s$ dòng điện đổi chiều bao nhiêu lần?
Từ biểu thức cường độ dòng điện:
$i = {I_0}{\text{cos}}\left( {120\pi t - \dfrac{\pi }{2}} \right)A$
Ta có: tần số
$f = \dfrac{\omega }{{2\pi }} = \dfrac{{120\pi }}{{2\pi }} = 60(H{\text{z}})$
Ta có: Nếu pha ban đầu ${\varphi _i} = \dfrac{\pi }{2}$ hoặc ${\varphi _i} = - \dfrac{\pi }{2}$
thì chỉ giây đầu tiên đổi chiều 2f-1 lần
=> Trong 2,5s , dòng điện đổi chiều:
$2,5(2f) - 1 = 2,5.(2.60) - 1 = 299$ lần
Tại thời điểm t, điện áp $u = 200\sqrt 2 {\text{cos}}\left( {100\pi t - \dfrac{\pi }{2}} \right)$ (trong đó u tính bằng V, t tính bằng s) có giá trị $100\sqrt 2 $ và đang giảm. Sau thời điểm đó $\dfrac{1}{{300}}s$, điện áp này có giá trị là:
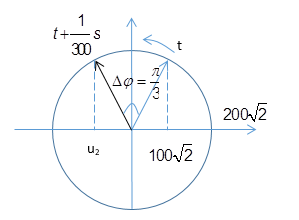
Xác định các điểm trên vòng tròn lượng giác, ta được:
Góc quay từ t đến $\dfrac{1}{{300}}s$ :
$\Delta \varphi = \omega \Delta t = 100\pi \dfrac{1}{{300}} = \dfrac{\pi }{3}(ra{\text{d}})$
Từ vòng tròn ta có:
Tại thời điểm $t + \dfrac{1}{{300}}s$ điện áp có giá trị: ${u_2} = - 100\sqrt 2 (V)$

