Công suất điện tiêu thụ của mạch điện xoay chiều - Hệ số công suất

Một đoạn mạch RLC mắc nối tiếp được mắc vào điện áp (\(U\) không đổi). Cường độ dòng điện hiệu dụng trong mạch đạt giá trị cực đại khi xảy ra hiện tượng cộng hưởng: \({\omega ^2}LC{\rm{ }} = {\rm{ }}1\)

Ta có, độ lệch pha của u so với i: \(\Delta \varphi  = \frac{\pi }{6} - \frac{\pi }{3} =  - \frac{\pi }{6}\)

Công suất tiêu thụ của đoạn mạch: \(P = UI\cos \varphi  = \frac{{100}}{{\sqrt 2 }}.\frac{2}{{\sqrt 2 }}.\cos \left( { - \frac{\pi }{6}} \right) = 50\sqrt 3 {\rm{W}}\)

Ta có: \({\rm{cos}}\varphi  = \dfrac{R}{Z}\)

Mạch chỉ có C có hệ số công suất nhỏ nhất vì \(cos\varphi  = 0\)

+ Ta có, hệ số công suất: \(cos\varphi  = \dfrac{R}{Z} = k\)

+ Mạch có tính cảm kháng: \({Z_L} > {Z_C}\)

+ Độ lớn hiệu số cảm kháng và dung kháng: \(\left| {{Z_L} - {Z_C}} \right| = \left| {\omega L - \dfrac{1}{{\omega C}}} \right| = \left| {2\pi fL - \dfrac{1}{{2\pi fC}}} \right|\)

Khi ta giảm tần số của dòng điện thì khi đó:

+ Hiệu số cảm kháng và dung kháng giảm dần về 0, khi đó hệ số công suất tăng dần đến \({k_0}\)

+ Sau đó độ lớn hiệu số cảm kháng và dung kháng tăng dần từ 0 đến giá trị nào đó => hệ số công suất \(k\) giảm từ \({k_0}\)

Vậy khi giảm tần số của dòng điện thì hệ số công suất k tăng lên rồi giảm

Ta có: Công suất \(P = UIcos\varphi  = {\rm{ }}UI\dfrac{R}{Z} = \dfrac{U}{Z}IR = {I^2}R\)

=> Công suất không phụ thuộc vào pha ban đầu của dòng điện qua mạch

Ta có, biểu thức tính độ lệch pha của u so với i: \(\tan \varphi  = \dfrac{{{Z_L} - {Z_C}}}{R}\)

Theo đề bài, ta có dòng điện sớm pha hơn hiệu điện thế một góc nhỏ hơn \(\dfrac{\pi }{2}\)

=> Mạch gồm R, L,C với \({Z_L} < {Z_C}\)  hoặc mạch chỉ gồm tụ điện và điện trở R

Ta xét các phương án:

+ A – sai vì: mạch có thể có cuộn cảm với \({Z_L} < {Z_C}\)

+ B – sai vì: hệ số công suất của mạch khác không ( do mạch gồm R, L,C với \({Z_L} < {Z_C}\)  hoặc mạch chỉ gồm tụ điện và điện trở R mà hệ số công suất \(cos\varphi  = \dfrac{R}{Z}\) => \(cos\varphi  \ne 0\))

+ C – đúng vì: Ta có, cường độ dòng điện hiệu dụng qua đoạn mạch: \(I = \dfrac{U}{Z} = \dfrac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)

=> Khi ta tăng tần số dòng điện lên thì cảm kháng tăng và dung kháng giảm => tổng trở của mạch tăng => cường độ dòng điện trong mạch giảm

+ D – sai vì: Ta có, cường độ dòng điện hiệu dụng qua đoạn mạch: \(I = \dfrac{U}{Z} = \dfrac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)

=> Khi ta tăng tần số dòng điện lên thì cảm kháng tăng và dung kháng giảm => tổng trở của mạch tăng => cường độ dòng điện trong mạch giảm

Ta có, mạch RLC mắc nối tiếp có hệ số công suất lớn nhất khi: \({Z_L} = {Z_C}\)

Khi đó, ta có:

+ \(\omega  = \dfrac{1}{{\sqrt {LC} }} \to T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {LC} \)

+ Công suất cực đại: \({P_{{\rm{max}}}} = UI\)

+ Tổng trở khi đó: \(Z = R\)

+ \(U = {U_R}\)

=> Các phương án:

A – đúng

B, C, D - sai

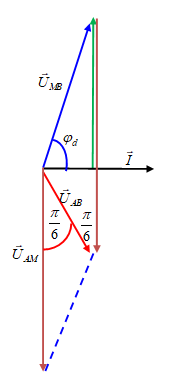
 + Dễ dàng nhận ra cuộn dây có điện trở thuần => \(0 < \varphi  < {90^0}\).

+ Áp dụng hàm sin trong tam giác, ta có: \(\dfrac{{{U_{MB}}}}{{\sin \dfrac{\pi }{6}}} = \dfrac{{{U_{AM}}}}{{\sin ({\varphi _d} + \dfrac{\pi }{3})}}\).

+ Chuẩn hóa: U_MB =1 => \({U_{AM}} = \sqrt 2 .\)  \(\sin ({\varphi _d} + \dfrac{\pi }{3}) = \dfrac{1}{{\sqrt 2 }} \to \left\{ \begin{array}{l}{\varphi _d} + \dfrac{\pi }{3} = \dfrac{\pi }{4} \to {\varphi _d} < 0:loai\\{\varphi _d} + \dfrac{\pi }{3} = \dfrac{{3\pi }}{4} \to {\varphi _d} = \dfrac{{5\pi }}{{12}}\end{array} \right.\)

+ Hệ số công suất của cuộn dây: \({\rm{cos}}{\varphi _d} = c{\rm{os}}\dfrac{{5\pi }}{{12}} = \)\(\dfrac{{\sqrt 6  - \sqrt 2 }}{4}\)

Ta có:

+ Độ lệch pha của u so với i: \(\varphi  = \dfrac{{2\pi }}{3} - \dfrac{\pi }{4} = \dfrac{{5\pi }}{{12}}\)

+ Hiệu điện thế hiệu dụng: \(U = 80V\)

Cường độ dòng điện hiệu dụng: \(I = \dfrac{4}{{\sqrt 2 }} = 2\sqrt 2 A\)

=> Công suất tiêu thụ của mạch điện: \(P = UIcos\varphi  = 80.2\sqrt 2 .cos\dfrac{{5\pi }}{{12}} = 58,56W\)

Ta có:

+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{{0,5}}{\pi } = 50\Omega \)

+ Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{5.10}^{ - 4}}}}{{3\pi }}}} = 60\Omega \)

+ Tổng trở của mạch: \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}}  = \sqrt {{{24}^2} + {{(50 - 60)}^2}}  = 26\Omega \)

+ Cường độ dòng điện hiệu dụng trong mạch: \(I = \dfrac{U}{Z} = \dfrac{{65}}{{26}} = 2,5(A)\)

+ Công suất tỏa nhiệt : \(P = {I^2}R = 2,{5^2}.24 = 150{\rm{W}}\)

Công suất tiêu thụ của đoạn mạch là \(P = R{I^2} = 100.{\left( {\sqrt 2 } \right)^2} = 200W\)

Ta có:

Công suất tiêu thụ của mạch điện: \(P = UIcos\varphi  \to I = \dfrac{P}{{Uc{\rm{os}}\varphi }} = \dfrac{{100}}{{220.0,6}} = 0,7575(A)\)

Tổng trở : \(Z = \dfrac{U}{I} = \dfrac{{220}}{{0,7575}} = 290,4\Omega \)

Hệ số công suất : \({\rm{cos}}\varphi  = \dfrac{R}{Z} = 0,6 \to R = 0,6.Z = 0,6.290,4 = 174,24\Omega \)

Ta có:

+ Công suất tiêu thụ của mạch điện: \(P = \dfrac{{{U^2}}}{{{Z^2}}}R\)

+ Do mạch là cuộn dây có điện trở thuần và độ tự cảm L => tổng trở của mạch: \(Z = \sqrt {{R^2} + {Z_L}^2} \)

\( \to P = \dfrac{{{U^2}}}{{{R^2} + Z_L^2}}R \leftrightarrow 100 = \dfrac{{{{110}^2}}}{{{{50}^2} + {Z_L}^2}}50 \to {Z_L} = 59,6\Omega \)

+ Mặt khác, ta có: \({Z_L} = \omega L = 2\pi fL \to L = \dfrac{{{Z_L}}}{{2\pi f}} = \dfrac{{59,6}}{{2\pi .60}} = 0,158(H)\)

Ta có:

+ Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 3}}}}{{3\pi }}}} = 30\Omega \)

+ Tổng trở của mạch: \(Z = \sqrt {{R^2} + {Z_C}^2}  = \sqrt {{{40}^2} + {{30}^2}}  = 50\Omega \)

+ hệ số công suất: \({\rm{cos}}\varphi  = \dfrac{R}{Z} = \dfrac{{40}}{{50}} = 0,8\)

Ta có:

+  Điện áp hiệu dụng hai đầu đoạn mạch:

\(\begin{array}{l}U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}}  \leftrightarrow {U^2} = U_R^2 + {\left( {\dfrac{U}{{\sqrt 2 }} - \sqrt 2 U} \right)^2}\\ \leftrightarrow {U^2} = U_R^2 + \dfrac{{{U^2}}}{2}\\ \leftrightarrow U_R^2 = \dfrac{{{U^2}}}{2} \to {U_R} = \dfrac{U}{{\sqrt 2 }}\end{array}\)

+ Hệ số công suất: \({\rm{cos}}\varphi  = \dfrac{R}{Z} = \dfrac{{{U_R}}}{U} = \dfrac{{\dfrac{U}{{\sqrt 2 }}}}{U} = \dfrac{1}{{\sqrt 2 }}\)

+ Xét đoạn mạch AM: \(\left\{ \begin{array}{l}{R_1} = {Z_C} = 40\Omega  \Rightarrow {\varphi _{AM}} =  - \dfrac{\pi }{4}\\{Z_{AM}} = 40\sqrt 2  \Rightarrow I = \dfrac{{{U_{AM}}}}{{{Z_{AM}}}} = 0,625\sqrt 2 A\end{array} \right.\)

Theo đề bài, \({u_{MB}}\) nhanh pha hơn \({u_{AM}}\) góc \(\dfrac{\pi }{4}\) nên nhanh pha hơn i góc \(\dfrac{\pi }{3}\)

\(\begin{array}{l} \to \tan \varphi  = \dfrac{{{Z_L}}}{{{R_2}}} = \sqrt 3 \\ \to {Z_L} = \sqrt 3 {R_2}\end{array}\)

+ Xét đoạn mạch MB:

\(\begin{array}{l}{Z_{MB}} = \dfrac{{{U_{MB}}}}{I} = 120 = \sqrt {R_2^2 + Z_L^2}  = 2{R_2}\\ \to \left\{ \begin{array}{l}{R_2} = 60\Omega \\{Z_L} = 60\sqrt 3 \Omega \end{array} \right.\end{array}\)

Hệ số công suất của mạch AB là  \(cos\varphi  = \dfrac{{{R_1} + {R_2}}}{{\sqrt {{{({R_1} + {R_2})}^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{{40 + 60}}{{\sqrt {{{\left( {40 + 60} \right)}^2} + \left( {60\sqrt 3  - 40} \right)} }} \approx 0,84\)

Hiệu điện thế của đoạn mạch là tổng hợp của 2 thành phần:

+ Phần không đổi: U’=100V phần này không tạo ra dòng điện vì đoạn mạch chứa C ( Tụ điện không cho dòng điện không đổi đi qua)

+ Phần xoay chiều: \(u = 220\sqrt 2 {\rm{cos(100}}\pi {\rm{t + }}\dfrac{\pi }{4})V\)

Tổng trở của đoạn mạch là:

\(\begin{array}{l}Z = \sqrt {{R^2} + Z_C^2}  = \sqrt {{{50}^2} + {{50}^2}}  = 50\sqrt 2 \\ \to I = \dfrac{U}{Z} = \dfrac{{220}}{{50\sqrt 2 }} = 2,2\sqrt 2 A\end{array}\)

Công suất tiêu thụ của mạch là: \(P = {I^2}R = {\left( {2,2\sqrt 2 } \right)^2}.50 = 484{\rm{W}}\)

Ta có:

\(\begin{array}{l}L = {R^2}C = {r^2}C \leftrightarrow \dfrac{L}{C} = {R^2} = {r^2}\\ \to {Z_L}.{Z_C} = {R^2} = {r^2}\end{array}\)

Điện áp hiệu dụng của đoạn mạch RC gấp \(\sqrt 3 \) lần điện áp hiệu dụng hai đầu cuộn dây

\(\begin{array}{l}I.\sqrt {{R^2} + Z_C^2}  = \sqrt 3 .I.\sqrt {{r^2} + Z_L^2} \\ \leftrightarrow {R^2} + Z_C^2 = 3({r^2} + Z_L^2)\\ \leftrightarrow {Z_L}.{Z_C} + Z_C^2 = 3{Z_L}.{Z_C} + 2Z_L^2\\ \leftrightarrow {Z_C}({Z_L} + {Z_C}) = 3{Z_L}({Z_L} + {Z_C})\\ \to {Z_C} = 3{Z_L}\\ \to {R^2} = 3Z_L^2\\ \to R = \sqrt 3 Z{}_L\end{array}\)

=> Hệ số công suất của đoạn mạch là:

\(\cos \varphi  = \dfrac{{R + r}}{{\sqrt {{{(R + r)}^2} + {{({Z_L} - Zc)}^2}} }} = \dfrac{{2R}}{{\sqrt {4{R^2} + 4Z_L^2} }} = \dfrac{{2\sqrt 3 {Z_L}}}{{\sqrt {4.3.Z_L^2 + 4Z_L^2} }} = \dfrac{\sqrt 3}{2}\)

Hệ số công suất: \(\cos \varphi  = \dfrac{R}{Z} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {L\omega  - \dfrac{1}{{C\omega }}} \right)}^2}} }}\)

Từ phương trình điện áp và cường độ dòng điện, ta có:

+ Độ lệch pha của \(u\) so với \(i\): \(\varphi ={ - \dfrac{\pi }{4} - \dfrac{\pi }{{12}}}=-\dfrac{\pi}{3}\)

+ Điện áp hiệu dụng: \(U=\dfrac{U_0}{\sqrt{2}}=\dfrac{100}{\sqrt{2}}=50\sqrt{2}V\)

+ Cường độ dòng điện hiệu dụng: \(I=\dfrac{I_0}{\sqrt{2}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}A\)

=> Công suất tiêu thụ của đoạn mạch là : \(P = UI\cos \varphi  = 50\sqrt 2 .\sqrt 2 .\cos \left( -\dfrac{\pi}{3} \right) = 50W\)