Câu hỏi:
2 năm trước
Cho mạch điện xoay chiều AB gồm hai đoạn mạch AM chỉ chứa C và đoạn mạch MB chỉ chứa cuộn dây mắc nối tiếp. Biết UAM =\(\sqrt 2 \)UMB và uAB nhanh pha \(\dfrac{\pi }{6}\)so với uAM. Biết hệ số công suất của cuộn dây không vượt quá giá trị \(0,72\). Hệ số công suất của cuộn dây bằng
Trả lời bởi giáo viên
Đáp án đúng: b
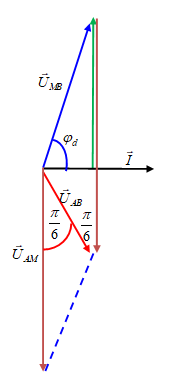
+ Dễ dàng nhận ra cuộn dây có điện trở thuần => \(0 < \varphi < {90^0}\).
+ Áp dụng hàm sin trong tam giác, ta có: \(\dfrac{{{U_{MB}}}}{{\sin \dfrac{\pi }{6}}} = \dfrac{{{U_{AM}}}}{{\sin ({\varphi _d} + \dfrac{\pi }{3})}}\).
+ Chuẩn hóa: UMB =1 => \({U_{AM}} = \sqrt 2 .\) \(\sin ({\varphi _d} + \dfrac{\pi }{3}) = \dfrac{1}{{\sqrt 2 }} \to \left\{ \begin{array}{l}{\varphi _d} + \dfrac{\pi }{3} = \dfrac{\pi }{4} \to {\varphi _d} < 0:loai\\{\varphi _d} + \dfrac{\pi }{3} = \dfrac{{3\pi }}{4} \to {\varphi _d} = \dfrac{{5\pi }}{{12}}\end{array} \right.\)
+ Hệ số công suất của cuộn dây: \({\rm{cos}}{\varphi _d} = c{\rm{os}}\dfrac{{5\pi }}{{12}} = \)\(\dfrac{{\sqrt 6 - \sqrt 2 }}{4}\)
Hướng dẫn giải:
Sử dụng giản đồ vec tơ
Áp dụng định lý hàm số sin: \(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}\)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
