Bài tập mạch xoay chiều RLC - có ω (hay f, T) thay đổi

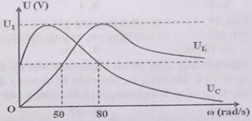
- Từ đồ thị ta thấy :

+ Có 2 giá trị của ω để U_C  bằng nhau là: \(\left[ \matrix{
{\omega _1} = 0 \hfill \cr
{\omega _2} = 80rad/s \hfill \cr} \right.\)

→ Giá trị ω_C để U_Cmax là : \(\omega _C^2 = \displaystyle{1 \over 2}\left( {\omega _1^2 + \omega _2^2} \right) = \displaystyle{1 \over 2}\left( {{0^2} + {{80}^2}} \right) \Rightarrow {\omega _C} = 40\sqrt 2 \left( {rad/s} \right)\)

+ Có 2 giá trị của ω để U_L  bằng nhau là: \(\left[ \matrix{
{\omega _1} = 50rad/s \hfill \cr
{\omega _2} = \infty \hfill \cr} \right.\)

→ Giá trị ω_L để U_Lmax là : \(\displaystyle{2 \over {\omega _L^2}} = {1 \over {\omega _1^2}} + {1 \over {\omega _2^2}} = {1 \over {{{50}^2}}} + {1 \over {{\infty ^2}}} \Rightarrow {\omega _L} = 50\sqrt 2 \left( {rad/s} \right)\)

- Mặt khác áp dụng công thức :

 \({U_{L\max }} = {U_{C\max }} = \displaystyle{U \over {\sqrt {1 - {\displaystyle{\left( {{{{\omega _L}} \over {{\omega _C}}}} \right)}^2}} }} = {{60} \over {\sqrt {1 - {{\left( {\displaystyle{{50\sqrt 2 } \over {40\sqrt 2 }}} \right)}^{ - 2}}} }} = 100V\)

Công suất trong mạch có giá trị cực đại là:

\({P_{\max }} = \dfrac{{{U^2}}}{R} = \dfrac{{{{\left( {110\sqrt 2 } \right)}^2}}}{{110}} = 220\,\,\left( {\rm{W}} \right)\)

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}\dfrac{1}{{{\omega _0}C}} = 90\Omega \\{\omega _0}L = 10\Omega \end{array} \right.\\ \to \dfrac{{{Z_L}}}{{{Z_C}}} = \omega _0^2LC = \dfrac{{10}}{{90}} = \dfrac{1}{9}\\ \to \omega _0^2 = \dfrac{1}{{9LC}}\end{array}\)

Khi mạch cộng hưởng: \({\omega ^2} = \dfrac{1}{{LC}} = 9\omega _0^2 \to \omega  = 3{\omega _0}\)

Ta có:

+ Điện áp: \(u = 120cos\left( {\omega t + \dfrac{\pi }{3}} \right)V\)

+ Cường độ dòng điện: \(i = {I_0}cos\left( {\omega t + \dfrac{\pi }{3}} \right)A\)

Nhận thấy pha của điện áp và cường độ dòng điện như nhau hay nói cách khác u, i cùng pha với nhau

=> mạch cộng hưởng

Khi đó \({u_R} = u\)

Điện áp hiệu dụng trên điện trở bằng điện áp hiệu dụng của mạch: \({U_R} = U = \dfrac{{120}}{{\sqrt 2 }} = 60\sqrt 2 V\)

Gọi \(\omega_1;\omega_2\) lần lượt là tần số góc trong 2 trường hợp trên

Ta có:

\(\begin{array}{l}\omega _1^2 = \dfrac{1}{{{L_1}{C_1}}};\omega _2^2 = \dfrac{1}{{{L_2}{C_2}}}\\{\omega _1} = {\omega _2} \to {L_1}{C_1} = {L_2}{C_2} \to \dfrac{{{L_2}}}{{{L_1}}} = \dfrac{{{C_1}}}{{{C_2}}}\\ \to {\omega ^2} = \dfrac{1}{{({L_1} + {L_2})\dfrac{{{C_1}C{}_2}}{{{C_1} + {C_2}}}}} = \dfrac{1}{{\left( {1 + \dfrac{{{L_2}}}{{{L_1}}}} \right)\dfrac{{{L_1}{C_1}}}{{\dfrac{{{C_1}}}{{{C_2}}} + 1}}}} = \dfrac{1}{{{L_1}{C_1}}} = \omega _1^2\\ \to \omega  = {\omega _1}\\ \to f = {f_1}\end{array}\)

Ta có: \(f\) thay đổi để công suất trong mạch đạt giá trị cực đại khi đó: \({Z_L} = {Z_C}\) và \({P_{ma{\rm{x}}}} = \dfrac{{{U^2}}}{R}\)

\( \to {P_{ma{\rm{x}}}} = \dfrac{{{{\left( {\dfrac{{120}}{{\sqrt 2 }}} \right)}^2}}}{{40}} = 180{\rm{W}}\)

\({f_1} = 50Hz \to {\omega _1} = 100\pi \left( {rad/s} \right)\)

Theo đầu bài, ta có:

\(\begin{array}{l}{Z_{{C_1}}} = 6,25{Z_{{L_1}}} \leftrightarrow \dfrac{1}{{{\omega _1}C}} = 6,25{\omega _1}L\\ \to {\omega _1}^2 = \dfrac{1}{{6,25LC}}{\rm{         (1)}}\end{array}\)

+ Để công suất trong mạch đạt giá trị cực đại <=>\({Z_L} = {Z_C}\) hay \({\omega _0} = \dfrac{1}{{\sqrt {LC} }}\) (2)

Từ (1) và (2), ta suy ra:

\(\begin{array}{l}{\omega _0} = \sqrt {6,25} {\omega _1}\\ \to {f_0} = \sqrt {6,25} {f_1} = 2,5.50 = 125(H{\rm{z}})\end{array}\)

Ta có:

+ Khi \(f = {f_1}\): \(\left\{ \begin{array}{l}{Z_{{L_1}}} = 48\Omega  = {\omega _1}L = 2\pi {f_1}.L\\{Z_{{C_1}}} = 60\Omega  = \dfrac{1}{{{\omega _1}C}} = \dfrac{1}{{2\pi {f_1}C}}\end{array} \right.\)

Ta suy ra:

\(\begin{array}{l}\dfrac{{{Z_{{L_1}}}}}{{{Z_{{C_1}}}}} = \dfrac{{48}}{{60}} = \dfrac{4}{5} = \omega _1^2LC\\ \to \omega _1^2 = \dfrac{4}{{5LC}}\end{array}\)

+ Khi \(f = {f_2}\), hệ số công suất \(cos\varphi  = 1 \to \) mạch cộng hưởng

\(\begin{array}{l} \to {Z_{{L_2}}} = {Z_{{C_2}}} \leftrightarrow {\omega _2}L = \dfrac{1}{{{\omega _2}C}}\\ \to \omega _2^2 = \dfrac{1}{{LC}}\end{array}\)

Từ đó, ta suy ra: \(\dfrac{{\omega _1^2}}{{\omega _2^2}} = \dfrac{4}{5} \to {\omega _2} = \dfrac{{\sqrt 5 }}{2}{\omega _1} \to {f_2} = \dfrac{{\sqrt 5 }}{2}{f_1}\)

Theo đầu bài, ta có:

\(\begin{array}{l}{Z_1} = {Z_2} \leftrightarrow Z_1^2 = Z_2^2\\ \leftrightarrow {R^2} + {\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)^2} = {R^2} + {\left( {{Z_{{L_2}}} - {Z_{{C_2}}}} \right)^2}\\ \to \left| {{Z_{{L_1}}} - {Z_{{C_1}}}} \right| = \left| {{Z_{{L_2}}} - {Z_{{C_2}}}} \right|\\ \to \left[ \begin{array}{l}{Z_{{L_1}}} + {Z_{{L_2}}} = {Z_{{C_1}}} + {Z_{{C_2}}}\\{Z_{{L_1}}} - {Z_{{C_1}}} = {Z_{{L_2}}} - {Z_{{C_2}}}(L)\end{array} \right.\end{array}\)

Ta suy ra:

\(\begin{array}{l}{Z_{{L_1}}} + {Z_{{L_2}}} = {Z_{{C_1}}} + {Z_{{C_2}}}\\ \leftrightarrow {\omega _1}L + {\omega _2}L = \dfrac{1}{{{\omega _1}C}} + \dfrac{1}{{{\omega _2}C}}\\ \leftrightarrow \left( {{\omega _1} + {\omega _2}} \right)L = \left( {\dfrac{1}{{{\omega _1}}} + \dfrac{1}{{{\omega _2}}}} \right)\dfrac{1}{C}\\ \leftrightarrow \left( {{\omega _1} + {\omega _2}} \right)L = \left( {\dfrac{{{\omega _1} + {\omega _2}}}{{{\omega _1}{\omega _2}}}} \right)\dfrac{1}{C}\\ \to {\omega _1}{\omega _2} = \dfrac{1}{{LC}}\end{array}\)

Ta có, hệ số công suất \(cos\varphi  = \dfrac{R}{Z}\)

Theo đề bài

\(\begin{array}{l}cos{\varphi _1} = cos{\varphi _2} \leftrightarrow \dfrac{R}{{{Z_1}}} = \dfrac{R}{{{Z_2}}}\\ \to {Z_1} = {Z_2}\end{array}\)

\(\begin{array}{l}{Z_1} = {Z_2} \leftrightarrow Z_1^2 = Z_2^2\\ \leftrightarrow {R^2} + {\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)^2} = {R^2} + {\left( {{Z_{{L_2}}} - {Z_{{C_2}}}} \right)^2}\\ \to \left| {{Z_{{L_1}}} - {Z_{{C_1}}}} \right| = \left| {{Z_{{L_2}}} - {Z_{{C_2}}}} \right|\\ \to \left[ \begin{array}{l}{Z_{{L_1}}} + {Z_{{L_2}}} = {Z_{{C_1}}} + {Z_{{C_2}}}\\{Z_{{L_1}}} - {Z_{{C_1}}} = {Z_{{L_2}}} - {Z_{{C_2}}}(L)\end{array} \right.\end{array}\)

\(\begin{array}{l}{Z_{{L_1}}} + {Z_{{L_2}}} = {Z_{{C_1}}} + {Z_{{C_2}}}\\ \leftrightarrow {\omega _1}L + {\omega _2}L = \dfrac{1}{{{\omega _1}C}} + \dfrac{1}{{{\omega _2}C}}\\ \leftrightarrow \left( {{\omega _1} + {\omega _2}} \right)L = \left( {\dfrac{1}{{{\omega _1}}} + \dfrac{1}{{{\omega _2}}}} \right)\dfrac{1}{C}\\ \leftrightarrow \left( {{\omega _1} + {\omega _2}} \right)L = \left( {\dfrac{{{\omega _1} + {\omega _2}}}{{{\omega _1}{\omega _2}}}} \right)\dfrac{1}{C}\\ \to {\omega _1}{\omega _2} = \dfrac{1}{{LC}}\\ \to {\omega _2}L = \dfrac{1}{{{\omega _1}C}}\\ \to {Z_{{L_2}}} = {Z_{{C_1}}}\end{array}\)

Thay vào biểu thức tính hệ số công suất, ta được:

\(\begin{array}{l}cos{\varphi _1} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)}^2}} }} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_{{L_1}}} - {Z_{{L_2}}}} \right)}^2}} }}\\ = \dfrac{R}{{\sqrt {{R^2} + {L^2}{{\left( {{\omega _1} - {\omega _2}} \right)}^2}} }}\end{array}\)

Lại có \(L = C{R^2} \to {R^2} = \dfrac{L}{C}\) , thay vào biểu thức trên, ta được:

\(\begin{array}{l}cos{\varphi _1} = \dfrac{{\sqrt {\dfrac{L}{C}} }}{{\sqrt {\dfrac{L}{C} + {L^2}{{\left( {{\omega _1} - {\omega _2}} \right)}^2}} }} = \sqrt {\dfrac{1}{{1 + LC{{\left( {{\omega _1} - {\omega _2}} \right)}^2}}}} \\ = \dfrac{1}{{\sqrt {1 + \dfrac{1}{{{\omega _1}{\omega _2}}}{{\left( {{\omega _1} - {\omega _2}} \right)}^2}} }} = \dfrac{1}{{\sqrt {1 + \dfrac{{{{\left( {60\pi  - 180\pi } \right)}^2}}}{{60\pi .180\pi }}} }} = \sqrt {\dfrac{3}{7}} \end{array}\)

Theo đầu bài, ta có: \(C{R^2} < 2L \leftrightarrow {R^2} < 2\dfrac{L}{C} \to {R^2} < 2{Z_L}{Z_C}\) hay \(\dfrac{{{Z_L}}}{R}\dfrac{{{Z_C}}}{R} > \dfrac{1}{2}\)

Khi \(\omega \) thay đổi, để  điện áp hai đầu tụ C cực đại thì ta có:

\(\left| {\tan \varphi .\tan {\varphi _{RL}}} \right| = \dfrac{1}{2}\)

Lại có: \(\tan {\varphi _{RL}} = \dfrac{{{Z_L}}}{R} = \dfrac{{{U_L}}}{{{U_R}}} = \dfrac{1}{5}\)

\(\begin{array}{l} \to \left| {\tan \varphi .\dfrac{{{Z_L}}}{R}} \right| = \dfrac{1}{2} \leftrightarrow \tan \varphi .\dfrac{1}{5} = \dfrac{1}{2}\\ \to \tan \varphi  = \dfrac{5}{2}\\ \leftrightarrow \dfrac{{\sin \varphi }}{{cos\varphi }} = \dfrac{5}{2} \leftrightarrow \dfrac{{\sqrt {1 - co{s^2}\varphi } }}{{cos\varphi }} = \dfrac{5}{2}\\ \to co{s^2}\varphi  = \dfrac{4}{{29}}\\ \to c{\rm{os}}\varphi  = \dfrac{2}{{\sqrt {29} }}\end{array}\)

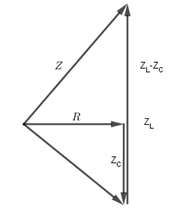
Ta có: \({U_{{L_{max}}}} = I.{Z_L} = \dfrac{U}{Z}.{Z_L}\)

Theo đầu bài, ta có: \({U_{Lmax}} = \dfrac{{26}}{{24}}U\)

Ta có thể giả sử: \(Z = 24\Omega ;{Z_L} = 26\Omega \)

Khi đó:

\(\begin{array}{l}Z_L^2 = {Z^2} + Z_C^2\\ \Rightarrow {Z_C} = \sqrt {Z_L^2 - {Z^2}}  = \sqrt {{{26}^2} - {{24}^2}}  = 10\Omega \end{array}\)

Lại có:

\(\begin{array}{l}\dfrac{{{R^2}}}{2} = {Z_C}\left( {{Z_L} - {Z_C}} \right)\\ \Rightarrow R = \sqrt {2{Z_C}\left( {{Z_L} - {Z_C}} \right)}  = \sqrt {2.10\left( {26 - 10} \right)}  = 8\sqrt 5 \Omega \end{array}\)

Hệ số công suất của mạch khi đó: \(cos\varphi  = \dfrac{R}{Z} = \dfrac{{8\sqrt 5 }}{{24}} = \dfrac{{\sqrt 5 }}{3}\)

Ta có:

\(\tan \alpha  = \tan \left( {{\varphi _{RC}} - {\varphi _{RLC}}} \right) = \dfrac{{\tan {\varphi _{RC}} - \tan {\varphi _{RLC}}}}{{1 + \tan {\varphi _{RC}}\tan {\varphi _{RLC}}}}\)

Đặt: \(\left\{ \begin{array}{l}\tan {\varphi _{RC}} = x\\\tan {\varphi _{RLC}} = y\end{array} \right.\)

\( \Rightarrow \tan \alpha  = \dfrac{{x - y}}{{1 + xy}}\) (1)

Mặt khác, ta có khi \(\omega \) thay đổi để \({U_{{L_{max}}}}\) thì \(\tan {\varphi _{RC}}\tan \varphi  =  - \dfrac{1}{2}\) hay \(xy =  - \dfrac{1}{2}\)

Thay vào (1) ta được: \(\tan \alpha  = \dfrac{{x + \dfrac{1}{{2x}}}}{{1 + \left( { - \dfrac{1}{2}} \right)}} = 2x + \dfrac{1}{x}\)

Lại có \(2x + \dfrac{1}{x} \ge 2\sqrt {2x.\dfrac{1}{x}}  = 2\sqrt 2 \)

\(\begin{array}{l} \Rightarrow \tan \alpha  \ge 2\sqrt 2 \\ \Rightarrow \alpha  \ge 70,{53^0}\end{array}\)

Ta có:

\(\begin{array}{l}{P_1} = {P_2} \Leftrightarrow I_1^2R = I_2^2R \Leftrightarrow I_1^2 = I_2^2\\ \to \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}} = \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L2}} - {Z_{C2}})}^2}}}\\ \to {({Z_{L1}} - {Z_{C1}})^2} = {({Z_{L2}} - {Z_{C2}})^2} \to \left( \begin{array}{l}{Z_{L1}} - {Z_{C1}} = {Z_{L2}} - {Z_{C2}}(loai)\\{Z_{L1}} - {Z_{C1}} =  - ({Z_{L2}} - {Z_{C2}})\end{array} \right.\\ \to {Z_{L1}} + {Z_{L2}} = {Z_{C1}} + {Z_{C2}}) \to L({\omega _1} + {\omega _2}) = \dfrac{1}{C}(\dfrac{1}{{{\omega _1}}} + \dfrac{1}{{{\omega _2}}}) = \dfrac{1}{C}\dfrac{{{\omega _1} + {\omega _2}}}{{{\omega _1}{\omega _2}}}\\ \to {\omega _1}{\omega _2} = \dfrac{1}{{LC}} = \omega _0^2\end{array}\)

\(\begin{array}{l}I_1^2 = I_2^2\\ \to \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}} = \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L2}} - {Z_{C2}})}^2}}}\\ \to {({Z_{L1}} - {Z_{C1}})^2} = {({Z_{L2}} - {Z_{C2}})^2} \to \left[ \begin{array}{l}{Z_{L1}} - {Z_{C1}} = {Z_{L2}} - {Z_{C2}}(loai)\\{Z_{L1}} - {Z_{C1}} =  - ({Z_{L2}} - {Z_{C2}})\end{array} \right.\\ \to {Z_{L1}} + {Z_{L2}} = {Z_{C1}} + {Z_{C2}}) \to L({\omega _1} + {\omega _2}) = \dfrac{1}{C}(\dfrac{1}{{{\omega _1}}} + \dfrac{1}{{{\omega _2}}}) = \dfrac{1}{C}\dfrac{{{\omega _1} + {\omega _2}}}{{{\omega _1}{\omega _2}}}\\ \to {\omega _1}{\omega _2} = \dfrac{1}{{LC}} = \omega _0^2\end{array}\)

Với \({\omega _0}\): tần số góc của vật khi mạch cộng hưởng (hay có cường độ dòng điện cực đại)

\( \Rightarrow {\omega _0} = \sqrt {{\omega _1}{\omega _2}}  = \sqrt {250\pi .90\pi }  = 150\pi \left( {rad/s} \right)\)

Ta có:

\(Z = {Z_C} = {Z_{L{\rm{r}}}} = 80\Omega \)

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}{Z^2} = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2}\\{r^2} + Z_L^2 = Z_{Lr}^2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{80^2} = {r^2} + {\left( {{Z_L} - 80} \right)^2}\\{r^2} + Z_L^2 = {80^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{Z_L} = 40\Omega \\r = 40\sqrt 3 \Omega \end{array} \right.\end{array}\)

\( \to {Z_C} = 2{Z_L} \to \dfrac{1}{{\omega C}} = 2\omega L \to \dfrac{1}{{LC}} = 2{\omega ^2}\)  (1)

Ta có, khi tăng điện dung thêm một lượng  \(\Delta C = \dfrac{1}{{8\pi }}\left( {mF} \right)\)

\(\omega _0^2 = \dfrac{1}{{L(C + \Delta C)}}\)  (2)

Từ (1) và (2) \( \to \dfrac{{{\omega ^2}}}{{\omega _0^2}} = \dfrac{{C + \Delta C}}{{2C}} \to \dfrac{{2{\omega ^2}}}{{\omega _0^2}} = 1 + \omega {Z_C}\Delta C\)

Thay số liệu vào rút ra được phương trình sau: 

\(\begin{array}{l}2{\omega ^2} = \omega _0^2 + \omega _0^2.{Z_C}\Delta C.\omega \\ \Leftrightarrow 2{\omega ^2} - {\left( {100\pi } \right)^2}.80.\left( {\dfrac{1}{{8\pi }}{{.10}^{ - 3}}} \right)\omega  - {\left( {100\pi } \right)^2} = 0\\ \Leftrightarrow 2{\omega ^2} - 100\pi \omega  - {\left( {100\pi } \right)^2} = 0\\ \Leftrightarrow {\omega ^2} - 50\pi \omega  - 5000{\pi ^2} = 0\\ \Rightarrow \left[ \begin{array}{l}\omega  = 100\pi \left( {rad/s} \right)\\\omega  =  - 50\pi \left( {rad/s} \right)\left( {loại} \right)\end{array} \right.\end{array}\)

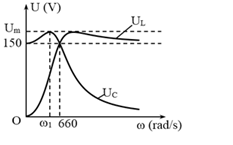
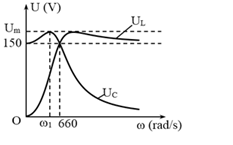
\(\omega  = {\omega _1}\) - thì hiệu điện thế hiệu dụng trên hai đầu tụ điện cực đại  \({U_{{C_{max}}}}\)

+ Từ đồ thị, ta có:

\(\omega  = \omega ' = 0\) và \(\omega  = {\omega _0} = 660\left( {rad/s} \right)\) đều cho \({U_C}\) như nhau

(Áp dụng bài toán \(\omega \) biến thiên có hai giá trị của \(\omega \) cho cùng hiệu điện thế \({U_C}\))

Khi đó ta có:

\(\omega _1^2 + \omega _2^2 = 2\omega _C^2 \Leftrightarrow \omega {'^2} + \omega _0^2 = 2\omega _1^2\)

\( \Rightarrow {\omega _1} = \dfrac{{{\omega _0}}}{{\sqrt 2 }}\)  (1)

+ Tại vị trí \(\omega  = 0\), \({U_C} = U = 150V\)

+ Tại vị trí: \(\omega  = {\omega _0} = 660\left( {rad/s} \right)\), ta có \({U_C} = {U_L} = {U_R} = U\)

Nên ta suy ra: \({Z_{0C}} = {Z_{0L}} = R\)  (2)

+ Tại vị trí: \(\omega  = {\omega _1}\)

\(\begin{array}{l}{U_C} = {U_{{C_{max}}}} = \dfrac{{U{Z_C}}}{Z} = \dfrac{{U{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ = \dfrac{{U\sqrt 2 {Z_{0C}}}}{{\sqrt {{R^2} + {{\left( {\dfrac{1}{{\sqrt 2 }}{Z_{0L}} - \sqrt 2 {Z_{0C}}} \right)}^2}} }} = \dfrac{{U\sqrt 2 R}}{{\sqrt {{R^2} + {{\left( {\dfrac{1}{{\sqrt 2 }}R - \sqrt 2 R} \right)}^2}} }}\\ = \dfrac{{U\sqrt 2 }}{{\sqrt {1 + \dfrac{1}{2}} }} = \dfrac{{U2\sqrt 3 }}{3}\end{array}\)

Lại có \(U = 150V\)

\( \Rightarrow {U_m} = {U_{{C_{max}}}} = \dfrac{{150.2\sqrt 3 }}{3} = 100\sqrt 3 V\)

\(\left\{ \begin{array}{l}\dfrac{1}{{{\omega _0}C}} = 25\Omega \\{\omega _0}L = 100\Omega \end{array} \right. \to \dfrac{{{Z_L}}}{{{Z_C}}} = \omega _0^2LC = 4 \to \omega _0^2 = \dfrac{4}{{LC}}\)

Khi mạch cộng hưởng: \({\omega ^2} = \dfrac{1}{{LC}} = \dfrac{{\omega _0^2}}{4} \to \omega  = \dfrac{{{\omega _0}}}{2}\) 

$u, i$ cùng pha => suy ra mạch cộng hưởng.

Khi đó: \(u = {\rm{ }}{u_R}{\rm{ }} =  > {\rm{ }}{U_R} = {\rm{ }}U{\rm{ }} = {\rm{ }}220{\rm{ }}V\)

Ta có:

\(\begin{array}{l}\omega _1^2 = \dfrac{1}{{{L_1}{C_1}}};\omega _2^2 = \dfrac{1}{{{L_2}{C_2}}}\\{\omega _1} = {\omega _2} \to {L_1}{C_1} = {L_2}{C_2} \to \dfrac{{{L_2}}}{{{L_1}}} = \dfrac{{{C_1}}}{{{C_2}}}\\ \to {\omega ^2} = \dfrac{1}{{({L_1} + {L_2})\dfrac{{{C_1}C{}_2}}{{{C_1} + {C_2}}}}} = \dfrac{1}{{\left( {1 + \dfrac{{{L_2}}}{{{L_1}}}} \right)\dfrac{{{L_1}{C_1}}}{{\dfrac{{{C_1}}}{{{C_2}}} + 1}}}} = \dfrac{1}{{{L_1}{C_1}}} = \omega _1^2\\ \to \omega  = {\omega _1}\end{array}\)