Câu hỏi:
2 năm trước
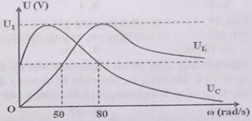
Đặt điện áp xoay chiều \(u = 60\sqrt 2 \cos \left( {\omega t} \right)\left( V \right)\), (ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở R, cuộn dây thuần cảm và tụ điện mắc nối tiếp. Hình bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng hai đầu tụ điện UC và điện áp hiệu dụng hai đầu cuộn dây UL theo tần số góc. Giá trị của U1 là :
Trả lời bởi giáo viên
Đáp án đúng: d
- Từ đồ thị ta thấy :
+ Có 2 giá trị của ω để UC bằng nhau là: \(\left[ \matrix{
{\omega _1} = 0 \hfill \cr
{\omega _2} = 80rad/s \hfill \cr} \right.\)
→ Giá trị ωC để UCmax là : \(\omega _C^2 = \displaystyle{1 \over 2}\left( {\omega _1^2 + \omega _2^2} \right) = \displaystyle{1 \over 2}\left( {{0^2} + {{80}^2}} \right) \Rightarrow {\omega _C} = 40\sqrt 2 \left( {rad/s} \right)\)
+ Có 2 giá trị của ω để UL bằng nhau là: \(\left[ \matrix{
{\omega _1} = 50rad/s \hfill \cr
{\omega _2} = \infty \hfill \cr} \right.\)
→ Giá trị ωL để ULmax là : \(\displaystyle{2 \over {\omega _L^2}} = {1 \over {\omega _1^2}} + {1 \over {\omega _2^2}} = {1 \over {{{50}^2}}} + {1 \over {{\infty ^2}}} \Rightarrow {\omega _L} = 50\sqrt 2 \left( {rad/s} \right)\)
- Mặt khác áp dụng công thức :
\({U_{L\max }} = {U_{C\max }} = \displaystyle{U \over {\sqrt {1 - {\displaystyle{\left( {{{{\omega _L}} \over {{\omega _C}}}} \right)}^2}} }} = {{60} \over {\sqrt {1 - {{\left( {\displaystyle{{50\sqrt 2 } \over {40\sqrt 2 }}} \right)}^{ - 2}}} }} = 100V\)
Hướng dẫn giải:
Sử dụng lí thuyết về mạch điện xoay chiều có ω thay đổi
+ Có 2 giá trị của ω để UC bằng nhau là ω1 và ω2 → Giá trị ωC để UCmax là :
\(\omega _C^2 = {1 \over 2}\left( {\omega _1^2 + \omega _2^2} \right)\)
+ Có 2 giá trị của ω để UL bằng nhau là ω1 và ω2 → Giá trị ωL để ULmax là :
\(\displaystyle{2 \over {\omega _L^2}} = {1 \over {\omega _1^2}} + {1 \over {\omega _2^2}}\)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
