Một ống Cu-lít-giơ (ống tia X) đang hoạt động. Bỏ qua động năng ban đầu của các êlectron khi bứt ra khỏi catôt. Ban đầu, hiệu điện thế giữa anôt và catôt là U thì tốc độ của êlectron khi đập vào anôt là v. Khi hiệu điện thế giữa anôt và catôt là 1,5U thì tốc độ của êlectron đập vào anôt thay đổi một lượng 4000 km/s so với ban đầu. Giá trị của v là
Ta có: \(\dfrac{1}{2}m{v^2} = eU\)
Suy ra: \(v = \sqrt {\dfrac{{2eU}}{m}} \) (1)
Lại có:
+ Khi \(U = U\) thì \(v = v\)
+ Khi \(U = 1,5U\) thì \(v = v'\)
Ta có: \(v' - v = 4000km/s = 4000.1000m/s\)
\(\begin{array}{l} \Leftrightarrow \sqrt {\dfrac{{2e.1,5U}}{m}} - \sqrt {\dfrac{{2e.U}}{m}} = 4000.1000\\ \Rightarrow \sqrt {\dfrac{{2eU}}{m}} \left( {\sqrt {1,5} - 1} \right) = 4000.1000\\ \Rightarrow \sqrt {\dfrac{{2eU}}{m}} = 1,{78.10^7}m/s\end{array}\)
Mặt khác, theo (1) ta có: \(v = \sqrt {\dfrac{{2eU}}{m}} = 1,{78.10^7}m/s\)
Cho chùm hẹp các electron quang điện có tốc độ 7,31.105 (m/s) và hướng nó vào một từ trường đều có cảm ứng từ 9,1.10-5 (T) theo hướng vuông góc với từ trường. Biết khối lượng và điện tích của electron lần lượt là 9,1.10-31 kg và -1,6.10-19 C. Xác định bán kính quỹ đạo các electron đi trong từ trường?
Khi e bay vào từ trường đều với quỹ đạo tròn thì lực Lorentz sẽ đóng vai trò là lực hướng tâm.
Ta có:
\({F_{ht}} = m{a_{ht}} \Leftrightarrow \left| e \right|vB = m\frac{{{v^2}}}{R} \to R = \frac{{mv}}{{\left| e \right|B}} = \frac{{9,{{1.10}^{ - 31}}.7,{{31.10}^5}}}{{1,{{6.10}^{ - 19}}.9,{{1.10}^{ - 5}}}} = 0,046m = 4,6cm\).
Chiếu bức xạ có bước sóng 533nm lên tấm kim loại có công thoát A = 3.10-19J. Dùng màn chắn tách ra một chùm hẹp các electron quang điện và cho bay vào từ trường theo phương vuông góc với đường cảm ứng từ. Biết bán kính cực đại của quỹ đạo của các electron quang điện là 22,75mm. Độ lớn cảm ứng từ B của từ trường là
Theo công thức Einstein về hiện tượng quang điện :
\(\frac{{hc}}{\lambda } = A + \frac{1}{2}{m_e}.v_{o\max }^2 \Rightarrow {v_{o\max }} = \sqrt {\frac{2}{{{m_e}}}\left( {\frac{{hc}}{\lambda } - A} \right)} = {4.10^5}(m/s)\) \(({m_e} = 9,{1.10^{ - 31}}kg)\)
Khi electron chuyển động trong từ trường đều có có hướng vuông góc với thì nó chịu tác dụng của lực Lorenxo f có độ lớn không đổi và luôn vuông góc với , nên electron chuyển động theo quỹ đạo là tròn và lực f đóng vai trò lực hướng tâm:
\({F_{ht}} = f \Leftrightarrow \frac{{{m_e}v_{o\max }^2}}{R} = \left| e \right|B{v_{o\max }} \Rightarrow B = \frac{{{m_e}.{v_{o\max }}}}{{\left| e \right|R}} = 1,{0.10^{ - 4}}(T)\)
Electron quang điện khi bật ra khỏi kim loại thì bay vào từ trường đều với cảm ứng từ B = 10-5 T theo quỹ đạo tròn mà hình chiếu của electron trên một đường kính sẽ dao động điều hòa với biên độ A = 10 cm. Cho khối lượng electron là 9,1.10-31 kg và điện tích electron là – 1,6.10-19C. Vận tốc electron có độ lớn là:
Khi e bay vào từ trường đều với quỹ đạo tròn thì lực Lorentz sẽ đóng vai trò là lực hướng tâm. Khi chiếu lên một đường kính, hình chiếu dao động điều hòa với A = 10 cm nên bán kính quỹ đạo tròn R = 10 cm.
Ta có
\({F_{ht}} = m{a_{ht}} \Leftrightarrow qvB = m\frac{{{v^2}}}{R} \Leftrightarrow v = \frac{{qBR}}{m} = 1,{76.10^5}(m/s)\).
Chiếu một bức xạ có bước sóng λ= 0, 48?m lên một tấm kim loại có công thoát A = 2,4.10-19J. dùng màn chắn tách ra một chùm hẹp các êlectron quang điện và hướng chúng bay theo chiều véc tơ cường độ điện trường có E = 1000 V/m. Quãng đường tối đa mà êlectron chuyển động được theo chiều véc tơ cường độ điện trường xấp xỉ là:
+ Theo công thức Anh - xtanh :
\(\dfrac{{hc}}{\lambda } = A + \dfrac{1}{2}m.{v_0}^2 \Rightarrow {v_0}^2 = \dfrac{2}{m}\left( {\dfrac{{hc}}{\lambda } - A} \right)\) \(({m_e} = 9,{1.10^{ - 31}}kg)\)
+ Ta có:
\(a = \dfrac{F}{m} = \dfrac{{qE}}{m}\)
+ Chuyển động của e là chuyển động chậm dần đều với vận tốc đầu v0 và gia tốc a
Electron dừng v = 0
\( \Leftrightarrow {0^2}-{\rm{ }}{v_0}^2 = {\rm{ }}2as \Rightarrow s = - \dfrac{{{v_0}^2}}{{2a}} = - \dfrac{{\dfrac{2}{m}\left( {\dfrac{{hc}}{\lambda } - A} \right)}}{{2.\dfrac{{qE}}{m}}} = - \dfrac{{\dfrac{{hc}}{\lambda } - A}}{{qE}} \Rightarrow s = 0,109cm\)
Cho chùm hẹp các electron quang điện và hướng nó vào một từ trường đều cảm ứng từ \(\;B = {10^{ - 4}}\left( T \right)\) theo phương vuông góc với từ trường. Biết khối lượng và điện tích của electron lần lượt là 9,1.10-31 kg và -1,6.10-19 C. Chu kì của electron trong từ trường là:
Khi e bay vào từ trường đều với quỹ đạo tròn thì lực Lorentz sẽ đóng vai trò là lực hướng tâm.
Ta có:
\({F_{ht}} = m{a_{ht}} \Leftrightarrow \left| e \right|vB = m\frac{{{v^2}}}{R} \to R = \frac{{mv}}{{\left| e \right|B}}\).
Mặt khác: tốc độ góc:
\(\omega = \frac{v}{R} = \frac{{\left| e \right|B}}{m}\)
Chu kì của electrong trong từ trường:
\(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\left| e \right|B}}.m = \frac{{2\pi }}{{1,{{6.10}^{ - 19}}{{.10}^{ - 4}}}}.9,{1.10^{ - 31}} = 3,{6.10^{ - 7}}(s) = 0,36\mu s\)
Chiếu ánh sáng có bước sóng \(5000\mathop A\limits^0 \) vào ca tốt của tế bào quang điện có công thoát e là 1,88eV. Sau đó tách ra một chùm hẹp các quang e có vận tốc \(\overrightarrow {{v_0}} \) rồi hướng vào miền không gian có điện trường đều có cường độ điện trường \(\overrightarrow E \) và từ trường đều cảm ứng từ \(\overrightarrow B \) sao cho \(\overrightarrow E ,\overrightarrow B ,\overrightarrow {{v_0}} \) vuông góc với nhau từng đôi một. Độ lớn cường độ điện trường là E = 2.104 V/m. Để e vẫn chuyển động thẳng đều không thay đổi hướng ban đầu của nó thì cảm ứng từ B có độ lớn là
Theo công thức Anh-xtanh ta tính được vận tốc của electron khi bay vào vùng có điện từ trường:
\(hf = A + \frac{1}{2}mv_0^2 = > {v_0} = 4,{61.10^6}(m/s)\)
Để electron bay vào điện từ trường mà vẫn chuyển động thẳng đều thì:
\({F_d} = f \Leftrightarrow e.E = e.{v_0}B \Rightarrow B = \frac{E}{{{v_0}}} = 4,{338.10^{ - 3}}(T)\)
Khi chiếu một photon có năng lượng 5,5eV vào tấm kim loại có công thoát 2eV. Cho rằng năng lượng mà quang electron hấp thụ một phần dùng để giải phóng nó, phần còn lại hoàn toàn biến thành động năng của nó. Tách ra một electron rồi cho bay từ M đến N trong một điện trường với hiệu điện thế UMN = -2V. Động năng của electron tại điểm N là:
Ta có:
\(\begin{array}{l}{{\rm{W}}_M} = {{\rm{W}}_A} + \left| e \right|{U_{MN}}\\ \to {{\rm{W}}_N} = \varepsilon - A + \left| e \right|{U_{MN}} = 5,5eV - 2eV - 2{\rm{e}}V = 1,5{\rm{e}}V\end{array}\)
Cho chùm hẹp các electron quang điện có tốc độ 106 (m/s) bay dọc theo đường sức trong một điện trường đều có cường độ 9,1 (V/m) sao cho hướng của vận tốc ngược hướng với điện trường. Tính quãng đường đi được sau thời gian 1000ns. Biết khối lượng và điện tích của electron lần lượt là 9,1.10-31 kg và -1,6.10-19 C.
Ta có, hạt chuyển động nhanh dần đều
Theo định luật II - Newton, ta có:
\(F = ma = \left| e \right|E \to a = \frac{{\left| e \right|E}}{m} = \frac{{1,{{6.10}^{ - 19}}.9,1}}{{9,{{1.10}^{ - 31}}}} = 1,{6.10^{12}}(m/{s^2})\)
+ Phương trình chuyển động của chùm electron:
\(s = {v_0}t + \frac{1}{2}a{t^2}\)
sau thời gian 1000ns chùm electron đi được quãng đường là:
\(s = {10^6}({1000.10^{ - 9}}) + \frac{1}{2}(1,{6.10^{12}}){({1000.10^{ - 9}})^2} = 1,8m\)
Hai bản kim loại phẳng có độ dài 30cm đặt nằm ngang, song song cách nhau một khoảng 16cm. Giữa hai bản tụ có một hiệu điện thế 4,55 V. Hướng một chùm hẹp các electron quang điện có tốc độ 106 (m/s) theo phương ngang vào giữa hai bản tại điểm O cách đều hai bản. Khối lượng của electron là 9,1.10-31 kg. Tính thời gian electron chuyển động trong tụ?
Theo định luật II - Newton, ta có:
\(F = ma = \left| e \right|E \to a = \frac{{\left| e \right|E}}{m} = \frac{{\left| e \right|U}}{{m{\rm{d}}}} = \frac{{1,{{6.10}^{ - 19}}.4,55}}{{9,{{1.10}^{ - 31}}.0,16}} = {5.10^{12}}(m/{s^2})\)
Gọi t1 là thời gian electron ra khỏi tụ điện:
\(0,3 = {10^6}{t_1} \to {t_1} = {3.10^{ - 7}}(s)\)
h - khoảng cách từ electron đến bản tụ:
\(h = \frac{{16}}{2} = 8cm\)
Gọi t2 là thời gian electron tới bản dương:
\({t_2} = \sqrt {\frac{{2h}}{a}} = \sqrt {\frac{{2.\frac{{0,16}}{2}}}{{{{5.10}^{12}}}}} \approx 1,{79.10^{ - 7}}(s)\)
Ta thấy t2 < t1 => electron chưa kịp ra khỏi bản tụ mà đã tới đập vào bản dương
=> Tính thời gian electron chuyển động trong tụ chính là
\({t_2} = {\rm{ }}1,{79.10^{ - 7}}\left( s \right)\)
Hai bản kim loại phẳng đặt nằm ngang, đối diện, song song cách nhau một khoảng d tạo thành một tụ điện phẳng. Giữa hai bản tụ có một hiệu điện thế U. Hướng một chùm hẹp các electron quang điện có tốc độ v theo phương ngang đi vào giữa hai bản tại điểm O cách đều hai bản thì khi nó vừa ra khỏi hai bản nó có tốc độ 2v. Khi vừa ra khỏi tụ điện, véctơ vận tốc hợp với véctơ vận tốc ban đầu một góc bằng bao nhiêu?
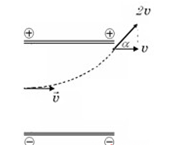
Từ hình, ta có:
\({\rm{cos}}\alpha = \frac{v}{{2v}} = \frac{1}{2} \to \alpha = {60^0}\)
Hai bản cực A, B của một tụ điện phẳng rất rộng làm bằng kim loại đặt song song và đối diện nhau, Khoảng cách giữa hai bản là 4cm. Chiếu vào tâm O của bản A một bức xạ đơn sắc thì tốc độ ban đầu cực đại của các electron quang điện là 0,76.106 (m/s). Khối lượng và điện tích của electron là 9,1.1031 kg và -1,6.10-19C. Đặt giữa hai bản A và B một hiệu điện thế UAB = 4,55 (V). Các electron quang điện có thể tới cách bản B một đoạn gần nhất là bao nhiêu?
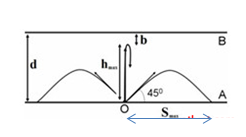
Theo định luật II - Newton, ta có:
\(F = ma = \left| e \right|E \to a = \frac{{\left| e \right|E}}{m} = \frac{{\left| e \right|U}}{{m{\rm{d}}}} = \frac{{1,{{6.10}^{ - 19}}.4,55}}{{9,{{1.10}^{ - 31}}.0,04}} = {2.10^{13}}(m/{s^2})\)
Độ cao cực đại:
\({h_{{\rm{max}}}} = \frac{{v_0^2}}{{2{\rm{a}}}} = \frac{{{{(0,{{76.10}^6})}^2}}}{{{{2.2.10}^{13}}}} = 0,01444m = 1,444cm\)
\( \to {b_{\min }} = d - {h_{{\rm{max}}}} = 4 - 1,444 = 2,556cm\)
Chiếu bức xạ thích hợp vào tâm của catốt của một tế bào quang điện thì tốc độ ban đầu cực đại của các electron quang điện là 7.105 (m/s). Đặt hiệu điện thế giữa anốt và catốt là UAK = 1V. Coi anốt và catốt là các bản phẳng rất rộng song song và cách nhau một khoảng 1cm. Khối lượng và điện tích của electron là 9,1.1031 kg và -1,6.10-19C. Tìm bán kính lớn nhất của miền trên anốt có electron quang điện đập vào?
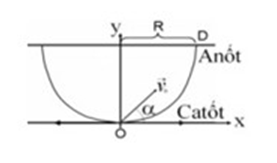
Theo định luật II - Newton, ta có:
\(F = ma = \left| e \right|E \to a = \frac{{\left| e \right|E}}{m} = \frac{{\left| e \right|U}}{{m{\rm{d}}}} = \frac{{1,{{6.10}^{ - 19}}.1}}{{9,{{1.10}^{ - 31}}.0,01}} = 1,{76.10^{13}}(m/{s^2})\)
Vì UAK > 0 nên anot hút các electron về phía nó. Những electron có vận tốc ban đầu cực đại bắn ra theo phương song song với hai bản sẽ ứng với Rmax
Phương trình chuyển động:
\(\left\{ \begin{array}{l}x = {v_0}t = R\\y = \frac{1}{2}a{t^2} = d\end{array} \right. \to \left\{ \begin{array}{l}t = \sqrt {\frac{{2{\rm{d}}}}{a}} \\R = {v_0}t = {v_0}\sqrt {\frac{{2{\rm{d}}}}{a}} \end{array} \right. \to R = {7.10^5}\sqrt {\frac{{2.0,01}}{{1,{{76.10}^{13}}}}} = 0,0236m \approx 2,4cm\)
Hai bản kim loại A và B phẳng rộng, đặt song song đối diện và cách nhau một khoảng d. Đặt vào A và B một hiệu điện thế UAB = U1 > 0. Sau đó chiếu vào tâm của tấm B một chùm sáng thì thấy xuất hiện các quang electron bay về phía tấm A. Tìm bán kính lớn nhất của vùng trên bề mặt anốt có electron đập vào. Biết rằng lúc này nếu đặt vào A và B một hiệu điện thế vừa đúng UAB = - U2 < 0 thì không còn electron nào đến được A.
Ta có:
+ \(\frac{{mv_0^2}}{2} = \left| e \right|{U_h} \to {v_0} = \sqrt {\frac{{2\left| e \right|{U_2}}}{m}} \)
+ gia tốc:
\(a = \frac{F}{m} = \frac{{\left| e \right|E}}{m} = \frac{{\left| e \right|{U_1}}}{{m{\rm{d}}}}\)
Khi
\(y = d \to t = \sqrt {\frac{{2{\rm{d}}}}{a}} = \sqrt {\frac{{2{\rm{d}}{\rm{.md}}}}{{\left| e \right|{U_1}}}} \)
+ Ta có:
\(R = {v_0}t = 2{\rm{d}}\sqrt {\frac{{{U_2}}}{{{U_1}}}} \)
Thiết lập hệ trục tọa độ đề các vuông góc Oxyz, trong một vùng không gian tồn tại một điện trường đều và một từ trường đều. Biết véctơ cường độ điện trường song song cùng chiều với Ox, véctơ cảm ứng từ song song cùng chiều với Oy. Cho một chùm hẹp các electron quang điện chuyển động vào không gian đó theo hướng Oz thì:
Ta có electron chịu tác dụng đồng thời hai lực:
+ Lực điện ngược hướng với Ox và có độ lớn:
\({F_d} = \left| e \right|E\)
+ Lực từ cùng hướng với Ox và có độ lớn:
\({F_L} = \left| e \right|{v_0}B\)
Hướng chùm electron quang điện có tốc độ 106 (m/s) vào một điện trường đều và một từ trường đều có cảm ứng từ 0,5.10-4 (T) thì nó vẫn chuyển động theo một đường thẳng. Biết véctơ \(\overrightarrow E \) song song cùng chiều với Ox, véctơ \(\overrightarrow B \) song song cùng chiều với Oy, véctơ vận tốc song song cùng chiều với Oz (Oxyz là hệ trục tọa độ đề các vuông góc). Độ lớn của véctơ cường độ điện trường là:
Ta có electron chịu tác dụng đồng thời hai lực:
+ Lực điện ngược hướng với Ox và có độ lớn:
\({F_d} = \left| e \right|E\)
+ Lực từ cùng hướng với Ox và có độ lớn:
\({F_L} = \left| e \right|{v_0}B\)
Vì electron chuyển động theo quỹ đạo thẳng nên lực điện và lực từ cân bằng nhau, ta có:
\(\left| e \right|E = \left| e \right|{v_0}B \to E = {v_0}B = {10^6}.0,{5.10^{ - 4}} = 50(V/m)\)
Chiếu bức xạ có bước sóng 0,5µm vào một tấm kim loại có công thoát 1,8 eV. Dùng màn chắn tách một chùm hẹp các electron quang điện và cho nó bay vào một điện trường từ A đến B sao cho UAB = − 10,8 V. Vận tốc nhỏ nhất và lớn nhất của electron khi tới B lần lượt là:
Khi chiếu bức xạ vào tấm kim loại, năng lượng của photon sẽ truyền cho electron để nó thoát khỏi lực liên kết với mạng tinh thể của kim loại, cung cấp động năng ban đầu và truyền 1 phần năng lượng cho mạng tinh thể. Với những electron ở ngay bề mặt kim loại, nó có thể thoát ra ngay và không mất năng lượng cho mạng tinh thể. Những electron này sẽ đạt được động năng cực đại (Wdmax = hc/λ – A). Ngược lại, những electron ở sâu bên trong kim loại, nó mất năng lượng truyền cho mạng tinh thể ; những electron nào dùng toàn bộ năng lượng để thoát khỏi lực liên kết và truyền năng lượng cho mạng tinh thể thì sẽ có động năng cực tiểu và bằng 0.
Ta có công
\(A' = {\rm{ }}q{U_{AB}}\;\) ;
công này dương, có tác dụng tăng tốc cho electron (vì điện tích của electron âm).
Mặt khác :
\(A' = {\rm{ }}{W_{dB}}--{\rm{ }}{W_{dA}} \Rightarrow {W_{dB}} = {\rm{ }}A{\rm{ }} + {\rm{ }}{W_{dA}}\;\;\;\;\;\;\;\;\;\left( 1 \right)\)
Electron có động năng cực đại
\({W_{dA}} = {\rm{ }}{W_{dmax}} = {\rm{ }}hc/\lambda --{\rm{ }}A\)
khi đến B sẽ đạt vận tốc lớn nhất.
Electron có động năng cực tiểu
\({W_{dA}} = {\rm{ }}0\) khi đến B sẽ đạt vận tốc nhỏ nhất.
Cực đại: từ (1)
\( \Rightarrow \frac{{mv_{\max }^2}}{2} = qU + \frac{{hc}}{\lambda } - A \Rightarrow {v_{\max }} = {2009.10^3}(m/s)\).
Cực tiểu: từ (1)
\( \Rightarrow \frac{{mv_{\min }^2}}{2} = qU \Rightarrow {v_{\min }} = {1949.10^3}(m/s)\).
Trong ống Cu-lít-giơ, electron của chùm tia catot khi đến anot (đối catot) có vận tốc cực đại là \(6,{6.10^7}m.{s^{ - 1}}\). Biết rằng năng lượng của mỗi phôtôn chùm tia X có được là nhờ sự chuyển hóa một phần động năng của electron. Lấy \({m_e} = {\rm{ }}9,{1.10^{ - 31}}kg\). Bước sóng ngắn nhất của tia X phát ra từ ống này là
Năng lượng của mỗi phôtôn chùm tia X có được là nhờ sự chuyển hóa một phần động năng của electron \( \Rightarrow \varepsilon \le {{\rm{W}}_{de}} \Leftrightarrow \dfrac{{hc}}{\lambda } \le \dfrac{{m{v^2}}}{2} \Rightarrow \lambda \ge \dfrac{{2hc}}{{m{v^2}}} = {10^{ - 10}}m = 0,1nm\)

