Ôn tập chương 6 - Lượng tử ánh sáng

+ Theo đề bài, khi xảy ra hiện tượng quang điện thì để triệt tiêu hoàn toàn dòng quang điện thì cần hiệu điện thế hãm U_h = 1,15 V

=> Động năng ban đầu cực đại của quang electron khi thoát ra khỏi bề mặt ca tốt là

Wđmax = e.U_h = 1,15 eV

+ Nếu ta đặt  vào hai đầu anôt và catôt một hiệu điện thế UAK = 4V

Theo định lí động năng ta có: ΔW_đ = A <=> W_đmax – W_đ0max = e.U_AK  = 4(eV)

=>  W_đmax = W_đ0max + e.U_AK = 1,15 + 4 = 5,15 (eV)

- Ta có: \({\lambda _0} = 300nm = {3.10^{ - 7}}m\)

- Áp dụng công thức tính công thoát: \(A{\rm{ }} = {\rm{ }}\dfrac{{h.c}}{{{\lambda _0}}} = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{3.10}^{ - 7}}}} = {6,625.10^{ - 19}}J = \dfrac{{{{6,625.10}^{ - 19}}}}{{{{1,6.10}^{ - 19}}}} = 4,14eV\)

A – sai vì các bức xạ trong dãy Passen mới thuộc vùng hồng ngoại

B – đúng vì các bức xạ của dãy Banme một phần nằm trong vùng ánh sáng nhìn thấy,một phần nằm trong vùng tử ngoại

C – sai vì các bức xạ trong dãy Lai man mới thuộc vùng tử ngoại

D – sai vì các bức xạ của dãy Banme một phần nằm trong vùng ánh sáng nhìn thấy,một phần nằm trong vùng tử ngoại

- Ta có: \(A{\rm{ }} = {\rm{ }}\dfrac{{h.c}}{{{\lambda _0}}} \to {\lambda _0} = \dfrac{{h.c}}{A} = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{6,625.1,6.10}^{ - 19}}}} = {0,1875.10^{ - 6}}m = 0,1875\mu m\)

- Điều kiện xảy ra hiện tượng quang điện là: \(\lambda  \le {\lambda _0} \to \) \({\lambda _1},{\lambda _3}\)gây ra được hiện tượng quang điện

- Sử dụng công thức Anhxtanh: \(\xi  = A + {{\rm{W}}_{od\max }} \to {{\rm{W}}_{od\max }} = \xi  - A\)

\( \to \) Động năng ban đầu cực đại của các e phụ thuộc vào năng lượng của photon chiếu tới và công thoát         

\( \to \) D đúng

- Ta có: \({\lambda _0} = 0,35\mu m\)

- Sử dụng điều kiện xảy ra hiện tượng quang điện là: \(\lambda  \le {\lambda _0}\)

\( \to \) hiện tượng quang điện sẽ không xảy ra với bước sóng là \(0,4\mu m\)

A,B,C – đúng

D – sai vì các photn bay dọc theo tia sáng với tốc độ \(c = {3.10^8}m/s\), tuy nhiên các photon tong các chùm sáng khác nhau có bước sóng khác nhau, dẫn tới năng lượng \(\xi  = \dfrac{{h.c}}{\lambda }\)là khác nhau

Ta có: \({n_e} = \dfrac{{{I_{bh}}}}{e} = \dfrac{{{{3.10}^{ - 3}}}}{{{{1,6.10}^{ - 19}}}} = {1,875.10^{16}}\)

A,B- sai vì quang phổ của nguyên tử H là quang phổ vạch, gồm 4 vạch màu đỏ, lam, chàm, tím

C- sai vì giữa các dãy Laiman, Banme, Passen có ranh giới xác định

D- đúng

\(\lambda  = 0,25\mu m = {0,25.10^{ - 6}}m\); \({\lambda _0} = 0,50\mu m = {0,5.10^{ - 6}}m\)

Ta có: \(\begin{array}{l}\xi  = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + \dfrac{1}{2}mv_{\max }^2\\ \to {v_{\max }} = \sqrt {\dfrac{{2.h.c}}{m}(\dfrac{1}{\lambda } - \dfrac{1}{{{\lambda _0}}})}  = \sqrt {\dfrac{{{{2.6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{9,1.10}^{ - 31}}}}(\dfrac{1}{{{{0,25.10}^{ - 6}}}} - \dfrac{1}{{{{0,5.10}^{ - 6}}}})}  = {9,34.10^5}m/s\end{array}\)

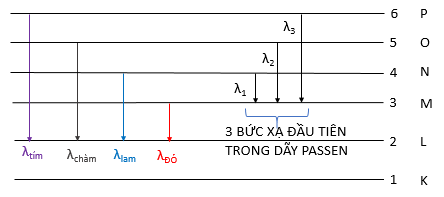
Thay \({\lambda _\alpha } = {\lambda _{do}};{\lambda _\beta } = {\lambda _{lam}} \to \dfrac{1}{{{\lambda _1}}} = \dfrac{1}{{{\lambda _\beta }}} - \dfrac{1}{{{\lambda _\alpha }}}\)

Ta có: \({\rm{\xi  = A + e}}{\rm{.}}{{\rm{U}}_h} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _o}}} + e.{U_h} \to {U_h} = \dfrac{{h.c}}{e}(\dfrac{1}{\lambda } - \dfrac{1}{{{\lambda _0}}}) = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{1,6.10}^{ - 19}}}}(\dfrac{1}{{{{320.10}^{ - 9}}}} - \dfrac{1}{{{{660.10}^{ - 9}}}}) = 2V\)

Ta có: Dãy Laiman trong quang phổ vạch của Hiđrô ứng với sự dịch chuyển của các electron từ các quỹ đạo dừng có năng lượng cao về quỹ đạo K

+ Theo công thức Anh - xtanh :

\({{hc} \over \lambda } = A + {1 \over 2}m.{v_0}^2 \Rightarrow {v_0}^2 = {2 \over m}\left( {{{hc} \over \lambda } - A} \right)\)  \(({m_e} = {9,1.10^{ - 31}}kg)\)

+ Ta có: \(a = {F \over m} = {{qE} \over m}\)

+ Chuyển động của e là chuyển động chậm dần đều với vận tốc đầu v₀ và gia tốc a

Electron dừng =>  v = 0 

\( \Leftrightarrow {0^2}-{\rm{ }}{v_0}^2 = {\rm{ }}2as \Rightarrow s =  - {{{v_0}^2} \over {2a}} =  - {{{2 \over m}\left( {{{hc} \over \lambda } - A} \right)} \over {2.{{qE} \over m}}} =  - {{{{hc} \over \lambda } - A} \over {qE}} \Rightarrow s = 0,109cm\)

- Ta có: \({n_e} = \dfrac{{{I_{bh}}}}{e} = \dfrac{{{{2.10}^{ - 6}}}}{{{{1,6.10}^{ - 19}}}} = {1,25.10^{13}}\)

- Lại có: \(H = \dfrac{{{n_e}}}{{{N_f}}}.100\%  \to {N_f} = \dfrac{{{{1,25.10}^{13}}.100\% }}{{0,5}} = {2,5.10^{15}}\)

- Ta có,

\(\begin{array}{l}\xi  = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + {{\rm{W}}_{od\max }}\\ \to {{\rm{W}}_{od\max }} = h.c.(\dfrac{1}{\lambda } - \dfrac{1}{{{\lambda _0}}}) = {6,625.10^{ - 34}}{.3.10^8}.(\dfrac{1}{{{{0,33.10}^{ - 6}}}} - \dfrac{1}{{{{0,66.10}^{ - 6}}}}) = {3,01.10^{ - 19}}J\end{array}\)

- Sử dụng định lí biến thiên động năng: \(\begin{array}{l}{{\rm{W}}_{dm{\rm{ax}}}} - {{\rm{W}}_{od\max }} = e.{U_{AK}}\\ \to {{\rm{W}}_{dm{\rm{ax}}}} = {{\rm{W}}_{od\max }} + e.{U_{AK}} = {3,01.10^{ - 19}} + {1,6.10^{ - 19}}.1,5 = {5,41.10^{ - 19}}J\end{array}\)

- Ta có,

\(\begin{array}{l}\xi  = A + {{\rm{W}}_{od\max }} \to \dfrac{{h.c}}{\lambda } = \dfrac{{h.c}}{{{\lambda _0}}} + {{\rm{W}}_{od\max }}\\ \to {{\rm{W}}_{od\max }} = h.c.(\dfrac{1}{\lambda } - \dfrac{1}{{{\lambda _0}}}) = {6,625.10^{ - 34}}{.3.10^8}.(\dfrac{1}{{{{0,2825.10}^{ - 6}}}} - \dfrac{1}{{{{0,66.10}^{ - 6}}}}) = {4,02.10^{ - 19}}J\end{array}\)

- Sử dụng định lí biến thiên động năng: \(\begin{array}{l}{{\rm{W}}_{dm{\rm{ax}}}} - {{\rm{W}}_{od\max }} = e.{U_{AK}}\\ \to {{\rm{W}}_{dm{\rm{ax}}}} = {{\rm{W}}_{od\max }} + e.{U_{AK}} = {4,02.10^{ - 19}} + {1,6.10^{ - 19}}.1,5 = {6,42.10^{ - 19}}J\end{array}\)

- Ta có: \({n_e} = \dfrac{{{I_{bh}}}}{e} = \dfrac{{{{2.10}^{ - 3}}}}{{{{1,6.10}^{ - 19}}}} = {1,25.10^{16}}\)

\({n_f} = \dfrac{P}{\xi } = \dfrac{P}{{\dfrac{{hc}}{\lambda }}} = \dfrac{{1,515}}{{\dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{546.10}^{ - 9}}}}}} = {4,16.10^{18}}\)

\( \to H = \dfrac{{{n_e}}}{{{N_f}}}.100\%  = \dfrac{{{{1,25.10}^{16}}}}{{{{4,16.10}^{18}}}} = {30.10^{ - 2}}\% \)

Ta có: \(\Delta {\rm{W  =  }}\dfrac{{hc}}{{{\lambda _0}}} \to {\lambda _0} = \dfrac{{hc}}{{\Delta {\rm{W}}}} = \dfrac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{2,2.1,6.10}^{ - 19}}}} = {5,6.10^{ - 7}}m = 0,56\mu m\)

Ta có:

\(\begin{array}{l}\xi  = A + e.{U_h}\\ \to {\xi _1} = A + e.{U_{h1}};{\xi _2} = A + e.{U_{h2}}\end{array}\)

Vì \({U_{h1}} = 2{U_{h2}} \to {\xi _1} > {\xi _2}\)

Lại có: \(\xi  = \dfrac{{h.c}}{\lambda }\)

\( \to {\lambda _1} < {\lambda _2}\)