Bài tập về phương trình sóng cơ tại một điểm trong trường giao thoa

+ Vì parabol đi qua hai nguồn A,B nên số điểm có biên độ bằng \(5mm\) nằm trên parabol không phụ thuộc vào vị trí đỉnh của parabol.

Số điểm có biên độ bằng \(5mm\) nằm trên parabol bằng hai lần số điểm có biên độ bằng \(5mm\) nằm trên đường thẳng nối hai nguồn.

+ Phương trình sóng do nguồn A gây ra tại M, nằm trên đường thẳng chứa hai nguồn có dạng :

\({u_{AM}} = 3cos(50\pi t + \dfrac{{2\pi d}}{\lambda })\)

+ Phương trình sóng do nguồn B gây ra tại  M, nằm trên đường thẳng chứa hai nguồn có dạng :

\({u_{BM}} = 4\cos (50\pi t + \dfrac{{2\pi (l - d)}}{\lambda })\)

+ Phương trình sóng do nguồn A,B gây ra tại điểm M :

\({u_M} = 3\cos (50\pi t + \dfrac{{2\pi d}}{\lambda }) + 4\cos (50\pi t + \dfrac{{2\pi (l - d)}}{\lambda }) = acos\left( {50\pi t + \varphi } \right)\)

Với : \(a = \sqrt {{3^2} + {4^2} + 2.3.4.c{\rm{os}}(\dfrac{{2\pi (l - d)}}{\lambda } - \dfrac{{2\pi d}}{\lambda }} )\)   (áp dụng công thức trong tổng hợp DĐĐH)

Để \(a{\rm{ }} = {\rm{ }}5mm\) thì : \(c{\rm{os}}(\dfrac{{2\pi (l - d)}}{\lambda } - \dfrac{{2\pi d}}{\lambda }) = 0 \to \dfrac{{2\pi (l - d)}}{\lambda } - \dfrac{{2\pi d}}{\lambda } = \left( {2k + 1} \right)\dfrac{\pi }{2}\) (1)

+ Ta có:

- Bước sóng: \(\lambda  = vT = v.\dfrac{{2\pi }}{\omega } = 30.\dfrac{{2\pi }}{{50}} = 1,2cm = 12mm\)

\(l = 12cm = 120mm\)

Từ (1), ta suy ra:

\(\begin{array}{l}\dfrac{{2\pi \left( {120 - d} \right)}}{{12}} - \dfrac{{2\pi d}}{{12}} = \left( {2k + 1} \right)\dfrac{\pi }{2}\\ \leftrightarrow 20 - \dfrac{d}{3} = \dfrac{{\left( {2k + 1} \right)}}{2}\\ \to d = \dfrac{{117}}{2} - 3k\end{array}\)

Lại có:  \(0 < d < 120mm\)

\(\begin{array}{l}0 < d = \dfrac{{117}}{2} - 3k < 120mm\\ \to  - 20,5 < k < 19,5\end{array}\)

=> Có 40 giá trị của k

Tức là có 40 điểm có biên độ bằng 5mm.

Do đó trên đường parabol trên có 80 điểm có biên độ bằng 5mm.

+ Tần số sóng: \(f = \frac{\omega }{{2\pi }} = \frac{{50\pi }}{{2\pi }} = 25Hz\)

+ Bước sóng \(\lambda  = \frac{v}{f} = \frac{{40}}{{25}} = 1,6cm\)

+ Xét điểm M trên \({S_1}{S_2}\): S₁M = d  (\(0 < d < 12cm\))

\({u_{{S_{1M}}}} = 6cos(50\pi t - \frac{{2\pi d}}{\lambda }){\rm{ }}mm = 6cos(50\pi t - \frac{{5\pi d}}{4})mm\)

\({u_{{S_{2M}}}} = 8cos(50\pi t - \frac{{2\pi (12 - d)}}{\lambda })mm\)

\( = 8cos(50\pi t + \frac{{2\pi d}}{\lambda } - \frac{{24\pi }}{\lambda })mm\)

\( = 8cos(50\pi t + \frac{{5\pi d}}{4} - 15\pi )\) mm

\( = 8cos\left( {50\pi t + \frac{{5\pi d}}{4} - \pi } \right)mm\)

+ Điểm M dao động với biên độ \(1{\rm{ }}cm = 10{\rm{ }}mm\) khi \({u_{S1M}}\) và \({u_{S2M}}\) vuông pha với nhau:

Ta có, độ lệch pha:

\(\begin{array}{l}\Delta \varphi  = \left( {\frac{{5\pi d}}{4} - \pi } \right) - \left( { - \frac{{5\pi d}}{4}} \right) = \frac{3\pi }{2} + k\pi \\ \leftrightarrow \frac{{5\pi d}}{2} = \frac{{3\pi }}{2} + k\pi \\ \to d = \frac{3}{5} + \frac{{2k}}{5}\end{array}\)

+ Mà 

\(\begin{array}{l}0 < d = \frac{3}{5} + \frac{{2k}}{5} < 12cm\\ \leftrightarrow  - 1,5 < k < 28,5\end{array}\)

=> Có \(30\) giá trị của \(k\)

Số điểm dao động với biên độ \(1cm\) trên đoạn thẳng S₁S₂ là \(30\)

Bước sóng: \(\lambda {\rm{}} = \frac{v}{f} = \frac{{120}}{{40}} = 3cm\)

Số điểm dao động cực đại trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thỏa mãn:

\({ - \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Leftrightarrow {\rm{}} - \frac{{20}}{3} < k < \frac{{20}}{3}}\)

\({ \Leftrightarrow {\rm{}} - 6,7 < k < 6,7 \Rightarrow k = {\rm{}} - 6; - 5;...;6}\)

Để khoảng cách giữa M và đường trung trực max thì M thuộc cực đại ứng với \({k_{max}} = 6\)

\({d_2} - {d_1} = {k_{\max }}\lambda {\rm{}} \Leftrightarrow MB - MA = 6.3 = 18cm\)

Mà \(MA = AB = 20cm \Rightarrow MB = 38cm\)

Ta có hình vẽ:

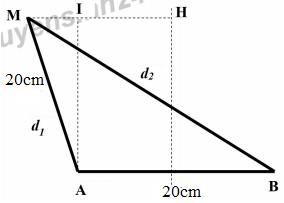
Áp dụng định lí hàm số cos trong tam giác MAB ta có:

\(\begin{array}{*{20}{l}}\begin{array}{l}M{B^2} = M{A^2} + A{B^2} - 2.MA.AB.cos\widehat {MAB}\\ \Rightarrow cos\widehat {MAB} = \frac{{M{A^2} + A{B^2} - M{B^2}}}{{2.MA.AB}} = \frac{{{{20}^2} + {{20}^2} - {{38}^2}}}{{2.20.20}}\\ \Rightarrow cos\widehat {MAB} =  - 0,805 \Rightarrow \widehat {MAB} = 143,{6^0}\end{array}\\{ \Rightarrow \widehat {MAI} = \widehat {MAB} - {{90}^0} = 53,{6^0}}\\{ \Rightarrow MI = AB.\sin \widehat {MAI} = 20.0,805 = 16,1cm}\\{ \Rightarrow b = MH = MI + IH = 16,1 + 10 = 26,1cm}\end{array}\)

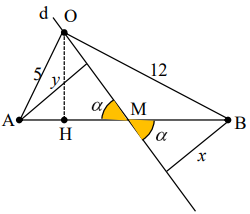
Ta có:

\(\left\{ \begin{array}{l}y = AM.\sin \alpha \\x = BM.\sin \alpha \end{array} \right. \Rightarrow x + y = \left( {AM + BM} \right).\sin \alpha  = 13.\sin \alpha \)

\({\left( {x + y} \right)_{\max }} = 13 \Leftrightarrow \sin \alpha  = 1 \Leftrightarrow \alpha  = {90^0}\)

Vậy \(M \equiv H\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{HA = \frac{{25}}{{13}}cm}\\
{HB = \frac{{144}}{{13}}cm}
\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{OA - OB = k\lambda }\\
{HA - HB = m\lambda }
\end{array}} \right.\)

\(\begin{array}{l}
\frac{k}{m} = \frac{{OA - OB}}{{HA - HB}} = \frac{{5 - 12}}{{\frac{{25}}{{13}} - \frac{{144}}{{13}}}} = \frac{{13}}{{17}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{k = - 13}\\
{m = - 17}
\end{array}} \right.\\
\Rightarrow OA - OB = 5 - 12 = - 13\lambda \Rightarrow \lambda = \frac{7}{{13}}cm
\end{array}\)

Số cực đại giao thoa trên \(AB\) bằng số giá trị \(n\) nguyên thỏa mãn:

\(\begin{array}{l} - \dfrac{{AB}}{\lambda } < n < \dfrac{{AB}}{\lambda } \Leftrightarrow  - \dfrac{{13}}{{\dfrac{7}{{13}}}} < k < \dfrac{{13}}{{\dfrac{7}{{13}}}}\\ \Leftrightarrow  - 24,1 < k < 24,1 \Rightarrow k =  - 24; - 23;...;24\end{array}\)

Có \(49\) giá trị của \(n,\) vậy có \(49\) điểm dao động với biên độ cực đại.

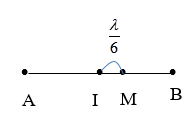
Xét điểm M trên AB; \(AM{\rm{ }} = {\rm{ }}{d_1};{\rm{ }}BM{\rm{ }} = {\rm{ }}{d_2}\) \(\left( {{\rm{ }}{d_1} > {d_2}} \right)\)

Sóng truyền từ A , B đến M

 \(\begin{array}{l}{u_{AM}} = acos(\omega t - \dfrac{{2\pi {d_1}}}{\lambda })\\{u_{BM}} = acos(\omega t - \dfrac{{2\pi {d_2}}}{\lambda } + \varphi )\\{u_M} = 2acos(\dfrac{{\pi ({d_1} - {d_2})}}{\lambda } + \dfrac{\varphi }{2})cos(\omega t - \dfrac{{\pi ({d_2} + {d_1})}}{\lambda } + \dfrac{\varphi }{2})\end{array}\)

 Điểm M không dao động khi: \(cos(\dfrac{{\pi ({d_1} - {d_2})}}{\lambda } + \dfrac{\varphi }{2}) = 0\)

 \(\dfrac{{\pi ({d_1} - {d_2})}}{\lambda } + \dfrac{\varphi }{2} = \dfrac{\pi }{2} + k\pi  \to {d_1}-{d_2} = (\dfrac{1}{2} - \dfrac{\varphi }{{2\pi }} + k)\lambda \)

Điểm M gần trung điểm I nhất ứng với (trường hợp hình vẽ)  \(k{\rm{ }} = {\rm{ }}0\)

Ta có: \(d_1-d_2=2MI=2\dfrac{\lambda}{6}=\dfrac{\lambda}{3}\)

Suy ra:

\(\begin{array}{l}\left( {\dfrac{1}{2} - \dfrac{\varphi }{{2\pi }}} \right)\lambda  = \dfrac{\lambda }{3}\\ \Rightarrow \dfrac{1}{2} - \dfrac{\varphi }{{2\pi }} = \dfrac{1}{3}\\ \Rightarrow \varphi  = \dfrac{{\pi }}{3}\end{array}\).

Ta có: \(A = 2{\rm{a}}\left| {{\rm{cos}}\left( {\frac{{\Delta \varphi }}{2} - \pi \frac{{\Delta d}}{\lambda }} \right)} \right|\)

Vì M và N là hai điểm cực đại nên ta có: \(\left\{ \begin{array}{l}\frac{{\Delta \varphi }}{2} - \pi \frac{{\Delta {d_M}}}{\lambda } = k\pi \\\frac{{\Delta \varphi }}{2} - \pi \frac{{\Delta {d_N}}}{\lambda } = (9 + k)\pi \end{array} \right.{\rm{             }}\left( 1 \right)\)

Mặt khác, ta có trên AB có 10 cực đại mà M và N là 2 cực đại gần A và B nhất và khoảng cách giữa 10 cực đại là \(\frac{{9\lambda }}{2}\)

Ta suy ra: \(MN = \frac{{9\lambda }}{2} \leftrightarrow AB - \left( {MA + NB} \right) = \frac{{9\lambda }}{2} \leftrightarrow 29 - \left( {1,5 + 0,5} \right) = \frac{{9\lambda }}{2} \to \lambda  = 6cm\)

Thay vào (1) ta được: \(\frac{{\Delta \varphi }}{2} = \pi \frac{{BM - AM}}{\lambda } + k\pi  = \frac{{13}}{3}\pi  + k\pi \)  

Do đó biên độ của điểm trên đường trung trực của AB là: \(A = 2{\rm{a}}\left| {{\rm{cos}}\left( {\frac{{\Delta \varphi }}{2}} \right)} \right| = 2.4\left| {{\rm{cos}}\left( {\frac{{13}}{3}\pi  + k\pi } \right)} \right| = 4cm\)

\(MN = 7\lambda  + \dfrac{{3\lambda }}{4}\) suy ra xét điểm N’ gần M nhất và \(MN' = \dfrac{{3\lambda }}{4}\)

+ Vậy hai điểm M và N luôn dao động vuông pha với nhau.

+ Bài toán sóng truyền trên nước có phương trình: \(u(t) = {u_0}\cos (2\pi ft - \dfrac{{2\pi x}}{\lambda })\)  nên biên độ sóng tại các điểm M và N một lúc nào đó sẽ bằng \({u_0}\)

+ Tại thời điểm t: \({u_M} = 6mm;{u_N} =  - 8m\)

Do M và N dao động vuông pha với nhau nên ta có: \({\left( {\dfrac{{{u_M}}}{{{u_0}}}} \right)^2} + {\left( {\dfrac{{{u_N}}}{{{u_0}}}} \right)^2} = 1\)

\( \to {u_0} = \sqrt {u_M^2 + u_N^2}  = \sqrt {{6^2} + {{\left( { - 8} \right)}^2}}  = 10mm\)

+ Do sóng truyền theo 1 chiều nhất định nên hai điểm M và N’ sẽ lệch pha nhau

\(t = \dfrac{{3\lambda }}{{4v}} \\\Rightarrow \varphi  = \omega t = \omega \dfrac{{3\lambda }}{{4v}} = \dfrac{{2\pi 3\lambda }}{{4Tv}} = \dfrac{{3\pi }}{2}\)

Vậy điểm M ở dưới tại thời điểm t và căn cứ như vậy theo chiều dương thì điểm N có pha nhanh hơn điểm N là \(\dfrac{{3\pi }}{2}\) nên sóng phải truyền từ N đến M.

+ Gọi x là khoảng cách từ điểm khảo sát (M) đến điểm H ( HB =  HA = d; và MB< MA)

Phương trình sóng tại M do sóng từ A truyền tới:

\({u_{AM}} = 4c{\rm{os}}\left( {10\pi \left( {t - \dfrac{{d + x}}{v}} \right)} \right) = 4c{\rm{os}}\left( {10\pi t - 10\pi \dfrac{{d + x}}{v}} \right)\)

Phương trình sóng tại M do sóng từ B truyền tới:

\({u_{BM}} = 4c{\rm{os}}\left( {10\pi \left( {t - \dfrac{{d - x}}{v}} \right) + \dfrac{\pi }{2}} \right) = 4c{\rm{os}}\left( {10\pi t - 10\pi \dfrac{{d - x}}{v} + \dfrac{\pi }{2}} \right)\)

Để sóng tại điểm M đứng yên thì 2 sóng truyền tới M phải ngược pha nhau

Do vậy ta có:

\(\begin{array}{l} - 10\pi \dfrac{{d - x}}{v} + \dfrac{\pi }{2} - \left( { - 10\pi \dfrac{{d + x}}{v}} \right) = \left( {2k + 1} \right)\pi \\ \leftrightarrow 10\pi \left( {\dfrac{{d + x}}{v} - \dfrac{{d - x}}{v}} \right) + \dfrac{\pi }{2} = \left( {2k + 1} \right)\pi \\ \to 20\dfrac{x}{v} = 2k + \dfrac{1}{2}\end{array}\)

Thay \(v{\rm{ }} = {\rm{ }}30{\rm{ }}cm/s\) ta có phương trình:

\(\begin{array}{l}20\dfrac{x}{{30}} = 2k + \dfrac{1}{2}\\ \to x = 3k + \dfrac{3}{4}\end{array}\)

Để\({x_{min}}\)  thì \(k{\rm{ }} = {\rm{ }}0\) ta có: \({x_{\min }} = \dfrac{3}{4} = 0,75cm\)

Do \(x \le \dfrac{{AB}}{2} = \dfrac{{25}}{2}\) ta có: \(3k + \dfrac{3}{4} \le \dfrac{{25}}{2} \to k \le 3,92\)

Suy ra để x_max thì \(k{\rm{ }} = {\rm{ }}3\)
Với \(k{\rm{ }} = {\rm{ }}3\) ta có: \({x_{max}} = 3.3 + \dfrac{3}{4} = 9,75cm\)

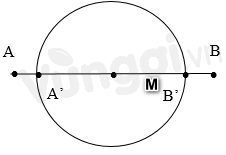
+ Bước sóng \(\lambda  = \dfrac{v}{f} = \dfrac{v}{{\dfrac{\omega }{{2\pi }}}} = \dfrac{{75}}{{\dfrac{{50\pi }}{{2\pi }}}} = 3cm\)

+ Xét điểm M trên \(A'B'\):  \(\begin{array}{l}{d_1} = {\rm{ }}AM\\{d_2} = {\rm{ }}BM\end{array}\)

Sóng truyền từ A, B đến M:

\({u_{AM}} = 6cos(50\pi t + \dfrac{\pi }{3} - \dfrac{{2\pi {d_1}}}{\lambda }) = 6cos(50\pi t + \dfrac{\pi }{3} - \dfrac{{2\pi {d_1}}}{3}){\rm{            (1)}}\)

\({u_{BM}} = 8cos(50\pi t + \dfrac{{5\pi }}{6} - \dfrac{{2\pi {d_2}}}{\lambda })\)

\( = 8cos\left( {50\pi t + \dfrac{{5\pi }}{6} - \dfrac{{2\pi (12 - {d_1})}}{3}} \right)\)

\( = 8cos(50\pi t + \dfrac{{5\pi }}{6} + \dfrac{{2\pi {d_1}}}{3} - 8\pi )\)

\( = 8cos(10\pi t + \dfrac{{5\pi }}{6} + \dfrac{{2\pi {d_1}}}{3})\)          (2)

\({u_M} = {\rm{ }}{u_{AM}} + {\rm{ }}{u_{BM}}\) có biên độ bằng \(10{\rm{ }}cm\) khi \({u_{AM}}\) và \({u_{BM}}\) vuông pha với nhau:

\(\begin{array}{l}\dfrac{{5\pi }}{6} + \dfrac{{2\pi {d_1}}}{3} - \left( {\dfrac{\pi }{3} - \dfrac{{2\pi {d_1}}}{3}} \right) = \dfrac{\pi }{2} + k\pi \\ \leftrightarrow \dfrac{\pi }{2} + \dfrac{{4\pi {d_1}}}{3} = \dfrac{\pi }{2} + k\pi \\ \to {d_1} = \dfrac{{3k}}{4}\end{array}\)

Mặt khác, ta có: 

\(AA' \le {d_1} \le AB'\) => \(\begin{array}{l}2 \le {d_1} = \dfrac{{3k}}{4} \le 10\\ \to \dfrac{8}{3} \le k \le \dfrac{{40}}{3}\\ \to k = 3,4,5,6,7,8,9,10,11,12,13\end{array}\)

Như vậy trên A’B’ có  11  điểm dao động với biên độ \(10{\rm{ }}cm\)

Suy ra trên đường tròn tâm O bán kính \(R = 4cm\) có 22 điểm dao động với biên độ \(10 cm\)

Do đó trên đường tròn có \(22\) điểm dao động với biện độ \(10 cm\).

Bài cho hai nguồn dao động vuông  pha (\(\Delta \varphi  = {\varphi _2} - {\varphi _1} = \pi  - \frac{\pi }{2} = \frac{\pi }{2}\)) nên các điểm thuộc mặt nước nằm trên đường trung trực của AB sẽ dao động với biên độ \(a = 2a\left| {c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{4}} \right)} \right| = 2.3c{\rm{os}}\frac{\pi }{4} = 3\sqrt 2 cm\)

(vì lúc này \({d_1} = {d_2}\))

Theo giả thiết nhìn vào phương trình sóng ta thấy hai nguồn dao động ngược pha nên tại O là trung điểm của AB sẽ dao động với biên độ cực tiểu \({a_M} = 0\)

+ Bước sóng: \(\lambda  = \frac{v}{f} = \frac{{60}}{{15}} = 4cm\)

Cách 1:

+ Ta có biên độ dao động tại điểm M trong trường giao thoa với hai nguồn ngược pha:

\({a_M} = 2A\left| {c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)} \right| = 6\left| {c{\rm{os}}\left( {\pi \frac{{AM - BM}}{\lambda } + \frac{\pi }{2}} \right)} \right| = 6\left| {c{\rm{os}}\left( {\pi \frac{{12 - 10}}{4} + \frac{\pi }{2}} \right)} \right| = 6cm\)

Cách 2:

Ta thấy: \(AM - BM = 2cm = \left( {k + \frac{1}{2}} \right)\lambda \) (với k = 0)

Hai nguồn ngược pha nên điểm M dao động cực đại

Þ Biên độ dao động tổng hợp tại M: a = 6cm

Cách 1:

+ Bước sóng: \(\lambda  = \frac{v}{f} = \frac{{120}}{{\frac{{50\pi }}{{2\pi }}}} = 4,8cm\)

+ Ta có biên độ dao động tại một điểm bất kì trong trường giao thoa:

\(a = 2A\left| {c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)} \right| = 10c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)\)

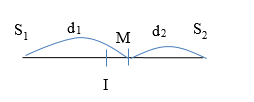
Ta có: \({d_2} - {\rm{ }}{d_1} = {\rm{ }}2MI{\rm{ }} = {\rm{ }}6cm\)

\( \to {a_M} = 10\left| {c{\rm{os}}\left( {\pi \frac{6}{{4,6}} + \frac{\pi }{2}} \right)} \right| = 10\left| {cos\left( {\frac{{7\pi }}{4}} \right)} \right| = 5\sqrt 2 mm\)

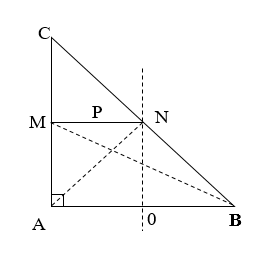
+ Bước sóng: \(\lambda  = vT = v.\frac{{2\pi }}{\omega } = 30.\frac{{2\pi }}{{30\pi }} = 2cm\)

+ Phương trình sóng tại 1 điểm P trên MN:

\({u_{{P_1}}} = 6cos\left( {30\pi t + \frac{\pi }{6} - \frac{{2\pi {d_1}}}{\lambda }} \right)\left( {mm;s} \right)\)

\({u_{{P_2}}} = 8cos\left( {30\pi t - \frac{\pi }{2} - \frac{{2\pi {d_2}}}{\lambda }} \right)\left( {mm;s} \right)\)

Độ lệch pha: \(\Delta \varphi  = \frac{\pi }{6} - \frac{{2\pi {d_1}}}{\lambda } - \left( { - \frac{\pi }{2} - \frac{{2\pi {d_2}}}{\lambda }} \right) = \frac{{2\pi }}{3} + \frac{{2\pi \left( {{d_2} - {d_1}} \right)}}{\lambda }\)

+ Khi \({A_P} = 2mm{\rm{ }} = {\rm{ }}{A_2}-{\rm{ }}{A_1}\) => P trên cực tiểu giao thoa.

\(\begin{array}{l} \to \Delta \varphi  = \pi  + k2\pi \\ \to \frac{{2\pi }}{3} + \frac{{2\pi \left( {{d_2} - {d_1}} \right)}}{\lambda } = \pi  + k2\pi \\ \leftrightarrow \frac{2}{3} + \left( {{d_2} - {d_1}} \right) = 1 + 2k\\ \to \left( {{d_2} - {d_1}} \right) = \frac{1}{3} + 2k\end{array}\)

+ Ta có P trên MN nên :

\(NB - NA \le {d_2} - {d_1} \le MB - MA\)  (với \(MB = \sqrt {{{15}^2} + {{30}^2}}  = 15\sqrt 5 cm\))

\(\begin{array}{l} =  > {\rm{ }}0 \le \frac{1}{3} + 2k \le 15\sqrt 5  - 15\\ \to  - 0,167 \le k \le 9,1\\ \to k = 0,1,...,9\end{array}\)

=> 10 điểm

+ Bước sóng: \(\lambda  = \dfrac{v}{f} = \dfrac{v}{{\frac{\omega }{{2\pi }}}} = \dfrac{{40}}{{\dfrac{{50}}{{2\pi }}}} = 1,6cm\)

+ Hai nguồn cùng pha nên trung điểm I dao động cực đại: A_max = 6 + 8 = 14 mm

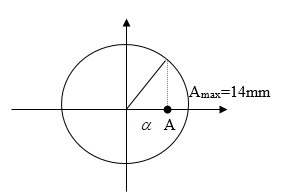
\(\cos \alpha  = \dfrac{A}{{{A_{\max }}}} = \dfrac{{10}}{{14}} \\\to \alpha  = 0,7751933733rad = \Delta \varphi \)

Độ lệch pha giữa I và M cần tìm là \(\Delta \varphi  = \dfrac{{2\pi }}{\lambda }d = 0,77519 \to d = 0,197cm\)

+ Bước sóng: \(\lambda  = vT = v.\dfrac{{2\pi }}{\omega } = 15.\dfrac{{2\pi }}{{40}} = 0,75cm\)

Hai nguồn giống nhau, nên:

Vì \({M_1}\) và \({M_2}\) nằm trên cùng một elip nên ta luôn có \(A{M_1} + {\rm{ }}B{M_1} = {\rm{ }}A{M_2} + {\rm{ }}B{M_2}\)

Tức là \({d_1} + {\rm{ }}{d_2} = {\rm{ }}d{'_1} + {\rm{ }}d{'_2}\)

\(\Delta {d_1} = {\rm{ }}{d_1}-{\rm{ }}{d_2} = A{M_1} - B{M_1} = 1\,cm\)

\(\begin{array}{l}{u_{{M_1}}} = 2.6\cos \pi \dfrac{{\Delta {d_1}}}{\lambda }\cos (\omega t - \pi \dfrac{{{d_1} + {d_2}}}{\lambda });\\{u_{{M_2}}} = 2.6\cos \pi \dfrac{{\Delta {d_2}}}{\lambda }\cos (\omega t - \pi \dfrac{{d{'_1} + d{'_2}}}{\lambda });\\{d_1} + {d_2} = d{'_1} + d{'_2}\\ \Rightarrow \dfrac{{{u_{M2}}}}{{{u_{M1}}}} = \dfrac{{\cos \pi \dfrac{{\Delta {d_2}}}{\lambda }}}{{\cos \pi \dfrac{{\Delta {d_1}}}{\lambda }}} = \dfrac{{c{\rm{os}}\dfrac{\pi }{\lambda }.3,5}}{{c{\rm{os}}\dfrac{\pi }{\lambda }.1}} = \dfrac{{c{\rm{os}}\dfrac{\pi }{{0,75}}(3 + \dfrac{1}{2})}}{{c{\rm{os}}\dfrac{\pi }{{0,75}}}} = \dfrac{{c{\rm{os}}(4\pi  + \dfrac{{2\pi }}{3})}}{{c{\rm{os}}\dfrac{{4\pi }}{3}}} = \dfrac{{c{\rm{os}}\dfrac{{2\pi }}{3}}}{{c{\rm{os}}\dfrac{{4\pi }}{3}}} = 1\\ \Rightarrow {u_{M2}} = {u_{M1}} = 3mm\end{array}\)

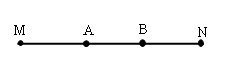
Ta có biên độ tại một điểm trong trường giao thoa:

\(a = 2A\left| {c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda }} \right)} \right|\)

Ta có : \(\left| {MA - MB} \right| = \left| {NA - NB} \right| = AB\)

=> \({a_M} = {a_N} = 4mm\)

Biên độ tổng hợp tại N có giá trị bằng biên độ dao động tổng hợp tại M và bằng \(4mm\).

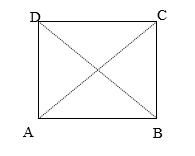
+ Bước sóng: \(\lambda  = \dfrac{v}{f} = \dfrac{{30}}{{30}} = 1cm\)

+  Phương trình giao thoa sóng: \({u_M} = 2{\rm{acos}}\left( {\pi \dfrac{{{d_2} - {d_1}}}{\lambda }} \right){\rm{cos}}\left( {\omega t - \pi \dfrac{{{d_1} + {d_2}}}{\lambda }} \right)\)

\(\begin{array}{l}{a_M} = a\sqrt 2  \\\to 2{\rm{acos}}\left( {\pi \dfrac{{{d_2} - {d_1}}}{\lambda }} \right) =   \pm a\sqrt 2  \\\to {\rm{cos}}\left( {\pi \dfrac{{{d_2} - {d_1}}}{\lambda }} \right) =  \pm \dfrac{{\sqrt 2 }}{2}\\ \to \pi \dfrac{{{d_2} - {d_1}}}{\lambda } = \dfrac{\pi }{4} + k\dfrac{\pi }{2} \\\to {d_2} - {d_1} = \left( {\dfrac{1}{4} + \dfrac{k}{2}} \right)\lambda \end{array}\)

+  M trên đoạn CD :

\(\begin{array}{l}CB-CA < {d_2}-{d_1} < DB-DA\\ \leftrightarrow 12 - 12\sqrt 2  \le \left( {\dfrac{1}{4} + \dfrac{k}{2}} \right)\lambda  \le 12\sqrt 2  - 12\\ \leftrightarrow  - 10,44 \le k \le 9,44\\ \to k =  - 10, \pm 9, \pm 8, \pm 7, \pm 6, \pm 5, \pm 4, \pm 3, \pm 2, \pm 1,0\end{array}\)

=> 20 điểm

Cách 1: Bước sóng λ = v/f = 2 cm.

Xét điểm M trên S₁S₂: S₁M  = d ( 0 < d < 8 cm)

\({u_{{S_{1M}}}} = 6cos(40\pi t - \dfrac{{2\pi d}}{\lambda }){\rm{ }}cm = 6cos(40\pi t - \pi d)cm\)

\({u_{{S_{2M}}}} = 8cos(40\pi t - \frac{{2\pi (8 - d)}}{\lambda })cm = 8cos(40\pi t + \frac{{2\pi d}}{\lambda } - \dfrac{{16\pi }}{\lambda })cm = 8cos(40\pi t + \pi d - 8\pi )cm\))

Điểm M dao động với biên độ 10 cm khi u_S1M và u_S2M vuông pha với nhau:

\(2\pi d = \dfrac{\pi }{2} + {\text{ }}k\pi \)

\( =  > d = \dfrac{1}{4} + \dfrac{k}{2}\) mà : \(0 < d = \dfrac{1}{4} + \dfrac{k}{2} < 8 \to  - {\text{ }}0,5 < k < 15,5 \to 0 \leqslant k \leqslant {\text{ }}15\)

=> Có 16 giá trị của k

Số điểm dao động với biên độ 1cm trên đoạn thẳng S₁S₂ là 16.

Cách 2: Cách khác nhanh hơn:

+ Số cực đại giữa hai nguồn

\( - \frac{{{S_1}{S_2}}}{\lambda } < k < \dfrac{{{S_1}{S_2}}}{\lambda } \leftrightarrow  - 4 < k < 4\).

Có 7 cực đại (Nếu hai nguồn tạm xem là 2 cực đại là thì là 9 cực đại, vì nguồn là cực đại hay cực tiểu đang gây tranh cãi)

+ Số cực tiểu giữa hai nguồn

\( - \dfrac{{{S_1}{S_2}}}{\lambda } - \dfrac{1}{2} < k < \dfrac{{{S_1}{S_2}}}{\lambda }\dfrac{1}{2} \leftrightarrow  - 4,5 < k < 3,5\).

Có 8 cực tiểu

+ Biên độ Cực đại: A­_max = 6 + 8 = 14cm

+ Biên độ cực tiểu: A_min = 8 - 6 = 2cm

+ Và giữa 1 cực đại và 1 cực tiểu có điểm dao động biên độ bằng 10mm. Theo đề bài giữa hai nguồn có 9 cực đại (tạm xem) với 8 cực tiểu \( \to \) có 17 vân cực trị nên có 16 vân biên độ 10cm.

+ Vì parabol đi qua hai nguồn A,B nên số điểm có biên độ bằng $5mm$ nằm trên parabol không phụ thuộc vào vị trí đỉnh của parabol. Số điểm có biên độ bằng $5mm$ nằm trên parabol bằng hai lần số điểm có biên độ bằng $5mm$ nằm trên đường thẳng nối hai nguồn.

+ Phương trình sóng do nguồn $A$ gây ra tại $M$, nằm trên đường thẳng chứa hai nguồn có dạng:

\({u_{AM}} = 3cos(40\pi t + \dfrac{{2\pi d}}{\lambda })\)

+ Phương trình sóng do nguồn $B$ gây ra tại  $M$, nằm trên đường thẳng chứa hai nguồn có dạng :

\({u_{BM}} = 4\cos (40\pi t + \dfrac{{2\pi (l - d)}}{\lambda })\)

+ Phương trình sóng do nguồn $A,B$ gây ra tại điểm $M$ :

\({u_M} = 3\cos (40\pi t + \dfrac{{2\pi d}}{\lambda }) + 4\cos (40\pi t + \dfrac{{2\pi (l - d)}}{\lambda }) = acos\left( {40\pi t + \varphi } \right)\)

Với : \(a = \sqrt {{3^2} + {4^2} + 2.3.4.c{\rm{os}}(\dfrac{{2\pi (l - d)}}{\lambda } - \dfrac{{2\pi d}}{\lambda }} )\)   (áp dụng công thức trong tổng hợp ddđh)

Để $a = 5mm$ thì : \(c{\rm{os}}(\dfrac{{2\pi (l - d)}}{\lambda } - \dfrac{{2\pi d}}{\lambda }) = 0 \to \dfrac{{2\pi (l - d)}}{\lambda } - \dfrac{{2\pi d}}{\lambda } = \left( {2k + 1} \right)\dfrac{\pi }{2}\)

Thay: \(\lambda =15mm\), $l = 100mm$ và: $0 < d < 100$

Ta được:  $ - 13,8 < k < 12,8$

=> Có \(26\) giá trị của k tức là có \(26\) điểm có biên độ bằng \(5mm\).

=> Do đó trên đường parabol trên có \(26.2 = 52\) điểm có biên độ bằng \(5mm\).