Ở mặt thoáng của một chất lỏng có hai nguồn kết hợp A, B cách nhau \(12cm\), dao động theo phương thẳng đứng với phương trình lần lượt là \({u_A} = 6cos\left( {50\pi t + \dfrac{\pi }{3}} \right)cm\); \({u_B} = 8cos\left( {50\pi t + \dfrac{{5\pi }}{6}} \right)cm\). Cho biết tốc độ truyền sóng là \(75cm/s\). Một đường tròn có tâm là trung điểm của AB, nằm trên mặt nước, có bán kính \(4cm\). Số điểm dao động với biên độ \(10cm\) có trên đường tròn là:
Trả lời bởi giáo viên
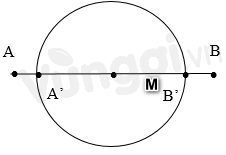
+ Bước sóng \(\lambda = \dfrac{v}{f} = \dfrac{v}{{\dfrac{\omega }{{2\pi }}}} = \dfrac{{75}}{{\dfrac{{50\pi }}{{2\pi }}}} = 3cm\)
+ Xét điểm M trên \(A'B'\): \(\begin{array}{l}{d_1} = {\rm{ }}AM\\{d_2} = {\rm{ }}BM\end{array}\)
Sóng truyền từ A, B đến M:
\({u_{AM}} = 6cos(50\pi t + \dfrac{\pi }{3} - \dfrac{{2\pi {d_1}}}{\lambda }) = 6cos(50\pi t + \dfrac{\pi }{3} - \dfrac{{2\pi {d_1}}}{3}){\rm{ (1)}}\)
\({u_{BM}} = 8cos(50\pi t + \dfrac{{5\pi }}{6} - \dfrac{{2\pi {d_2}}}{\lambda })\)
\( = 8cos\left( {50\pi t + \dfrac{{5\pi }}{6} - \dfrac{{2\pi (12 - {d_1})}}{3}} \right)\)
\( = 8cos(50\pi t + \dfrac{{5\pi }}{6} + \dfrac{{2\pi {d_1}}}{3} - 8\pi )\)
\( = 8cos(10\pi t + \dfrac{{5\pi }}{6} + \dfrac{{2\pi {d_1}}}{3})\) (2)
\({u_M} = {\rm{ }}{u_{AM}} + {\rm{ }}{u_{BM}}\) có biên độ bằng \(10{\rm{ }}cm\) khi \({u_{AM}}\) và \({u_{BM}}\) vuông pha với nhau:
\(\begin{array}{l}\dfrac{{5\pi }}{6} + \dfrac{{2\pi {d_1}}}{3} - \left( {\dfrac{\pi }{3} - \dfrac{{2\pi {d_1}}}{3}} \right) = \dfrac{\pi }{2} + k\pi \\ \leftrightarrow \dfrac{\pi }{2} + \dfrac{{4\pi {d_1}}}{3} = \dfrac{\pi }{2} + k\pi \\ \to {d_1} = \dfrac{{3k}}{4}\end{array}\)
Mặt khác, ta có:
\(AA' \le {d_1} \le AB'\) => \(\begin{array}{l}2 \le {d_1} = \dfrac{{3k}}{4} \le 10\\ \to \dfrac{8}{3} \le k \le \dfrac{{40}}{3}\\ \to k = 3,4,5,6,7,8,9,10,11,12,13\end{array}\)
Như vậy trên A’B’ có 11 điểm dao động với biên độ \(10{\rm{ }}cm\)
Suy ra trên đường tròn tâm O bán kính \(R = 4cm\) có 22 điểm dao động với biên độ \(10 cm\)
Do đó trên đường tròn có \(22\) điểm dao động với biện độ \(10 cm\).
Hướng dẫn giải:
- Áp dụng công thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
- Viết phương trình sóng tại 1 điểm bất kì trên A’B’

