Câu hỏi:
2 năm trước
Hai nguồn song kết hợp A và B dao động theo phương trình: uA=acosωt. và uB=acos(ωt+φ). Biết điểm không dao động gần trung điểm I của AB nhất một đoạn λ6.Tìm φ
Trả lời bởi giáo viên
Đáp án đúng: b
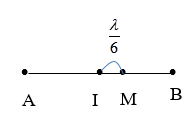
Xét điểm M trên AB; AM=d1;BM=d2 (d1>d2)
Sóng truyền từ A , B đến M
uAM=acos(ωt−2πd1λ)uBM=acos(ωt−2πd2λ+φ)uM=2acos(π(d1−d2)λ+φ2)cos(ωt−π(d2+d1)λ+φ2)
Điểm M không dao động khi: cos(π(d1−d2)λ+φ2)=0
π(d1−d2)λ+φ2=π2+kπ→d1−d2=(12−φ2π+k)λ
Điểm M gần trung điểm I nhất ứng với (trường hợp hình vẽ) k=0
Ta có: d1−d2=2MI=2λ6=λ3
Suy ra:
(12−φ2π)λ=λ3⇒12−φ2π=13⇒φ=π3.
Hướng dẫn giải:
+ Viết phương trình dao động tổng hợp tại một điểm trong trường giao thoa.
+ Điểm không dao động khi biên độ dao động tổng hợp tại điểm đó = 0

