Trên mặt nước tại hai điểm \({S_1},{\rm{ }}{S_2}\) người ta đặt hai nguồn sóng cơ kết hợp, dao động điều hoà theo phương thẳng đứng với phương trình \({u_A} = 6cos50\pi t\) và \({u_B} = 8cos50\pi t\) (\({u_A}\) và \({u_B}\) tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt nước là \(40cm/s\), coi biên độ sóng không đổi khi truyền đi. Trên đoạn thẳng \({S_1}{S_2}\), điểm dao động với biên độ \(1cm\) và cách trung điểm của đoạn \({S_1}{S_2}\) một đoạn gần nhất là:
Trả lời bởi giáo viên
+ Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{v}{{\frac{\omega }{{2\pi }}}} = \dfrac{{40}}{{\dfrac{{50}}{{2\pi }}}} = 1,6cm\)
+ Hai nguồn cùng pha nên trung điểm I dao động cực đại: Amax = 6 + 8 = 14 mm
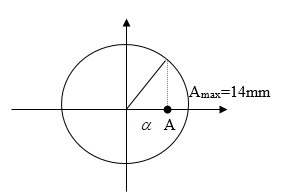
\(\cos \alpha = \dfrac{A}{{{A_{\max }}}} = \dfrac{{10}}{{14}} \\\to \alpha = 0,7751933733rad = \Delta \varphi \)
Độ lệch pha giữa I và M cần tìm là \(\Delta \varphi = \dfrac{{2\pi }}{\lambda }d = 0,77519 \to d = 0,197cm\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Sử dụng vòng tròn lượng giác và công thức: \(\Delta \varphi = \dfrac{{2\pi }}{\lambda }d\)

