Cho hai nguồn sóng kết hợp trên mặt nước trên mặt nước \({u_1} = 6cos\left( {30\pi t + \frac{\pi }{6}} \right)\left( {mm;s} \right)\) và \({u_2} = 8cos\left( {30\pi t - \frac{\pi }{2}} \right)\left( {mm;s} \right)\) tại hai điểm A và B cách nhau \(30{\rm{ }}cm\). Cho tốc độ truyền sóng trên mặt nước là \(30cm/s\); Coi biên độ sóng không đổi khi truyền đi. Điểm C trên mặt nước sao cho ABC là tam giác vuông cân đỉnh A. Số điểm dao động với biên độ \(2{\rm{ }}mm\) trên đường trung bình song song cạnh AB của tam giác ABC là:
Trả lời bởi giáo viên
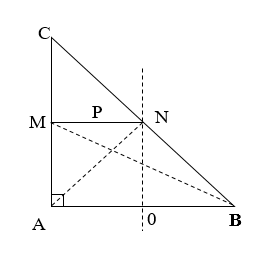
+ Bước sóng: \(\lambda = vT = v.\frac{{2\pi }}{\omega } = 30.\frac{{2\pi }}{{30\pi }} = 2cm\)
+ Phương trình sóng tại 1 điểm P trên MN:
\({u_{{P_1}}} = 6cos\left( {30\pi t + \frac{\pi }{6} - \frac{{2\pi {d_1}}}{\lambda }} \right)\left( {mm;s} \right)\)
\({u_{{P_2}}} = 8cos\left( {30\pi t - \frac{\pi }{2} - \frac{{2\pi {d_2}}}{\lambda }} \right)\left( {mm;s} \right)\)
Độ lệch pha: \(\Delta \varphi = \frac{\pi }{6} - \frac{{2\pi {d_1}}}{\lambda } - \left( { - \frac{\pi }{2} - \frac{{2\pi {d_2}}}{\lambda }} \right) = \frac{{2\pi }}{3} + \frac{{2\pi \left( {{d_2} - {d_1}} \right)}}{\lambda }\)
+ Khi \({A_P} = 2mm{\rm{ }} = {\rm{ }}{A_2}-{\rm{ }}{A_1}\) => P trên cực tiểu giao thoa.
\(\begin{array}{l} \to \Delta \varphi = \pi + k2\pi \\ \to \frac{{2\pi }}{3} + \frac{{2\pi \left( {{d_2} - {d_1}} \right)}}{\lambda } = \pi + k2\pi \\ \leftrightarrow \frac{2}{3} + \left( {{d_2} - {d_1}} \right) = 1 + 2k\\ \to \left( {{d_2} - {d_1}} \right) = \frac{1}{3} + 2k\end{array}\)
+ Ta có P trên MN nên :
\(NB - NA \le {d_2} - {d_1} \le MB - MA\) (với \(MB = \sqrt {{{15}^2} + {{30}^2}} = 15\sqrt 5 cm\))
\(\begin{array}{l} = > {\rm{ }}0 \le \frac{1}{3} + 2k \le 15\sqrt 5 - 15\\ \to - 0,167 \le k \le 9,1\\ \to k = 0,1,...,9\end{array}\)
=> 10 điểm
Hướng dẫn giải:
+ Viết phương trình sóng tại M
+ Sử dụng điều kiện biên độ
+ Xác định khoảng chạy của \({d_2} - {\rm{ }}{d_1}\)

