Đặt điện áp u = U0cosωt vào hai đầu đoạn mạch như hình bên. Biết tụ điện có điện dung C thay đổi được. Đồ thị hình bên mô tả số chỉ của vôn kế V1 và vôn kế V2 tương ứng là UV1 và UV2 phụ thuộc vào điện dung C. Biết U3 = 2U2. Tỉ số U2U4 là
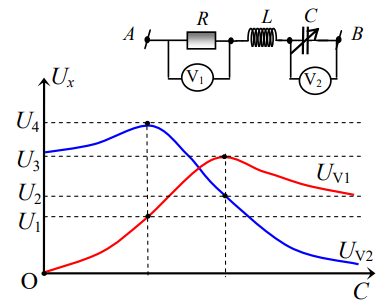

Từ đồ thị ta thấy khi ZC=ZC1 ⇒UV1max=U3=U → mạch có cộng hưởng: ZL = ZC1
Khi đó: UV2=UC=U2⇒UZC1R=U2
Ta có: U3=2U2⇒U=2U.ZC1R⇒R=2ZC1=2ZL
⇒U2=UZC1R=U.ZLR=U2
Khi ZC=ZC2⇒UV2max=UCmax=U4⇒U4=U√R2+ZL2R
⇒U4=U√R2+ZL2R=U.√4ZL2+ZL22ZL=U√52⇒U2U4=U2U√52=1√5
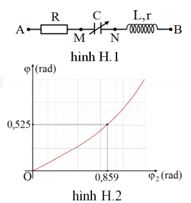
Đặt điện áp xoay chiều (có giá trị hiệu dụng và tần số không đổi) vào hai đầu đoạn mạch như hình H.1 thì cảm kháng của cuộn dây ZL=2r. Gọi φ và φ2 tương ứng là độ lệch pha giữa điện áp uAB và uMB so với cường độ dòng điện trong mạch. Đồ thị biểu diễn sự phụ thuộc của φ vào φ2 khi điện dung C thay đổi như hình H.2. Khi C=C0 thì điện áp uAN lệch pha 900 so với uMB. Khi đó, hệ số công suất của đoạn mạch MB là
Ta có: {tanφ=ZLCR+r=tan0,525tanφ2=ZLCr=tan0,859⇒R+rr=2⇒R=r
Lấy R=1=r⇒ZL=2
Theo bài ta có: uAN⊥uMB⇒ZC0R.ZL−ZC0r=1⇒ZC0=1.
Hệ số công suất của đoạn mạch MB là:
cosφMB=r√r2+(ZL−ZC0)2=1√2=0,71.
Mạch điện nối tiếp gồm điện trở R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C thay đổi được . Điện áp hai đầu là U ổn định, tần số f. Thay đổi C để UCmax. Chọn hệ thức sai?
Ta có C thay đổi để UC max, khi đó:UCmax=U2R+U2LUL=U√R2+Z2LR
{URL⊥UABU2Cmax=U2+U2RL=U2+U2R+U2LUCmax.UR=U.URL1U2R=1U2+1U2RL
=> Các phương án:
+ A, B, C – đúng
+ D – sai vì: 1U2R=1U2+1U2RL
Cho mạch điện RLC nối tiếp. Với cuộn dây thuần cảm có độ tự cảm L=12πHvà tụ điện có điện dung C thay đổi được. Điện áp giữa hai đầu đoạn mạch là u=U0cos(120πt)V. Điện dung C bằng bao nhiêu để điện áp hiệu dụng trên cuộn cảm L cực đại là:
+ Ta có, C biến thiên để ULmax <=> xảy ra hiện tượng cộng hưởng điện
Khi đó: →ZL=ZC
+ Cảm kháng: ZL=ωL=120π12π=60Ω
→ZC=60Ω=1ωC→C=1ωZC=1120π.60=44,2μF
Cho đoạn mạch điện xoay chiều RLC mắc nối tiếp có điện áp hai đầu đoạn mạch là u=120√6cos(100πt)V. Biết R=20√3Ω , ZL=20Ω và tụ điện có điện dụng C thay đổi được. Xác định C để UC cực đại và giá trị cực đại của UC bằng bao nhiêu?
Ta có: C thay đổi để UC max, khi đó:
+ Dung kháng:
ZC=R2+Z2LZL=(20√3)2+20220=80Ω→C=1ωZC=1100π.80=1,25.10−4πF
+ UCmax=U√R2+Z2LR=120√6√2√(20√3)2+20220√3=240(V)
Cho mạch điện xoay chiều như hình vẽ. Điện áp xoay chiều giữa hai đầu đoạn mạch có dạng u=240√2cos(100πt)V. Điều chỉnh C đến khi điện áp UNB đạt cực đại thì UAN=100V. Điện áp cực đại trên tụ điện đạt giá trị cực đại bằng:
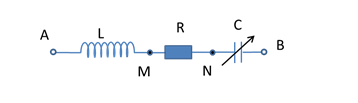
Khi C thay đổi để UCmax , khi đó, ta có: U⊥URL hay
U2Cmax=U2+U2RL=2402+1002→UCmax=260(V)
→U0Cmax=260√2V
Trong mạch điện xoay chiều gồm R,L,C mắc nối tiếp. Cho L,R,ω không đổi. Thay đổi C đến khi C=C0 thì cường độ dòng điện trong mạch đạt giá trị cực đại. Khi đó:
Ta có: C biến thiên để Imax <=> mạch xảy ra hiện tượng cộng hưởng điện
Khi đó:
↔ZC=ZL↔1ωC0=ωL→C0=1ω2L
Trong mạch điện xoay chiều gồm R,L,C mắc nối tiếp. Cho L,R,ω không đổi. Thay đổi C đến khi C=C0 thì điện áp hiệu dụng trên điện trở R đạt giá trị cực đại. Khi đó:
Ta có: Cbiến thiên để URmax <=> mạch xảy ra hiện tượng cộng hưởng điện
Khi đó:
↔ZC=ZL↔1ωC0=ωL→C0=1ω2L
Trong mạch điện xoay chiều gồm R,L,C mắc nối tiếp. Cho L,R,ω không đổi. Thay đổi C đến khi C=C0 thì điện áp hiệu dụng trên 2 đầu LC đạt giá trị nhỏ nhất. Khi đó:
Ta có: C biến thiên để ULCmin <=> mạch xảy ra hiện tượng cộng hưởng điện
Khi đó:
↔ZC=ZL↔1ωC0=ωL→C0=1ω2L
Trong mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Cho L,R,ω không đổi. Thay đổi C đến khi C=C0 thì công suất Pmax. Khi đó, Z tổng trở và công suất cực đại Pmax đó được xác định bởi biểu thức:
C thay đổi để Pmax , khi đó, mạch xảy ra cộng hưởng
ZL=ZC và {Zmin=RImax=URURmax=UPmax=I2R=U2R
Trong mạch điện xoay chiều gồm R,L,C mắc nối tiếp. Cho L,R,ω không đổi. Thay đổi C đến khi C=C0 thì điện áp URmax. Khi đó, cường độ dòng điện hiệu dụng trong mạch đó được xác định bởi biểu thức:
C thay đổi để URmax , khi đó, mạch xảy ra cộng hưởng
ZL=ZC và {Zmin=RImax=URURmax=UPmax=I2R=U2R
Trong mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Cho L,R,ωkhông đổi. Thay đổi C đến khi C=C0 thì điện áp hiệu dụng trên hai đầu cuộn cảm đạt cực đại. Khi đó, điện áp hiệu dụng trên tụ điện đó được xác định bởi biểu thức:
C thay đổi để ULmax, khi đó mạch xảy ra cộng hưởng điện
ZL=ZC và {Zmin=RImax=URURmax=UPmax=I2R=U2R
Ta có, điện áp hiệu dụng trên hai đầu tụ điện: UC=I.ZC=URZC=URZL (vì ZL=ZC)
Trong mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Cho L,R,ω không đổi. Thay đổi C đến khi C=C0 thì trong mạch xảy ra cộng hưởng. Phát biểu nào sau đây là đúng?
C thay đổi để mạch xảy ra cộng hưởng khi đó: ZL=ZC và {Zmin=RImax=URURmax=UPmax=I2R=U2R
A – sai vì: Zmin=R
B – sai vì: Imax=UR
C - đúng
D - sai vì khi đó u và i cùng pha với nhau (φu=φi)
Đoạn mạch xoay chiều RLC. Cuộn thuần cảm thuần, tụ điện có điện dung thay đổi được, điện trở thuần R=60Ω. Hiệu điện thế hai đầu mạch u=120cos(100πt)V. Thay đổi điện dung của tụ điện đến khi cường độ cực đại trong mạch có giá trị cực đại. Giá trị cực đại đó là:
Ta có cường độ dòng điện cực đại trong mạch có giá trị cực đại khi mạch xảy ra hiện tượng cộng hưởng điện
→I0max=U0R=12060=2(A)
Cho mạch điện gồm R, L, C mắc nối tiếp. Cho R=80Ω,L=12π(H), C thay đổi được. Đặt vào hai đầu mạch điện một điện áp xoay chiều u=160cos(100πt+π3)V. Khi C=C0 thì điện áp hiệu dụng giữa hai đầu điện trở đạt giá trị cực đại. Khi đó, biểu thức điện áp giữa hai đầu cuộn cảm là:
- Ta có: C biến thiên để URmax khi mạch xảy ra hiện tượng cộng hưởng điện: ZL=ZC
+ Cường độ dòng điện cực đại khi đó: I0=U0R=16080=2(A)
+ Mạch xảy cộng hưởng => u, i cùng pha →φi=φu=π3(rad)
- Cảm kháng: ZL=ωL=12π.100π=50Ω
- Hiệu điện thế cực đại giữa hai đầu cuộn cảm: U0L=I0ZL=2.50=100(V)
- Mặt khác, ta có uL nhanh pha hơn i một góc π2(rad)
→φuL=φi+π2=π3+π2=5π6(rad)
=> Biểu thức điện áp giữa hai đầu cuộn cảm: uL=100cos(100πt+5π6)V
Đặt điện áp u=U√2cos(ωt)V vào hai đầu đoạn mạch nối tiếp gồm R=40Ω,cuộn cảm có độ tự cảm L và tụ điện có điện dung C thay đổi được. Khi C=C1=50πμF thì cường độ dòng điện qua mạch cực đại. Khi C=C12 thì điện áp ở đầu tụ điện đạt cực đại. Tần số góc ω bằng?
Ta có:
+ Khi : cường độ dòng điện qua mạch cực đại
=> Khi đó mạch cộng hưởng: ZC1=ZL(1)
+ Khi C=C12→ZC=2ZC1: thì UCmax , khi đó ta có:
ZC=R2+Z2LZL=2ZC1 (2)
Từ (1) và (2): →R2+ZL2ZL=2ZL→R=ZL=ZC1=40Ω
Mặt khác: ZC1=1ωC1→ω=1ZC1.C1=140.50π.10−6=500π(rad/s)
Đoạn mạch gồm một cuộn dây có điện trở R và độ tự cảm L nối tiếp với một tụ điện biến đổi có điện dung thay đổi được . Điện áp xoay chiều ở hai đầu đoạn mạch là u=U√2cos(ωt)V. Khi C=C1 thì công suất mạch là P=200W và cường độ dòng điện qua mạch là i=I√2cos(ωt+π3)A. Khi C=C2 thì công suất cực đại. Công suất của mạch khi C=C2 là:
- Khi C=C1 :
+ Khi C=C1 ta có độ lệch pha của u so với i là: φ=0−π3=−π3
Mặt khác, ta có:
tanφ=ZL−ZC1R↔tan(−π3)=ZL−ZC1R
→ZC1−ZL=√3R (1)
+ Công suất của mạch khi đó: P1=U2Z21R=U2R2+(ZL−ZC1)2R (2)
Thay (1) vào (2), ta được: P1=U2R2+3R2R=U24R (3)
- KhiC=C2:
+ Khi C=C2 thì công suất cực đại => Mạch xảy ra cộng hưởng →ZL=ZC2
+ Công suất khi đó: P2=U2R (4)
Lấy (3)(4) ta được: P1P2=14→P2=4P1=4.200=800W
Một cuộn dây mắc nối tiếp với tụ điện có điện dung thay đổi được rồi mắc vào nguồn điện xoay chiều có biểu thức u=U0cos(ωt)V. Thay đổi điện dung của tụ điện để công suất toả nhiệt trên cuộn dây đạt cực đại, khi đó điện áp hiệu dụng giữa hai bản tụ là 2U0, điện áp hiệu dụng giữa hai đầu cuộn dây là:
Ta có, mạch gồm cuộn dây mắc nối tiếp với tụ, trên cuộn dây tỏa nhiệt => cuộn dây không thuần cảm (có điện trở trong r≠0 )
+ Công suất tỏa nhiệt trên cuộn dây: Pd=I2r=U2Z2r=U2r2+(ZL−ZC)2r
→Pdmax khi ZL=ZC
=> Tổng trở của mạch Z=r, cường độ dòng điện trong mạch I=Ur
+ Theo đầu bài, ta có:
UC=2U0
Mà
UC=I.ZC=UrZC=U0√2rZC=2U0
→ZC=2√2r=ZL (1)
+ Hiệu điện thế hiệu dụng trên hai đầu cuộn dây:
Ud=I.Zd=Ur√r2+Z2L (2)
Thế (1) vào (2) ta được: Ud=Ur√r2+(2√2r)2=3U=3U0√2
Một đoạn mạch RLC không phân nhánh (hình dưới) gồm điện trở R=80Ω cuộn cảm thuần có cảm kháng bằng điện trở và tụ điện có dung kháng thay đổi được. Mắc vào hai đầu đoạn mạch xoay chiều có điện áp hiệu dụng không đổi và tần số 50Hz. Điều chỉnh C để điện áp giữa hai đầu MB cực đại, giá trị của C là:
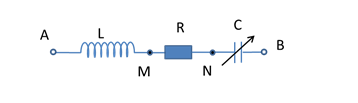
C thay đổi để URCmax , khi đó ta có:
ZC=ZL2
Theo đầu bài, ta có: ZL=R=80Ω→ZC=802=40Ω
Mặt khác: ZC=1ωC→C=1ωZC=12πfC=12π.50.40=14000πF
Cho đoạn mạch điện xoay chiều RLC có C thay đổi được. Khi C=C1 và C=C2 thì tổng trở của mạch không thay đổi. Khi đó ZC1+ZC2=?
Khi Z1=Z2
R2+(ZL−ZC1)2=R2+(ZL−ZC2)2→|ZL−ZC1|=|ZL−ZC2|
Với ZC2>ZC1→ZC1+ZC2=2ZL