Câu hỏi:
2 năm trước
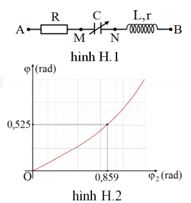
Đặt điện áp xoay chiều (có giá trị hiệu dụng và tần số không đổi) vào hai đầu đoạn mạch như hình H.1 thì cảm kháng của cuộn dây \({Z_L} = 2r\). Gọi \(\varphi \) và \({\varphi _2}\) tương ứng là độ lệch pha giữa điện áp \({u_{AB}}\) và \({u_{MB}}\) so với cường độ dòng điện trong mạch. Đồ thị biểu diễn sự phụ thuộc của \(\varphi \) vào \({\varphi _2}\) khi điện dung \(C\) thay đổi như hình H.2. Khi \(C = {C_0}\) thì điện áp \({u_{AN}}\) lệch pha \({90^0}\) so với \({u_{MB}}\). Khi đó, hệ số công suất của đoạn mạch \(MB\) là
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có: \(\left\{ \begin{array}{l}\tan \varphi = \frac{{{Z_{LC}}}}{{R + r}} = \tan 0,525\\\tan {\varphi _2} = \frac{{{Z_{LC}}}}{r} = \tan 0,859\end{array} \right. \Rightarrow \frac{{R + r}}{r} = 2 \Rightarrow R = r\)
Lấy \(R = 1 = r \Rightarrow {Z_L} = 2\)
Theo bài ta có: \({u_{AN}} \bot {u_{MB}} \Rightarrow \frac{{{Z_{{C_0}}}}}{R}.\frac{{{Z_L} - {Z_{{C_0}}}}}{r} = 1 \Rightarrow {Z_{{C_0}}} = 1.\)
Hệ số công suất của đoạn mạch \(MB\) là:
\(\cos {\varphi _{MB}} = \frac{r}{{\sqrt {{r^2} + {{\left( {{Z_L} - {Z_{{C_0}}}} \right)}^2}} }} = \frac{1}{{\sqrt 2 }} = 0,71.\)
Hướng dẫn giải:
Sử dụng công thức tính \(\tan \varphi \) cho đoạn mạch \(AB\) và \(MB.\)
Dựa vào \({u_{AN}} \bot {u_{MB}} \Rightarrow \frac{{{Z_{{C_0}}}}}{R}.\frac{{{Z_L} - {Z_{{C_0}}}}}{r} = 1\) → \({Z_{{C_0}}}\) → \(\cos {\varphi _{MB}}.\)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
