Bài tập mạch xoay chiều RLC - có C thay đổi

A – sai vì: \({Z_C} = \dfrac{{{Z_L}}}{2}\) thì \({U_{R{C_{max}}}}\)

B – sai vì: khi \({Z_C} = 2{Z_L}\) thì \({U_{RL}}\) không phụ thuộc vào R

C - đúng

D - sai vì: Khi \({Z_C} = {\rm{ }}2{Z_L}\) thì \({U_{RL}} = {U_{AB}}\) và không phụ thuộc vào R

Ta có điện áp ở hai đầu đoạn AM sớm pha hơn cường độ dòng điện một góc \({30^0} = \dfrac{\pi }{6}\left( {rad} \right)\)

Điện áp ở hai đầu MB trễ pha hơn cường độ dòng điện một góc \(\dfrac{\pi }{2}\left( {rad} \right)\) (do MB chỉ có tụ điện)

=> Độ lệch pha của AM so với MB là: \(\Delta \varphi  = \dfrac{\pi }{6} + \dfrac{\pi }{2} = \dfrac{{2\pi }}{3}\left( {rad} \right)\) 

Ta có, hiệu điện thế hiệu dụng của toàn mạch:

\(\begin{array}{l}{U^2} = U_{AM}^2 + U_{MB}^2 + 2{U_{AM}}{U_{MB}}{\rm{cos}}\Delta \varphi \\ = U_{AM}^2 + U_{MB}^2 + 2{U_{AM}}{U_{MB}}{\rm{cos}}\left( {\dfrac{{2\pi }}{3}} \right)\end{array}\)

Đặt: \({U_{AM}} = {\rm{ }}x\)  và \({U_{MB}} = {\rm{ }}y\)

\(\begin{array}{l} \to {U^2} = {x^2} + {y^2} + 2xyc{\rm{os}}\dfrac{{2\pi }}{3}\\ \leftrightarrow {U^2} = {x^2} + {y^2} - xy = {\left( {x + y} \right)^2} - 3{\rm{x}}y\end{array}\)

Theo BĐT cosi, ta có: \(xy \le \dfrac{{{{\left( {x + y} \right)}^2}}}{4}\)

\(\begin{array}{l} \to {U^2} = {\left( {x + y} \right)^2} - 3{\rm{x}}y \ge {\left( {x + y} \right)^2} - \dfrac{{3{{\left( {x + y} \right)}^2}}}{4} = \dfrac{1}{4}{\left( {x + y} \right)^2}\\ \to {\left( {x + y} \right)^2} \le 4{U^2} \to x + y \le 2U\end{array}\)

=> \(\left( {{U_{AM}} + {\rm{ }}{U_{MB}}} \right){\rm{ }}max{\rm{ }} = {\rm{ }}2U\)

Dấu bằng xảy ra <=> \(x = y = U = \dfrac{{160}}{{\sqrt 2 }} = 80\sqrt 2 V\)

+ Cảm kháng: \({Z_L} = \omega L = 100.0,7 = 70\Omega \)

+ Khi\(C = {C_0}\)  thì u cùng pha với i mạch => mạch xảy ra hiện tượng cộng hưởng điện

\( \to {Z_L} = {Z_{{C_0}}} = 70\Omega \)

Cường độ dòng điện cực đại khi đó: \({I_0} = \dfrac{{{U_0}}}{Z} = \dfrac{{{U_0}}}{r} = \dfrac{{140}}{{70}} = 2A\)

=> Hiệu điện thế cực đại trên tụ: \({U_0} = {I_0}{Z_C} = 2.70 = 140V\)

Vì u cùng pha với i \( \to {\varphi _u} = {\varphi _i} =  - \dfrac{\pi }{4}\left( {rad} \right)\)

+ Ta có \({u_C}\) trễ pha hơn \(i\) một góc \(\dfrac{\pi }{2}\)

\( \to {\varphi _{{u_C}}} = {\varphi _i} - \dfrac{\pi }{2} =  - \dfrac{\pi }{4} - \dfrac{\pi }{2} =  - \dfrac{{3\pi }}{4}\left( {rad} \right)\)

=> Biểu thức điện áp trên tụ: \({u_C} = 140cos\left( {100t - \dfrac{{3\pi }}{4}} \right)V\)

+ Ta có: \({U_{C\max }} = \dfrac{{U\sqrt {{R^2} + Z_L^2} }}{R} \Rightarrow 160 = \dfrac{{80\sqrt {{{20}^2}.3 + Z_L^2} }}{{20\sqrt 3 }} \Rightarrow {Z_L} = 60\Omega .\)

+ U_C = U_Cmax khi   \({Z_{C0}} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}} = \dfrac{{{{20}^2}.3 + {{60}^2}}}{{60}} = 80\Omega .\) 

+ Độ lệch pha của u so với i:

\(\begin{array}{l}\tan \varphi  = \dfrac{{{Z_L} - {Z_{{C_0}}}}}{R} =  - \dfrac{1}{{\sqrt 3 }}\\ \Rightarrow \varphi  =  - \dfrac{\pi }{6}\end{array}\)

\(\begin{array}{l} \Rightarrow {\varphi _u} - {\varphi _i} =  - \dfrac{\pi }{6}\\ \Rightarrow {\varphi _i} = {\varphi _u} + \dfrac{\pi }{6} =  - \dfrac{\pi }{4} + \dfrac{\pi }{6} =  - \dfrac{\pi }{{12}}\end{array}\)

+ Mặt khác: \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_{C0}})}^2}}  = 40\Omega .\) 

Ta suy ra, cường độ dòng điện cực đại: \({I_0} = \dfrac{{{U_0}}}{Z} = \dfrac{{80\sqrt 2 }}{{40}} = 2\sqrt 2 \left( A \right)\)

Suy ra, biểu thức cường độ dòng điện trong mạch: \(i = 2\sqrt 2 \cos (100\pi t - \dfrac{\pi }{{12}})(A).\)

C thay đổi để U_C max, khi đó: \({Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}\)

Thay đổi C để U_C cực đại, giá trị cực đại của U_C  khi đó là: \({U_{Cm{\rm{ax}}}} = \dfrac{{U_R^2 + U_L^2}}{{{U_L}}} = \dfrac{{U\sqrt {{R^2} + Z_L^2} }}{R}\)

Ta có C thay đổi để U_C max, khi đó: \({U_{Cm{\rm{ax}}}} = \dfrac{{U_R^2 + U_L^2}}{{{U_L}}} = \dfrac{{U\sqrt {{R^2} + Z_L^2} }}{R}\)

\(\left\{ \begin{array}{l}{U_{RL}} \bot {U_{AB}}\\U_{C\max }^2 = {U^2} + U_{RL}^2 = {U^2} + U_R^2 + U_L^2\\U_{C\max }^{}.{U_R} = U.{U_{RL}}\\\dfrac{1}{{U_R^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RL}^2}}\end{array} \right.\)

Ta có: C biến thiên để U­_L max <=> xảy ra hiện tượng cộng hưởng điện

\( \to {Z_L} = {Z_C}\)

Ta có: Cảm kháng: \({Z_L} = \omega L = 100\pi \dfrac{1}{\pi } = 100\Omega \)

\( \to {Z_C} = 100\Omega  = \dfrac{1}{{\omega C}} \to C = \dfrac{1}{{\omega {Z_C}}} = \dfrac{1}{{100\pi .100}} = \dfrac{{{{10}^{ - 4}}}}{\pi }F = \dfrac{{100}}{\pi }\mu F\)

Ta có: C thay đổi để U_C max, khi đó:

+ Dung kháng: s

\(\begin{array}{l}{Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}} = \dfrac{{{{(10\sqrt 3 )}^2} + {{30}^2}}}{{30}} = 40\Omega \\ \to C = \dfrac{1}{{\omega {Z_C}}} = \dfrac{1}{{100\pi .40}} = \dfrac{{{{2,5.10}^{ - 4}}}}{\pi }F\end{array}\)

+ \({U_{Cm{\rm{ax}}}} = \dfrac{{U\sqrt {{R^2} + Z_L^2} }}{R} = \dfrac{{120\sqrt {{{(10\sqrt 3 )}^2} + {{30}^2}} }}{{10\sqrt 3 }} = 240(V)\)

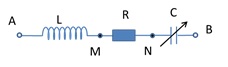
khi C thay đổi để U_C max, khi đó:

\(\begin{array}{l}U_{C\max }^2 = {U^2} + U_{RL}^2 = {160^2} + {120^2}\\ \to {U_{{C_{max}}}} = 200(V)\end{array}\)

Ta có: C biến thiên để U_L max <=> mạch xảy ra hiện tượng cộng hưởng điện

\(\begin{array}{l} \leftrightarrow {Z_C} = {Z_L} \leftrightarrow \frac{1}{{\omega {C_0}}} = \omega L\\ \to {C_0} = \frac{1}{{{\omega ^2}L}}\end{array}\)

C thay đổi để P_max, khi đó: \({Z_L} = {Z_C}\) và \({P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\)

C thay đổi để U_Rmax, khi đó: \({Z_L} = {Z_C}\) và \(U = {U_{Rm{\rm{ax}}}}\)

C thay đổi để U_Lmax, khi đó: \({Z_L} = {Z_C}\)

\(\begin{array}{l}Z = R \to I = \dfrac{U}{R}\\ \to {U_{Lm{\rm{ax}}}} = I{Z_L} = \dfrac{U}{R}{Z_L}\end{array}\)

C thay đổi để mạch xảy ra cộng hưởng khi đó: \({Z_L} = {Z_C}\)

A, B, C - đúng

D- sai vì khi đó u và i cùng pha với nhau

Ta có cường độ dòng điện hiệu dụng có giá trị cực đại khi mạch xảy ra hiện tượng cộng hưởng điện

\( \to {I_{{\rm{max}}}} = \dfrac{U}{R} = \dfrac{{\dfrac{{200}}{{\sqrt 2 }}}}{{100}} = \sqrt 2 (A)\)

Ta có:  U_Rmax khi mạch xảy ra hiện tượng cộng hưởng điện: \({Z_L} = {Z_C}\)

Cường độ dòng điện khi đó: \({I_0} = \frac{{{U_0}}}{R} = \frac{{120}}{{60}} = 2(A)\)

+ Cảm kháng: \({Z_L} = \omega L = \frac{{0,3}}{\pi }.100\pi  = 30\Omega \)

Hiệu điện thế cực đại trên giữa hai đầu cuộn cảm: \({U_{0L}} = {I_0}{Z_L} = 2.30 = 60(V)\)

ta có, mạch xảy cộng hưởng => u, i cùng pha

Mặt khác, ta có u_L nhanh pha hơn i một góc \(\frac{\pi }{2}(ra{\rm{d}})\)

=> Biểu thức điện áp giữa hai đầu cuộn cảm: \(u = 60c{\rm{os(100}}\pi {\rm{t + }}\pi )V\)

Ta có:

+ Khi C = C₁: cường độ dòng điện qua mạch cực đại

=> Khi đó mạch cộng hưởng: \({Z_{{C_1}}} = {Z_L}\) (1)

+ Khi \(C = \frac{{{C_1}}}{2} \to {Z_C} = 2{Z_{{C_1}}}\): thì U_C max, khi đó ta có:

\({Z_C} = \frac{{{R^2} + Z_L^2}}{{{Z_L}}} = 2{Z_{{C_1}}}\) (2)

Từ (1) và (2): \( \to \frac{{{R^2} + {Z_L}^2}}{{{Z_L}}} = 2{Z_L} \to R = {Z_L} = {Z_{{C_1}}} = 100\Omega \)

Mặt khác:  \({Z_{{C_1}}} = \frac{1}{{\omega {C_1}}} \to \omega  = \frac{1}{{{Z_{{C_1}}}.{C_1}}} = \frac{1}{{100.\frac{{100}}{\pi }{{.10}^{ - 6}}}} = 100\pi (ra{\rm{d}}/s)\)

C thay đổi để P_max => Mạch cộng hưởng \({Z_L} = {Z_C}\)

Ta có: \({Z_L} = \omega L = 100\pi .\dfrac{2}{\pi } = 200\Omega \)

\( \to {Z_C} = 200\Omega  = \dfrac{1}{{\omega C}} \to C = \dfrac{1}{{\omega {Z_C}}} = \dfrac{1}{{100\pi .200}} = \dfrac{{50}}{\pi }\mu F\)

Cường độ dòng điện: \(I = \dfrac{U}{Z} = \dfrac{U}{{R + r}} = \dfrac{{200}}{{80 + 20}} = 2(A)\)

Công suất tiêu thụ trên mạch: \(P = {I^2}(R + r) = {2^2}(80 + 20) = 400{\rm{W}}\)

Điện dung C thay đổiU_RC cực đại khi đó: 

\({Z_C} = \frac{{{Z_L} + \sqrt {4{R^2} + Z_L^2} }}{2}\)