Trong đêm hoan ca văn nghệ kỉ niệm 45 năm ngày thành lập trường THPT Thanh Oai B. Mở màn đêm diễn là lớp 12A2, coi mọi học sinh đều hát với cùng cường độ âm và cùng tần số. Khi một học sinh hát thì mức cường độ âm là 68dB. Khi cả đội cùng hát thì đo được mức cường độ âm là 80dB. Số học sinh lớp 12A2 có trong tốp ca này là:
Ta có
{L1=10log(P4πr2)Ln=10log(nP4πr2)=>Ln−L1=10logn
=>n=10Ln−L110≈16 người
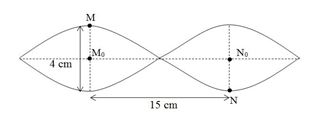
Một sóng cơ học truyền trên sợi dây dài nằm ngang với bước sóng λ=20cm và biên độ dao động A=4cm không đổi khi truyền đi. Gọi MN là hai điểm trên dây cách nhau một đoạn 25cm theo phương ngang. Tính khoảng cách lớn nhất và nhỏ nhất giữa hai điểm MN ?
Độ lệch pha của M và N là: Δφ=2πdλ=π3
Lệch pha về thời gian: Δt=π3.T2π=T6
Từ giản đồ Fresnel, ta có: A2=a2⇒A=a
Khoảng thời gian ngắn nhất phần tử M tới biên dương là: khoảng thời gian M đi từ a2 đến a:
Δφ=2π−π3=5π3⇒Δt=5T6.
Trên một sợi dây dài 30cm, hai đầu cố định đang có sóng dừng. Trên dây có tất cả 2 điểm M,N luôn dao động với biên độ cực đại là 2cm. Chọn phương án chính xác nhất.
Trên dây có 2 điểm luôn dao động với biên độ cực đại => trên dây chỉ có 2 bụng sóng => λ=30cm
M và N dao động ngược pha.
MNmin khi M và N cùng ở vị trí cân bằng M0, N0→M0N0=λ2=15cm
MNmax khi M và N cùng ở bụng sóng →MNmax=√152+42=15,5cm
⇒15≤MN≤15,6
⇒ Phương án A đúng nhất
Trên một sợi dây AB dài 1,2m đang có sóng dừng với 3 bụng sóng, biên độ bụng sóng a=4√2cm . Tốc độ truyền sóng trên dây v=80cm/s. Biết hai đầu A,B là các nút sóng. Ở thời điểm phần tử tại điểm M trên dây cách A 30cm có li độ 2cm thì phần tử tại điểm N trên dây cách B 50cm có tốc độ là:
Điều kiện sóng dừng với hai đầu dây cố định :
ℓ=kλ2⇒λ=80cm(k=3)
⇒f=vλ=1Hz⇒ω=2πrad/s
Biên độ của một điểm cách nút một khoảng d là :
A=2a|sin2πdλ|→{AM=4cmAN=4cm
Do AM=AN
Lại có: A2=x2+v2ω2
=> Tốc độ |vM|=|vN|=ω√A2M−x2M=2π√42−22=4π√3cm/s
Trong thí nghiệm giao thoa sóng nước, hai nguồn S1 và S2 cách nhau 16cm, dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 80Hz. Tốc độ truyền sóng trên mặt nước là 40cm/s. Ở mặt nước, gọi Δ là đường trung trực của đoạn S1S2 . Trên Δ điểm M cách S1 10cm, điểm N dao động cùng pha với M và gần M nhất sẽ cách M một đoạn:
Ta có :
M chậm pha so với nguồn : ΔφM=2π.AMλ=40π
Điểm N cùng pha với M :
⇒[ΔφN=42πΔφN=38π
Với :
∗ΔφN=42π⇒2πANλ=42π⇔AN=10,5cm⇒OM=6,8cm⇒MN=NO−MO=0,8=8mm
∗ΔφN=38π⇒2πANλ=38π⇔AN=9,5cm⇒OM=5,12cm⇒MN=NO−MO=0,876cm(loai)
Vậy N cách M gần nhất một đoạn 8mm
Một sợi dây đang có sóng dừng ổn định. Sóng truyền trên dây có tần số 10Hz và bước sóng 6cm . Trên dây, hai phần tử M và N có vị trí cân bằng cách nhau 8cm, M thuộc một bụng sóng dao động điều hòa với biên độ 6mm. Lấy π2=10. Tại thời điểm t, phần tử M đang chuyển động với tốc độ 6π(cm/s) thì phần tử N chuyển động với gia tốc có độ lớn là:
Bước sóng 6 cm nên chiều dài 1 bó sóng là 3 cm. M thuộc bụng sóng và MN = 8 cm nên ta suy được vị trí của N như hình vẽ. Từ vị trí của N ta suy ra N dao động ngược pha với M.
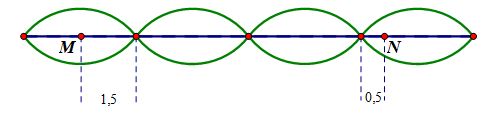
N cách điểm nút gần nhất 1 khoảng x = 0,5 cm nên biên độ của N: AN=AM|cos(2πxλ−π2)|=AM2=3(mm).
Vận tốc cực đại của M: vmax=2AMπf=12π(cm/s).
Thời điểm t, vM = vmax/2 suy ra xM=±AM√32. Vì N ngược pha M nên có xN=∓AN√32.
Độ lớn gia tốc của N tại t: |aN|=ω2|xN|=4π2f2.√32AN=6√3(m/s2).
Cho 4 điểm O,M,N và P nằm trong một môi trường truyền âm. Trong đó, M và N nằm trên nửa đường thẳng xuất phát từ O, tam giác MNP là tam giác đều. Tại O, đặt một nguồn âm điểm có công suất không đổi, phát âm đẳng hướng ra môi trường. Coi môi trường không hấp thụ âm. Biết mức cường độ âm tại M và N lần lượt là 50dB và 40dB. Mức cường độ âm tại P là:
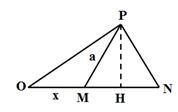
LM=50dB→IM=105I0=P4πx2LN=40dB→IM=104I0=P4π(x+a)2
⇒IMIN=10=(x+a)2x2⇒x=a√10−1
OP2=PH2+OH2=(a√32)2+(x+a2)2=a2.(34+(12+1√10−1)2)
IPIM=OM2OP2⇒IP≈12758,8.I0⇒LP=41,1dB
Tại mặt nước có hai nguồn sóng A,B giống hệt nhau cách nhau 8cm, gọi M,N là hai điểm trên mặt nước sao cho MN=4cm và tạo với ABmột hình thang cân (MN//AB), biết M,N dao động với biên độ cực đại. Bước sóng trên mặt nước là 1cm. Để trên đoạn MN có đúng 5 điểm dao động cực đại thì diện tích của hình thang phải là:
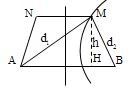
Để trên đoạn MN có 5 cực đại thì M phải thuộc cực đại bậc 2 nên k=2
M là cực đại thì d1−d2=kλ=2.1=2cm(1)
Xét tam giác AHMcó:
d21=AM2=AH2+HM2=(AO+OH)2+h2=(AB2+OH)2+h2=62+h2(2)
Tương tự xét tam giác BMH có:
d22=BM2=BH2+HM2=(OB−OH)2+h2=(AB2−OH)2+h2=22+h2(3)
Lấy (2) trừ (3) vế theo vế ta có: d21−d22=32(4) từ (1) thay vào (4) suy ra:
(d1−d2)(d1+d2)=32⇒d1+d2=32d1−d2=322=16cm
Vậy ta có hệ: {d1−d2=2d1+d2=16⇒{d1=9cmd2=7cm Thay vào (2) suy ra: h=3√5cm
Vậy diện tích lớn nhất của hình thang: S=12.h(AB+MN)=18√5cm2.
Ở mặt chất lỏng có 2 nguồn kết hợp đặt tại A và B dao động điều hòa, cùng pha theo phương thẳng đứng. Ax là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với AB. Trên Ax có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó M là điểm xa A nhất, N là điểm kế tiếp với M, P là điểm kế tiếp với N và Q là điểm gần A nhất. Biết MN=22,25cm, NP=8,75cm. Độ dài đoạn QA gần nhất với giá trị nào sau đây?
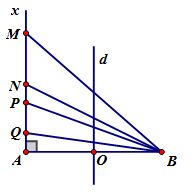
+ Ta thấy trên nửa đường thẳng kẻ từ A vuông góc với AB có 4 điểm theo thứ tự M,N,P,Q dao động với biên độ cực đại
=> Nên AB có 9 điểm dao động với biên độ cực đại với: −4≤k≤4(d2−d1=kλ)
Cực đại M,N,P,Q ứng với k=1,2,3,4
+ Đặt AB=a
Tại C trên Ax là điểm dao động với biên độ cực đại:
CB−CA=kλ(∗)
CB2−CA2=a2→(CB−CA)(CB+CA)=a2→CB+CA=a2kλ(∗∗)
Từ (∗) và (∗∗) ta suy ra: CA=a22kλ−kλ2
- Tại M ứng với k=1: MA=a22λ−λ2(1)
- Tại N ứng với k=2: NA=a22.2λ−2λ2=a24λ−λ(2)
- Tại P ứng với k=3: PA=a22.3λ−3λ2=a26λ−3λ2(3)
- Tại Q ứng với k=4: QA=a22.4λ−4λ2=a28λ−2λ(4)
Lấy (1)−(2) ta được: MN=MA−NA=a24λ+λ2=22,25cm(5)
Lấy (2)−(3) ta được: NP=NA−PA=a212λ+λ2=8,75cm(6)
Lấy 3.(6)−(5) ta được:
3(a212λ+λ2)−(a24+λ2)=3.8,75−22,25→λ=4cm
Lấy (5)−(6) ta được: a26λ=22,25−8,75=13,5cm→a2λ=81cm
Thay {λ=4cma2λ=81cm vào (4) ta được: QA=a28λ−2λ=818−2.4=2,125cm
Một sóng dừng trên dây có dạng u=2sin(2πxλ)cos(2πt−π2)mm. Trong đó u là li độ tại thời điểm t của phần tử P trên dây, x tính bằng cm là khoảng cách từ nút O của dây đến điểm P. Điểm trên dây dao động với biên độ bằng √2mm cách bụng sóng gần nhất đoạn 2cm. Vận tốc dao động của điểm trên dây cách nút 4cm ở thời điểm t=1s là:
Phương trình sóng dừng trên dây là:
u=2sin(2πxλ)cos(2πt−π2) (mm)
Tại điểm thứ nhất: A=2sin(2πxλ)=√2⇒2πxλ=(2k+14)π⇒x=(k+18)λ
Khoảng cách từ điểm đó tới bụng sóng gần nhất là: λ8=2⇒λ=16(cm)
Điểm cần tìm cách nút 4cm=λ4
→ Điểm đó là bụng: A=2(cm)
Vậy li độ u của điểm đó là: 0(cm) theo chiều dương →v=ωA=4πmm/s
Thực hiện giao thoa sóng cơ với hai nguồn hoàn toàn giống nhau. Hai nguồn đặt tại hai điểm A và B, với B cố định còn A thay đổi được. Ban đầu khi thực hiện giao thoa thì thấy với M cách A một khoảng dA=28cm, cách B một khoảng dB=32cm là một điểm cực đại giao thoa. Sau đó người ta dịch chuyển điểm A ra xa điểm B dọc theo đường thẳng nối hai điểm A và B thì thấy có 2 lần điểm M là cực đại giao thoa, lần thứ 2 thì đường cực đại qua M là dạng đường thẳng và vị trí A lúc này cách vị trí ban đầu một khoảng x=12cm. Hãy xác định số điểm cực đại trong khoảng nối giữa A và B khi chưa dịch chuyển nguồn?
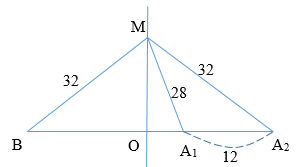
- Ban đầu: Δd1=k.λ→32−28=4=k.λ (1)
- Sau khi dịch chuyển A: Δd2=(k−2).λ (2)
+ Đường cực đại qua M là đường thẳng
→k −2 = 0→k =2
Thay vào (1), ta suy ra: λ=2cm
Từ hình ta có: cos^MA2A1=MA21−MA22−A1A22−2MA2.A1A2=282−322−122−2.32.12=12=OA2MA2
Ta suy ra: OA2=MA22=322=16=OB
→OM=√MB2−OB2=√322−162=16√3cm→OA1=√MA21−OM2=√282−(16√3)2=4cm→BA1=OB+OA1=16+4=20cm
Số cực đại trên khoảng BA1:
−BA1λ<k<BA1λ↔−202<k<202↔−10<k<10→k=0,±1,±2,...,±9
=> Số cực đại trên khoảng BA1 là 19 điểm
Một nguồn âm tại O xem như nguồn điểm cho mức cường độ âm tại A là LA=30dB, mức cường độ âm tại B là LB=40dB. Biết OA và OB vuông góc với nhau. Bỏ qua sự hấp thụ âm của môi trường. Nếu đặt tại O thêm 9 nguồn âm giống như nguồn âm trên thì mức cường độ âm tại trung điểm của đoạn AB gần nhất với giá trị nào sau đây?
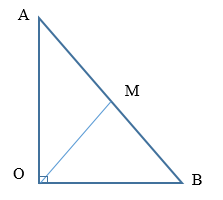
Ta có:
LB−LA=10logr2Ar2B↔40−30=10logr2Ar2B→r2Ar2B=101→rA=√10rB
Đặt rB=OB=a→OA=rA=√10a
→AB=√OB2+OA2=√11a
Vì ΔABO vuông tại O
Đường trung tuyến: OM=12AB=√11a2
LM1 - mức cường độ âm khi tại O có 1 nguồn âm
LM2 - mức cường độ âm khi tại O có 10 nguồn âm
Ta có:
LB−LM1=10logOM2OB2=10log(√11a2)2a2=4,39dB→LM1=LB−4,39=40−4,39=35,6dB
Mặt khác, ta có:
LM1=10logIM1I0↔35,6=10logIM1I0→IM1=1035,610I0=3630,8I0
Lại có: I=P4πr2
Ta suy ra: IM1IM2=P1P2=P10P=110→IM2=10IM1=36308I0
→LM2=10logIM2I0=10log36308I0I0=45,6dB
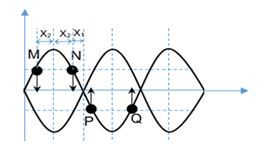
Sóng dừng trên một sợi dây với biên độ điểm bụng là 4cm. Hình bên biểu diễn hình dạng sợi dây tại hai thời điểm t1 và t2. Ở thời điểm t1 điểm bụng M đang chuyển động với tốc độ bằng tốc độ chuyển động của điểm N ở thời điểm t2 . Tọa độ của điểm N tại thời điểm t2 là:
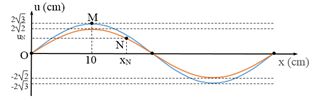
Ta có đường màu xanh là thời điểm t1
Để ý khoảng cách từ O đến M chính là khoảng cách từ nút sóng tới bụng sóng gần nhất: λ4=10cm→λ=40cm
+ Theo đầu bài, ta có:
|vM1|=|vN2|⇒ω√A2M−u2M1=ω√A2N−u2N2⇒√42−(2√3)2=√A2N−u2N2(1)
+ Lại có: AN=4|sin2πxNλ| (2)
Từ (1) và (2) kết hợp với đáp án ta suy ra phương án C đúng.
Một nguồn O phát sóng cơ dao động theo phương trình u=2cos(20πt+π3)mm , t tính bằng s. Sóng truyền theo đường thẳng Ox với tốc độ 1m/s. Trên một phương truyền sóng, trong khoảng từ O đến M (cách O 42,5cm) có bao nhiêu điểm mà các phần tử ở đó và các phần tử ở nguồn dao động lệch pha nhau π6 ?
Bước sóng λ=vf=120π2π=0,1m=10cm
Độ lệch pha giữa một điểm nằm trên phương truyền sóng và phần tử ở nguồn O là Δφ=2πdλ
Theo bài: Δφ=π6=>2πΔdλ=π6=>Δd=λ12
Có 42,5=4λ+λ4
Trên phương truyền sóng, hai điểm cách nhau λ thì cùng pha
=> từ O đến M có 4 điểm O1,O2,O3,O4 cùng pha với O
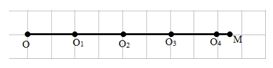
Những điểm lệch pha với O1,O2,O3,O4 góc π6 thì cũng lệch pha với O góc π6. Trong khoảng O đến O1 có 2 điểm lệch pha với O và O1 góc π6
=> Từ O đến O4 có 8 điểm lệch pha với O góc π6
Có điểm gần nhất lệch pha π6 so với O cách O một đoạn bằng λ12
=> Trong khoảng từ O4 đến M có 1 điểm lệch pha với O góc π6
=> Từ 0 đến M có 9 điểm lệch pha với O góc π6
Từ điểm A bắt đầu thả rơi tự do một nguồn phát âm có công suất không đổi, khi chạm đất tại B nguồn âm đứng yên luôn. Tại C ở khoảng giữa A và B (nhưng không thuộc AB), có một máy M đo mức cường độ âm, C cách AB 12m. Biết khoảng thời gian từ khi thả nguồn đến khi máy M thu được âm có mức cường độ âm cực đại, lớn hơn 1,528s so với khoảng thời gian từ đó đến khi máy M thu được âm có mức cường độ âm không đổi; đồng thời hiệu hai khoảng cách tương ứng này là 11m. Bỏ qua sức cản không khí, lấy g=10m/s2. Hiệu giữa mức cường độ âm cuối cùng và đầu tiên xấp xỉ:
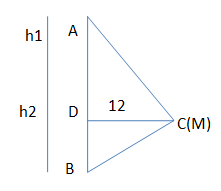
M thu được âm có mức cường độ âm cực đại khi nguồn âm tại D với AD⊥CD
M thu được âm không đổi khi nguồn âm đứng yên tại B
Thời gian rơi và quãng đường rơi được từ A→D lần lượt là t1 và h1
Thời gian rơi và quãng đường đi được từ D→B lần lượt là t2 và h2
Theo đề: t1−t2=1,528s(t1>1,528s) và h1−h2=11m
Áp dụng công thức rơi tự do : s1=h1=12gt21và s2=h1+h2=12g(t1+t2)2=12g(2t1−1,528)2
Suy ra 2s1−s2=h1−h2=gt21−12g(2t1−1,528)2
↔10t21−30,56 t1+ 22,67392 = 0→[t1=1,787599692t2=1,268400308.
Nhận nghiệm t1=1,787599692s→h1=16m và h2=5m
Suy ra :
LB−LA=10logIBIA=10logCA2CB2=10logAD2+DC2BD2+DC2=10log162+12252+122=3,74dB

