Một sóng dừng trên dây có dạng \(u = 2\sin \left( {\frac{{2\pi x}}{\lambda }} \right){\rm{cos}}\left( {2\pi t - \frac{\pi }{2}} \right)mm\). Trong đó \(u\) là li độ tại thời điểm t của phần tử P trên dây, x tính bằng cm là khoảng cách từ nút O của dây đến điểm P. Điểm trên dây dao động với biên độ bằng \(\sqrt 2 mm\) cách bụng sóng gần nhất đoạn \(2{\rm{ }}cm\). Vận tốc dao động của điểm trên dây cách nút \(4{\rm{ }}cm\) ở thời điểm \(t{\rm{ }} = {\rm{ }}1{\rm{ }}s\) là:
Trả lời bởi giáo viên
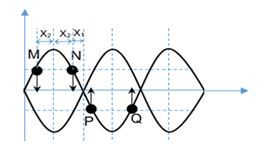
Phương trình sóng dừng trên dây là:
\(u = 2\sin \left( {\frac{{2\pi x}}{\lambda }} \right)\cos \left( {2\pi t - \frac{\pi }{2}} \right)\) (mm)
Tại điểm thứ nhất: \(A = 2\sin \left( {\frac{{2\pi x}}{\lambda }} \right) = \sqrt 2 \Rightarrow \frac{{2\pi x}}{\lambda } = \left( {2k + \frac{1}{4}} \right)\pi \Rightarrow x = \left( {k + \frac{1}{8}} \right)\lambda \)
Khoảng cách từ điểm đó tới bụng sóng gần nhất là: \(\frac{\lambda }{8} = 2 \Rightarrow \lambda = 16\left( {cm} \right)\)
Điểm cần tìm cách nút \(4{\rm{ }}cm = \frac{\lambda }{4}\)
→ Điểm đó là bụng: \(A{\rm{ }} = {\rm{ }}2{\rm{ }}\left( {cm} \right)\)
Vậy li độ u của điểm đó là: \(0{\rm{ }}\left( {cm} \right)\) theo chiều dương \( \to v{\rm{ }} = {\rm{ }}\omega A{\rm{ }} = {\rm{ }}4\pi {\rm{ }}mm/s\)
Hướng dẫn giải:
+ Từ phương trình sóng => xác định biên độ của mỗi điểm
+ Vẽ trên phương truyền sóng

