Cho \(4\) điểm \(O,{\rm{ }}M,{\rm{ }}N\) và \(P\) nằm trong một môi trường truyền âm. Trong đó, \(M\) và \(N\) nằm trên nửa đường thẳng xuất phát từ \(O\), tam giác \(MNP\) là tam giác đều. Tại \(O\), đặt một nguồn âm điểm có công suất không đổi, phát âm đẳng hướng ra môi trường. Coi môi trường không hấp thụ âm. Biết mức cường độ âm tại \(M\) và \(N\) lần lượt là \(50{\rm{ }}dB\) và \(40{\rm{ }}dB\). Mức cường độ âm tại P là:
Trả lời bởi giáo viên
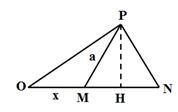
\(\begin{array}{l}{L_M} = 50{\rm{d}}B \to {I_M} = {10^5}{I_0} = \frac{P}{{4\pi {x^2}}}\\{L_N} = 40{\rm{d}}B \to {I_M} = {10^4}{I_0} = \frac{P}{{4\pi {{(x + a)}^2}}}\end{array}\)
\( \Rightarrow \frac{{{I_M}}}{{{I_N}}} = 10 = \frac{{{{(x + a)}^2}}}{{{x^2}}} \Rightarrow x = \frac{a}{{\sqrt {10} - 1}}\)
\(O{P^2} = P{H^2} + O{H^2} = {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} + {(x + \frac{a}{2})^2} = {a^2}.\left( {\frac{3}{4} + {{\left( {\frac{1}{2} + \frac{1}{{\sqrt {10} - 1}}} \right)}^2}} \right)\)
\(\frac{{{I_P}}}{{{I_M}}} = \frac{{O{M^2}}}{{O{P^2}}} \Rightarrow {I_P} \approx 12758,8.{I_0} \Rightarrow {L_P} = 41,1{\rm{d}}B\)
Hướng dẫn giải:
+ Sử dụng công thức tính cường độ âm và mức cường độ âm\(I = \frac{P}{{4\pi {r^2}}};L = 10.\log \frac{I}{{{I_0}}}\)
+ Sử dụng biểu thức tính hiệu mức cường độ âm : \({L_A} - {L_B} = 10\log \frac{{{I_A}}}{{{I_B}}} = 10\log \frac{{r_B^2}}{{r_A^2}}\)

