Trên một sợi dây dài \(30{\rm{ }}cm\), hai đầu cố định đang có sóng dừng. Trên dây có tất cả \(2\) điểm \(M,{\rm{ }}N\) luôn dao động với biên độ cực đại là \(2{\rm{ }}cm\). Chọn phương án chính xác nhất.
Trả lời bởi giáo viên
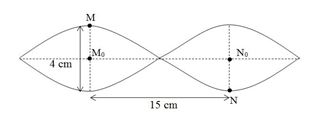
Trên dây có \(2\) điểm luôn dao động với biên độ cực đại => trên dây chỉ có 2 bụng sóng => \(\lambda = 30cm\)
M và N dao động ngược pha.
\(MN{\rm{ }}min\) khi M và N cùng ở vị trí cân bằng \({M_0},{\text{ }}{N_0} \to {M_0}{N_0} = \dfrac{\lambda }{2} = 15cm\)
\(MN{\rm{ }}max\) khi M và N cùng ở bụng sóng $ \to M{N_{max}} = \sqrt {{{15}^2} + {4^2}} = 15,5cm$
\( \Rightarrow 15 \le MN \le 15,6\)
\( \Rightarrow\) Phương án A đúng nhất
Hướng dẫn giải:
+ Sử dụng lí thuyết về sự truyền sóng và đường tròn lượng giác
+ Biểu thức tính khoảng cách giữa 2 điểm trên phương truyền sóng: \({d^2} = \Delta {x^2} + \Delta {u^2}\)

