Trong thí nghiệm giao thoa sóng nước, hai nguồn \({S_1}\) và \({S_2}\) cách nhau \(16cm\), dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số \(80Hz\). Tốc độ truyền sóng trên mặt nước là \(40cm/s\). Ở mặt nước, gọi \(\Delta \) là đường trung trực của đoạn \({S_1}{S_2}\) . Trên \(\Delta \) điểm \(M\) cách \({S_1}\) \(10cm\), điểm \(N\) dao động cùng pha với \(M\) và gần \(M\) nhất sẽ cách \(M\) một đoạn:
Trả lời bởi giáo viên
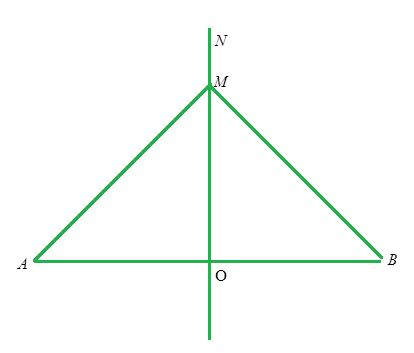
Ta có :
M chậm pha so với nguồn : \(\Delta {\varphi _M} = \dfrac{{2\pi .AM}}{\lambda } = 40\pi \)
Điểm N cùng pha với M :
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{\Delta {\varphi _N} = 42\pi }\\{\Delta {\varphi _N} = 38\pi }\end{array}} \right.\)
Với :
\(\begin{array}{l}*\Delta {\varphi _N} = 42\pi \\ \Rightarrow \dfrac{{2\pi AN}}{\lambda } = 42\pi \Leftrightarrow AN = 10,5cm\\ \Rightarrow OM = 6,8cm \Rightarrow MN = NO - MO = 0,8 = 8mm\end{array}\)
\(\begin{array}{l}*\Delta {\varphi _N} = 38\pi \\ \Rightarrow \dfrac{{2\pi AN}}{\lambda } = 38\pi \Leftrightarrow AN = 9,5cm\\ \Rightarrow OM = 5,12cm \Rightarrow MN = NO - MO = 0,876cm(loai)\end{array}\)
Vậy $N$ cách $M$ gần nhất một đoạn $8mm$
Hướng dẫn giải:
Sử dụng biểu thức tính độ lệch pha giữa hai điểm: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)

