Một sóng cơ học truyền trên sợi dây dài nằm ngang với bước sóng \(\lambda = {\rm{ }}20{\rm{ }}cm\) và biên độ dao động \(A{\rm{ }} = {\rm{ }}4cm\) không đổi khi truyền đi. Gọi \(MN\) là hai điểm trên dây cách nhau một đoạn \(25cm\) theo phương ngang. Tính khoảng cách lớn nhất và nhỏ nhất giữa hai điểm \(MN\) ?
Trả lời bởi giáo viên
Độ lệch pha của M và N là: \(\Delta \varphi = \dfrac{{2\pi {\rm{d}}}}{\lambda } = \dfrac{\pi }{3}\)
Lệch pha về thời gian: \(\Delta t = \dfrac{\pi }{3}.\dfrac{T}{{2\pi }} = \dfrac{T}{6}\)
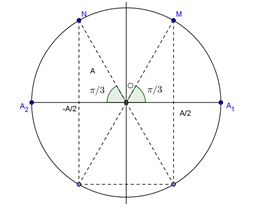
Từ giản đồ Fresnel, ta có: \(\dfrac{A}{2} = \dfrac{a}{2} \Rightarrow A = a\)
Khoảng thời gian ngắn nhất phần tử M tới biên dương là: khoảng thời gian M đi từ \(\dfrac{a}{2}\) đến \(a\):
\(\Delta \varphi = 2\pi - \dfrac{\pi }{3} = \dfrac{{5\pi }}{3} \Rightarrow \Delta t = \dfrac{{5T}}{6}\).
Hướng dẫn giải:
+ Sử dụng biểu thức tính độ lệch pha giữa hai điểm: \(\Delta \varphi = \frac{{2\pi d}}{\lambda }\)
+ Sử dụng biểu thức pha thời gian: \(\Delta \varphi = \omega \Delta t\)
+ Sử dụng giản đồ Fresnel

